Le Lac Blanc, déformations visibles dans les roches et les fossiles (Pralognan-La-Vanoise, Savoie)

Source - © 2022 Théo Marchand

Figure 1. Terrier fossile déformé et reconstitution de sa forme initiale supposée

L'image de gauche présente le fossile de terrier marin tel que trouvé sur le terrain. Le fossile semble avoir été déformé par étirement selon l'axe droite-gauche de l'image. En supposant que le terrier doit avoir une largeur constante tout du long et que l'aire du fossile doit rester la même (déformation à surface constante sur ce plan), on peut proposer une reconstitution de la forme supposée initiale du fossile (image de droite) (voir aussi, plus bas, figure 8).

Localisation par fichier kmz des abords du Lac Blanc, Parc national de la Vanoise, Pralognan-la-Vanoise (Savoie).

L'image de la semaine dernière (cf. Le Lac Blanc, une plage marine de 240 Ma à 2 400 m d'altitude (Vanoise, France)) présentait l'histoire sédimentaire marine du Lac Blanc, un lac de montagne du Parc national de la Vanoise. Aujourd'hui nous allons nous intéresser aux déformations visibles aux abords du Lac Blanc liées à la tectonique des Alpes.

Les déformations les plus évidentes sont les plis visibles sur les affleurements. Deux plis sont particulièrement visibles. Le premier pli en Z à l'échelle décimétrique déforme des structures hétérogènes juste au bord du sentier de randonnée du lac (figures 2 et 3). Le deuxième, d'échelle métrique, déforme des structures calcaires et est également visible depuis le sentier de randonnée (figures 4 et 5). Ces plis indiquent des déformations en raccourcissement, ce qui n'est pas étonnant dans un contexte alpin. Cependant, des déformations extensives peuvent également exister en contexte de chaines de montagnes (Mathey et al., 2021 [4] ; figure 17).

Source - © 2022 Théo Marchand Figure 2. Pli en Z au bord du lac Blanc Ce pli en Z, parfaitement visible sur cet affleurement décimétrique au bord du sentier, témoigne de déformations en raccourcissement peu surprenantes en contexte alpin. La dissymétrie du pli indique une composante cisaillante : dans la configuration actuelle, le haut part vers la droite et le bas vers la gauche. Voir aussi les figures 8 et 9 de Plis dans une zone de convergence (chaîne de collision) : la vallée de Sarchu dans l'Himalaya, Ladakh (Inde).

Source - © 2022 Théo Marchand Figure 3. Pli en Z au bord du Lac Blanc, vue annotée Ce pli en Z, parfaitement visible sur cet affleurement décimétrique au bord du sentier, témoigne de déformations en raccourcissement peu surprenantes en contexte alpin. La dissymétrie du pli indique une composante cisaillante : dans la configuration actuelle, le haut part vers la droite et le bas vers la gauche. Voir aussi les figures 8 et 9 de Plis dans une zone de convergence (chaîne de collision) : la vallée de Sarchu dans l'Himalaya, Ladakh (Inde).

Source - © 2022 Théo Marchand Figure 4. Plis dissymétriques au bord du lac Blanc Un premier pli est visible au centre de l'image. Un deuxième pli est visible au-dessus, mais davantage évident sur la figure 4. Ces plis métriques déforment des dépôts calcaires anisiens et scythiens (tC1 sur la feuille de Modane, voir figures 12 et 15)

Source - © 2022 Théo Marchand Figure 5. Plis dissymétriques au bord du lac Blanc, vu un peu plus large Un premier pli se distingue dans l'ombre, au centre de l'image, mais plus facilement visible sur la figure 4. Un deuxième est bien visible au-dessus. Ces plis témoignent de déformations en raccourcissement.

Dans l'image de la semaine dernière, les déformations ductiles (non cassantes) des structures d'ichnofossiles (fossiles de traces d'êtres vivants, et pas des êtres vivants eux-même) de bioturbation (remaniement du substrat par des organismes vivants) avaient été rapidement évoquées.

Sur la figure 6, on voit un terrier enroulé. Ce terrier semble avoir été allongé dans l'axe droite-gauche de la photographie.

Sur la figure 7, la section visible est perpendiculaire au plan de schistosité. On suppose que ces terriers avaient au départ une section circulaire (cf. Les thalassinoïdes, d'étranges ichnofossiles, et un possible équivalent actuel, les terriers des crabes de mangrove). On voit des sections de terriers, de forme plutôt elliptique avec des grands axes plus ou moins parallèles au plan de schistosité (selon la direction droite-gauche de la photographie) et de petits axes plutôt perpendiculaires au plan de schistosité (selon la direction haut-bas de la photographie).

Source - © 2022 Théo Marchand

Figure 6. Terrier marin fossile déformé, dans les schistes bioturbés du lac Blanc

Ce fossile semble avoir été étiré selon l'axe droite-gauche de l'image. En posant quelques hypothèses de travail, on peut essayer de reconstituer sa forme initiale et d'estimer les axes de déformation se trouvant dans le plan de schistosité (figures 1 et 9, tableau 2).

Source - © 2022 Théo Marchand

Figure 7. Sections déformées de terriers marins, plan de coupe perpendiculaire au plan de schistosité

Différentes sections de terriers marins fossiles sont visibles dans ce plan perpendiculaire au plan de schistosité. La forme globalement elliptique (ou parfois losangique) des sections de terriers supposées initialement circulaires peut s'expliquer de plusieurs façons qui seront discutées par la suite.

L'anneau de porte-clé (flou derrière l'échantillon) donne l'échelle.

Passer d’un cercle à une ellipse… ne pas aller trop vite !

Le passage d'une forme initiale circulaire à une forme finale elliptique est trop intuitivement interprété comme le résultat d'un étirement dans la direction du grand axe de l'ellipse accompagné d'un raccourcissement dans la direction du petit axe. Ceci est un raisonnement hâtif considérant une conservation de la surface de la forme initiale (si on étire dans une direction on doit alors nécessairement raccourcir dans une autre [cas a) sur la figure ci-dessous]) et ne considérant pas la possibilité d'un cisaillement simple (simple shear) pour lequel un cercle aboutit à une ellipse de même surface sans aucun raccourcissement “réel” selon le petit axe (cf. Dequincey et al., 2007 [1]).

De plus, l'hypothèse de conservation de surface, souvent invoquée, n'est généralement qu'un artifice calculatoire dans un cas où l'on ne s'intéresse finalement qu'à une déformation en 2D (on évacue alors la troisième dimension en supposant l'absence de déformation dans cette direction, ce qui permet de passer d'une déformation isovolume en 3D à une déformation à surface constante en 2D).

Source - © 2023 Olivier Dequincey

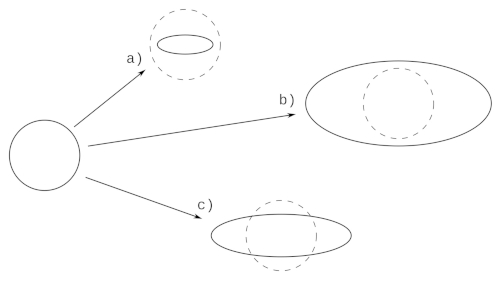
Figure. Déformations d’un cercle aboutissant toutes à une ellipse de grand axe horizontal

Géométriquement parlant, on peut déformer un cercle en une ellipse de grand axe droite-gauche et de petit axe haut-bas de plusieurs manières.

a) Le cercle a été raccourci dans les deux directions, mais moins selon le grand axe. L’aire de l’ellipse est inférieure à celle du disque de départ.

b) Le cercle a été allongé dans les deux directions, mais plus selon le grand axe. L’aire de l’ellipse est supérieure à celle du disque de départ.

c) Le cercle a été raccourci selon le petit axe et allongé selon le grand axe. Selon les facteurs relatifs de raccourcissement et d’allongement, l’aire de l’ellipse peut être supérieure ou inférieure à celle du disque de départ.

Si on prend en compte toutes les possibilités géométriques, un cercle peut devenir une ellipse suite à un étirement selon les directions du grand axe et du petit axe, avec un étirement plus important selon le grand axe [cas b) sur la figure ci-dessus] (et un raccourcissement “compensatoire” dans la troisième dimension en cas de déformation isovolume), ou alors à un raccourcissement selon les directions du grand axe et du petit axe, avec un raccourcissement moins important selon le grand axe [cas c) sur la figure ci-dessus] (et un étirement “compensatoire” dans la troisième dimension en cas de déformation isovolume).

À partir des figures 6 et 7 on peut essayer de caractériser les déformations en 3 dimensions des schistes bioturbés en tentant de reconstruire l'ellipsoïde de déformation, ou plutôt en montrant la démarche à suivre.

Les déformations sont considérées comme homogènes à l'échelle de l'affleurement. Ce qui permet de considérer que ce que l'on voit sur la tranche d'un bloc (figure 7) est bien ce que l'on verrait sur la tranche de la dalle située à proximité (figure 6). Par la suite, les orientations X et Y correspondront au plan de schistosité (plan souvent horizontal sur le terrain) sur lequel on observe le terrier en U (figure 6), et la direction Z sera la direction perpendiculaire à ce plan de schistosité.

On va procéder par étapes en commençant par le plan de schistosité (figure 6), avant d'analyser un plan perpendiculaire (figure 7) en proposant plusieurs approches.

Caractérisation de la déformation dans le plan de schistosité / stratification

Le terrier des figures 1 et 6 semble avoir été “étiré” de manière maximale dans l'axe droite-gauche de la photographie, axe que l'on nommera X (dénomination classique de l'axe d'élongation maximale pour l'ellipsoïde de déformation en 2D ou en 3D). Pour cette approche en 2 dimensions, l'axe haut-bas de cette figure 6 sera nommé axe Y.

Pour estimer ces déformations, on s'appuie sur plusieurs hypothèses raisonnables.

Tout d'abord, on suppose que la photographie a été prise parfaitement face au plan visible, de manière à ce qu'il n'y ait pas d'effet de perspective. Cette hypothèse est discutable puisque la photographie n'a pas été prise en laboratoire, mais on s'en contentera pour une estimation grossière dont le but est aussi de montrer la démarche.

On suppose ensuite que le terrier originel avait initialement la même largeur tout du long comme c'est le cas de nombres de terriers actuels et de terriers fossiles sur des surfaces non déformées. On suppose aussi que le terrier était bien dans le plan de stratification et que la schistosité actuelle est parallèle à l'ancienne stratification, et donc qu'il n'y a pas de biais de coupe. Le fait que la déformation semble homogène tout au long du terrier (amincissement maximal en bas et élargissement maximal sur les côtés) laisse espérer que cela est le cas.

On considère aussi, en l'absence de traces évidente du contraire, que la déformation s'est produite à volume constant (ni perte – dissolution et export – ni gain – apport et cristallisation – de matière).

Enfin, pour ce premier calcul sur le plan XY, on suppose l'absence de déformation perpendiculairement à ce plan, ce qui revient à considérer ici une déformation à surface constante sur le plan de schistosité / stratification. On rediscutera cette dernière hypothèse “calculatoire” par la suite, puisque cette dernière hypothèse suppose qu'il n'y a ni étirement ni raccourcissement dans la direction Z alors qu'on va par la suite s'intéresser à la possible déformation selon cette direction.

Pour le terrier vu sur le plan de schistosité (figure 8), la première étape est de déformer l'image jusqu'à obtenir une forme de largeur constante (terrier de largeur constante). Il faut ensuite agrandir (ou rétrécir selon comment on a précédemment déformé l'image) l'image du fossile, en conservant les proportions de l'image, afin que l'aire du terrier fossile déformé (tel que trouvé sur le terrain) soit égale à l'aire du terrier originel reconstitué. Le logiciel Inkscape est très pratique pour détourer les images et mesurer leurs surfaces. Les aires obtenues sont presque égales à 0,2 % près, on considèrera donc que l'influence sur l'estimation des élongations est minime (tableau 1).

Source - © 2022 Théo Marchand

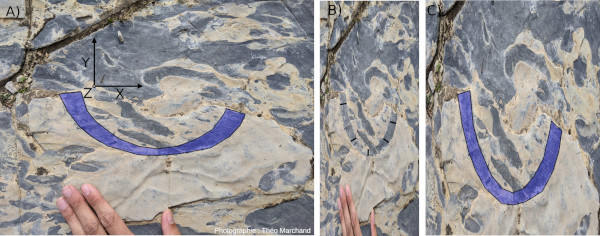
Figure 8. Reconstitution de la forme supposée initiale du terrier fossile de la figure 7

La reconstitution s'est faite en 2 étapes. La forme actuelle (A) a été délimitée en bleu. L'image a ensuite été écrasée sur un côté (axe droite – gauche) afin que la forme fossile ait la même largeur tout du long ; sur le panneau B, les traits noirs ont tous la même longueur, afin de souligner l'homogénéité de largeur du terrier sur l'image obtenue. Enfin (C), l'image a été agrandie en conservant ses proportions, jusqu'à ce que la forme délimitée en bleu ait la même aire que la forme initiale (hypothèse de calcul).

Les valeurs estimées sont donc f_X=1,78 et f_Y=0,56.

Caractérisation de la déformation dans le plan normal à la schistosité / stratification

– Cas d'un aplatissement selon Z (cisaillement pur ou pure shear)

Les sections de terrier visibles sur la figure 7 peuvent sembler avoir été aplaties selon l'axe Z normal au plan de schistosité, et allongées dans ce plan de schistosité. Cet aplatissement, s'il existe réellement, pourrait être dû en partie ou en totalité au poids des sédiments s'accumulant, c'est-à-dire à la contrainte lithostatique, qui n'est pas isotrope près de la surface, mais l'est de plus en plus avec la profondeur.

Tentons de quantifier la déformation dans le plan perpendiculaire au plan de schistosité en considérant qu'il s'agit d'un simple aplatissement appelé aussi cisaillement pur (pure schear) [1].

On considère comme précédemment que l'éventuel effet de perspective de la photographie est limité.

Pour le calcul, on va considérer que les ellipses observées étaient à l'origine des disques correspondant à la section des terriers. Mais puisqu'aucune orientation préférentielle des fossiles n'a été observée (cf. Le Lac Blanc, une plage marine de 240 Ma à 2 400 m d'altitude (Vanoise, France)), il est illusoire de penser qu'une coupe “au hasard” permettra de visualiser systématiquement des sections originellement circulaires. Sachant qu'un tube de section circulaire coupé de biais donne déjà une ellipse, le fait de revenir, par le calcul, à un disque plutôt qu'à une ellipse moins déformée aboutit à surestimer la déformation subie. On va donc effectuer les calculs sur les sections utilisables et ne conserver que la plus faible valeur de déformation, laquelle sera soit, par chance, la déformation réelle dans le plan de coupe, soit, du moins, la moins surestimée. On nommera L la direction perpendiculaire à Z dans ce plan de coupe.

On va une fois de plus partir sur une hypothèse de déformation isovolume et considérer une déformation à surface constante dans le plan de coupe, même si cela n'est pas “logique”. En effet, dans le calcul précédent de f_X et f_Y, on a fait la même hypothèse impliquant une absence de déformation selon l'axe Z (f_Z=1), déformation que l'on tente maintenant de déterminer. On verra en quoi ces hypothèse contradictoires ne sont en fait qu'un subterfuge calculatoire temporaire.

Source - © 2022 Théo Marchand

Figure 9. Mesure des sections de quelques terriers, perpendiculairement au plan de schistosité

Les 4 sections les plus visibles et identifiables ont été sélectionnées. Les grands axes (à peu près horizontaux) ont été délimités en noir, et les petits axes ont été délimités en rouge. Les longueurs des axes ont été mesurées en pixels, sur l'image, et reportés dans le tableau 2.

En gardant la déformation la plus faible (facteurs d'élongation les plus proches de 1) on a f_Z=0,50 et f_L=2,00. Données à ajouter aux résultats précédents : f_X=1,78 et f_Y=0,56.

Rendu à ce point, on doit remarquer plusieurs soucis apparents ou réels.

Tout d'abord on a un facteur d'élongation f_L supérieur au facteur d'élongation maximal f_X. Ceci est simplement dû au fait que les calculs dans les plans XY et ZL ont été menés à surface constante dans chacun des plans (le facteur d'élongation perpendiculaire au plan étudié est alors supposé égal à 1). En faisant cela, on ne trouve pas les facteurs d'élongations “absolus” mais “relatifs” puisqu'on suppose en réalité qu'il y a quand même déformation dans la direction perpendiculaire au plan étudié. Ainsi, en réalité on a vraiment f_X=1,78/0,56f_Y (soit f_X=3,18.f_Y) et f_Z=0,50/2,00.f_L (soit f_Z=0,25.f_L).

Ensuite, il nous manque une équation pour résoudre le système f_X-f_Y-f_Z , car le calcul sur le plan ZL introduit un quatrième terme, f_L, plutôt que de nous donner une troisième relation entre les 3 facteurs d'élongation principaux. Pour cela, il nous manque la connaissance de la direction L sur le plan XY. En effet, par construction, connaissant les directions X et Y et les facteurs f_X et f_Y, le facteur f_L correspond au “rayon” de direction L de l'ellipse de demi-grand axe f_X et de demi-petit axe f_Y (calcul “simple” nécessitant de connaitre l'angle entre les directions X et L). Ainsi, on aurait une relation entre f_L et les facteurs f_X et f_Y permettant d'obtenir une relation entre f_Y et les facteurs f_X et f_Y. À partir des deux relations “calculées” et de l'équation liée à l'hypothèse “isovolume”, on obtiendrait finalement les 3 facteurs d'élongation désirés.

Limitation supplémentaire, ici, on n'a pas de mesures de terrain de quelques longueurs, sections, axes qui permettraient par exemple de comparer rapidement le diamètre du terrier déformé selon les axes X, Y et Z ce qui ôterait toute hésitation concernant les directions de déformation minimale, intermédiaire et maximale… en supposant tout de même que tous les terriers ont initialement une section comparable.

– Cas d'un simple cisaillement parallèle à XY (cisaillement simple ou simple shear)

Mais on peut aussi regarder de plus près la vue par la tranche et proposer une autre approche, celle d'un cisaillement comme déjà évoqué par l'observation de plis dissymétriques (figures 2 et 3).

On observe en effet sur la vue par la tranche, non seulement des plans de schistosité mais aussi ce qui semble pouvoir être des plans de cisaillement. Le fait que les axes de déformations identifiés dans les quasi-ellipses de la figure précédente (figure 9) ne sont pas exactement verticaux et horizontaux s'expliquerait alors par l'existence d'un “vrai” ou “simple” cisaillement (simple shear) [1]. Dans ce cas, une section circulaire est transformée en ellipse sans aucun aplatissement vertical mais par un simple mouvement relatif de cisaillement avec, ici, le haut allant vers la droite et la base vers la gauche (cisaillement dextre sur la photographie), avec conservation de la surface.

Source - © 2022 Théo Marchand

Figure 10. Plans de schistosité (en rouge) et plans de cisaillement (en noir) affectant les terriers fossiles vus par la tranche

Les plans de cisaillement les plus évidents ont été soulignés en noir.

Ellipsoïde de déformation des calcaires bioturbés

Si on considère que la déformation dans le plan de coupe ZL (figures 6, 9, 10) est un cisaillement simple (simple shear), alors f_Z=1 et donc f_X=1,78 et f_Y=0,56. Remarquons que, dans ce cas, on peut déterminer le diamètre initial des terriers (c'est la “hauteur” selon l'axe Z des terriers déformés, la distance verticale entre le point le plus haut et le point le plus bas du terrier déformé).

Si on reste sur l'idée initiale d'un aplatissement (pure shear) alors, on l'a vu, les données de terrains sont insuffisantes pour déterminer l'aplatissement selon Z et l'ellipsoïde de déformation avec précision.

Outre ces deux cas extrêmes, on pourrait avoir un cisaillement avec aplatissement auquel cas on pourrait alors, sauf données de terrain supplémentaires non abordées ici, tenter de déterminer des ellipsoïdes de déformation extrêmes, la déformation réelle étant entre les deux.

Plis et failles majeurs à l'échelle du paysage (et de la carte géologique)

Certaines déformations sont identifiables à l'échelle du paysage, grâce à une analyse plus poussée des roches à l'affleurement et grâce à la feuille géologique de Modane [5].

Avant d’arriver au refuge de Péclet-Polset et au Lac Blanc, le sentier de randonnée en provenance du parking des Prioux (chemin le plus direct depuis Pralognan-La-Vanoise) passe en contrebas d’une imposante barre rocheuse calcaire de quelques dizaines de mètres de puissance. Les ichnofossiles de bioturbation font partie de cet ensemble calcaire, situés au sommet. L’étude de la feuille géologique de Modane à 1/50 000 [5] permet de constater que, de manière surprenante, les terrains les plus jeunes (tC3 : Anisien supérieur à Ladinien inférieur) sont ici situés à la base de la série, et les couches les plus anciennes (tC1 : Anisien inférieur et Scythien supérieur) sont situées au-dessus. On a donc une stratification inverse de cet ensemble qui s’explique par un pli décrit dans la notice de la carte géologique comme l’« anticlinal couché du Lac Blanc ». La stratification inverse est indiquée sur la carte par le symbole .

La présence d'une faille est également indiquée sur la carte, le long du chemin de randonnée entre le refuge de Péclet-Polset et le Lac Blanc. À cet endroit, on a un contact entre des calcaires triasiques et des roches plus anciennes (h5-r : Stéphanien à Stéphano-Permien). Le fait que le Stéphanien soit directement au contact des calcaires triasiques indique qu’une partie des terrains intermédiaires (les gneiss du Sapey notés G sur la figure 14) a “disparu à cause d’une faille. Cette faille est en large partie invisible, comme indiqué par le figuré en pointillés (figures 13 et 16).

Source - © 2022 Théo Marchand Figure 11. Barre rocheuse calcaire du Lac Blanc, à stratification inverse Cette barre rocheuse située au-dessus du sentier de randonnée qui permet l'accès au refuge de Péclet-Polset présente une stratification inverse : les terrains les plus jeunes sont en-dessous et vice versa. Cette disposition surprenante résulte d'un pli couché (figures 13 à 16). La stratification inverse n'est pas visible par le paysage. Son identification doit se faire (1) par l'observation d'un pli couché, ou (2) par la datation (ici, relative) des différentes couches.

Source - © 2022 Théo Marchand Figure 12. Barre rocheuse calcaire du Lac Blanc, à stratification inverse Le refuge de Péclet-Polset est visible à gauche de l'image. Les terrains visibles à droite sont surtout de l'Anisien moyen (tC2 sur la feuille de Modane). La stratification inverse de cette barre rocheuse indique un pli couché (figures 13 à 16).

Source - © 2023 D’après BRGM / InfoTerre

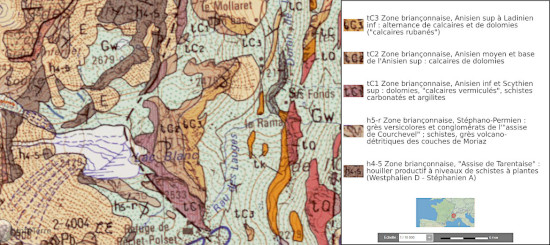
Figure 13. Extrait de la feuille géologique de Modane à 1/50 000 montrant le Lac Blanc et ses environs

Le Lac Blanc est présent au centre, légèrement au Nord du refuge de Péclet-Polset. La barre rocheuse à stratification inverse est constituée de terrains de l'Anisien (tC1, tC2, tC3). Le symbole au-dessus de la légende “Lac Blanc” indique qu'il s'agit d'une stratification inverse. Au contact des terrains tC1, on trouve également le figuré “faille” en pointillé, indiquant que la faille est la plupart du temps supposée mais non visible car recouverte par des dépôts plus récents. Cette faille sépare les terrains calcaires triasiques, du Stéphanien (h4-5 au Nord, et h5-r au Sud).

Source - © 1989 Notice de la feuille géologique de Modane à 1/50 000 [5]

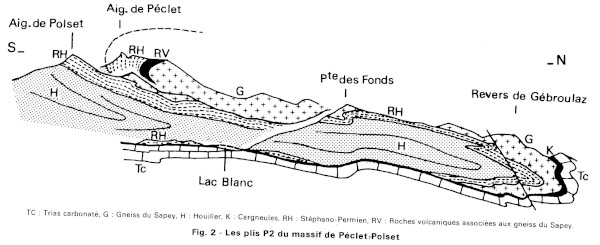
Figure 14. Coupe géologique présentant l'anticlinal couché du Lac Blanc

La position du Lac Blanc est indiquée sur la coupe. Les calcaires triasiques sont indiqués par le figuré “en pavés blancs” (Tc). Le cœur du pli est constitué des formations houillères (gris, H) et du Stéphano-Permien (tiretés, RH). Les terrains les plus anciens sont donc au cœur du pli : il s'agit donc bien d'un anticlinal. Un synclinal, également couché, est représenté sur la partie supérieure gauche, au niveau de l'Aiguille de Péclet.

Source - © 2023 D’après Google Earth Figure 15. Vue satellite du Lac Blanc et de la barre calcaire à stratification inverse La stratification inverse n'est pas visible par le paysage. Son identification doit se faire (1) par l'observation d'un pli couché, ou (2) par la datation (ici, relative) des différentes couches.

Source - © 2023 D’après BRGM / Google Earth Figure 16. Vue du Lac Blanc avec projection de la feuille géologique de Modane au 1/50 000 Cette vue correspond exactement à celle de la figure précédente. Le symbole indique que les terrains calcaires sont en stratification inverse.

Conclusion

La démarche de reconstruction de l'ellipsoïde de déformation a permis de travailler sur plusieurs aspects et plusieurs hypothèses classiques quand on travaille sur les déformations géologiques (déformation à volume constant, formules d'élongation et de facteur d'élongation, aplatissement, cisaillement). Toutes les déformations présentées témoignent de raccourcissements à l’échelle régionale (plis, faille inverse) qui ne sont pas surprenantes dans l'histoire tectonique des Alpes. Cependant, les contraintes tectoniques compressives sont actuellement minoritaires dans les Alpes (Mathey et al., 2021 [4], figure 17).

Source - © 2021 D’après Mathey et al. [4], CC BY 4.0

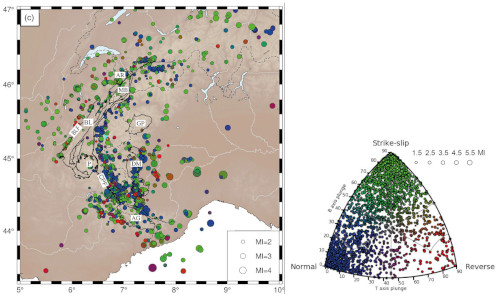
Figure 17. Contraintes tectoniques actuelles dans les Alpes

L'étude a compilé 2 215 mécanismes au foyer dans les Alpes. MI est la magnitude des séismes. Les sphères inverses (contraintes compressives) sont dans les tons rouges, les sphères normales (extensives) sont en bleu et les décrochements (strike-slip) sont en vert. Les mécanismes compressifs sont actuellement minoritaires dans les Alpes.

L'emplacement approximatif du lac Blanc est indiqué par une croix bleu clair (rajoutée sur la figure originale).

Pour rappel, estimer l'ellipsoïde de déformation est bien plus simple quand on a au départ un objet 3D sphérique (oolite, radiolaire …), ou circulaire si on raisonne en 2D. D'autres exemples ont déjà été abordés sur Planet-Terre, par exemple dans Oolites déformées, Plan d'aplatissement, plans de schistosité (plans S) et plans de cisaillement (plans C), Ammonite déformée dans les marnes du Jurassique inférieur de Champ sur Drac (Isère) ou encore Trilobites déformés.