Article | 16/06/2000
Augmentation du CO2 atmosphérique au cours des derniers siècles
16/06/2000
Auteur(s) / Autrice(s) :
Publié par :
- Benoît UrgelliENS de Lyon / DGESCO
Résumé
TD 3/3 sur le cycle du carbone. Bilan de carbone dans le système atmosphère-océan-biosphère depuis la période pré-industrielle, problèmes liés à la conférence Kyoto...
Le carbone atmosphérique depuis la période pré-industrielle
Le dioxyde de carbone est mesuré dans l'atmosphère depuis une cinquantaine d'années. Un américain, C. Keeling, est le premier à avoir systématiquement mesuré ce gaz pour suivre son évolution, à Hawaii, dès les années 50. Mais déjà en 1896, S. Arrhenius, un scientifique suédois, observe que la pression partielle de ce gaz augmente dans l'atmosphère et que cette augmentation pourrait être à l'origine d'une hausse de la température du globe.
Pour remonter avant 1950, on mesure ce gaz dans les bulles d'air des calottes polaires. En effet, après son dépôt au sommet de la calotte, la neige se transforme en glace. Cette glace va piéger des bulles de gaz entre ses cristaux, et la mesure de la composition de ces bulles d'air témoigne de la composition de l'atmosphère libre au moment de l'isolement de ces bulles.
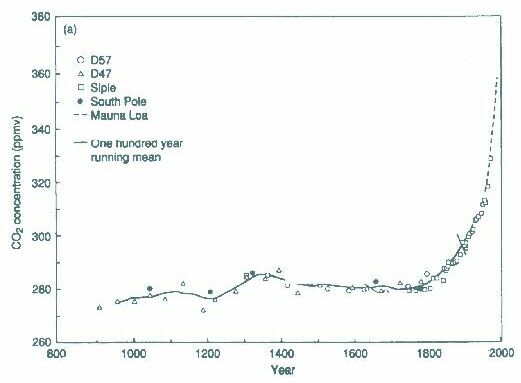
Cette courbe a été construite grâce aux mesures directes dans l'atmosphère et aux enregistrements dans les glaces des calottes polaires.
Q1 : Comment expliquer l'augmentation du CO2 atmosphérique ?
La pression partielle de CO2 a pu être mesurée au Pôle Sud dans les bulles d'air des carottes de glace. En comparant les valeurs de CO2 au Pôle Sud et à Hawaii (Mauna Loa), C.Keeling a constaté qu'il existait un gradient interhémisphérique.
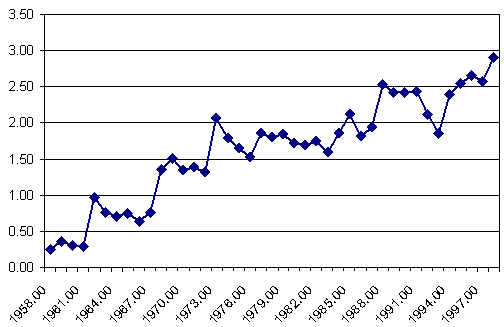
Q2 : Commentez la variation et le signe de ce gradient et proposez une explication.
Depuis les débuts de l'industrialisation, les hommes brûlent charbon, pétrole et gaz naturel
Cette consommation de « carbone fossile » ou « fossil fuel » produit du dioxyde de carbone qui est injecté dans l'atmosphère. Durant la période 1860-1990 on estime que 230,02453 GtC ont été libérées dans l'atmosphère (estimations d'injection de carbone, en Gt de C par an, dans l'atmosphère par combustion des combustibles fossiles (pdf) ou (ods)).
Parallèlement, les modifications d'utilisation des sols et la déforestation ont également contribué à injecter du carbone dans l'atmosphère. Les estimations sont ici plus difficiles, mais sont estimées à 121,8475 GtC entre 1860 et 1990.
Q2 : Quelle serait l'augmentation du CO2 atmosphérique en 1990 correspondant à l'injection du carbone fossile et du carbone provenant de la déforestation de 1860 à 1990 ?
Données : Masse molaire du carbone 12 g/mol, Volume molaire 22,4 l/mol ; Volume de la troposphère : rayon de la terre 6 400 km, hauteur de la troposphère : 7-8 km.
Q4 : Comparer cette valeur avec celle qui est mesurée dans l'atmosphère (voir première figure du TD). Comment expliquer la différence ?
Puits biosphériques et océaniques pour la décennie 80
Plusieurs méthodes ont été utilisées par les scientifiques pour séparer les puits biosphériques et océaniques pour la décennie 80.
a) Des modèles du cycle du carbone océanique (voir TD 2) peuvent donner une estimation du puits océanique. Une estimation de ce puits peut également être obtenue à partir de mesures de pCO2 dissous dans les eaux de surface de l'océan et de mesures de l'intensité du vent. Une valeur moyenne du puits océanique pour la période 80-89 est estimée à 2 GtC/an (IPCC, 95).
Q5 : En utilisant cette valeur et celle qui sont vous sont données précédemment, proposez un bilan complet du carbone (source et puits) pour la période 80-89.
b) Pour déterminer les puits biosphérique et océanique sans utiliser de modèles, une autre méthode a été proposée (Keeling et al., 92, 96, Battle et al. 2000). Elle consiste à introduire une deuxième équation (la première étant celle du bilan de carbone, contenant deux inconnues, les puits océanique et biosphérique). Cette deuxième équation représente le bilan d'oxygène. On s'intéresse ici à la période 90-97.
Plusieurs hypothèses et données sont nécessaires pour traiter le problème :
Pour la photosynthèse, 1,1 mol d'O2 sont produite pour chaque mole de CO2 qui rentre dans la biosphère.
Pour la combustion des combustibles fossiles, 1,43 mol d'O2 sont utilisées pour la libération d'une mole de CO2. On suppose que pour cette période 6,2 GtC sont libérées chaque année.
On suppose que les échanges nets océanique d'oxygène sont nuls sur la période considérée.
Enfin, les mesures atmosphériques montrent pour la période considérée :
Une augmentation du CO2 atmosphérique moyenne de 1,25 ppm/an.
Une diminution de l'oxygène de 16 per meg/an. (à stoechiométrie égale, 4,18 per meg d'O2 correspondent à 1 ppm de CO2).
Q6 : Pour trouver les puits océanique et biosphérique moyen sur cette période, proposez :
une méthode graphique
une résolution du système de 2 équations à deux inconnus.
Variation locale et saisonnière du CO2 atmosphérique
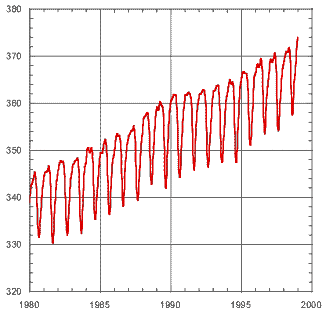
Q7 : Comment expliquer les différentes variations que vous observez sur cette courbe ?
On vous donne ici les mesures de CO2 atmosphérique (1, 2, 3) pour trois stations (A : Point Barrow (Alaska), B : Mauna Loa (Hawaii), en altitude., C : South Pole (Antarctique))
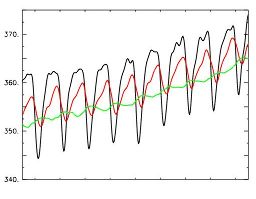
Vert : station 1, Noir : station 2, Rouge : station 3.
Q8 : A vous de retrouver la courbe qui appartient à chaque station et d'expliquer les raisons de votre choix.
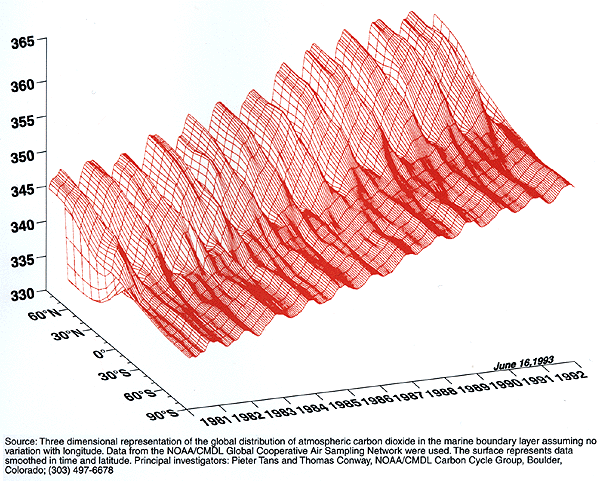
Cette figure est appelée « flying carpet » ou « tapis volant » par les scientifiques.
Q9 : Commentez les principales caractéristiques de la figure ci-dessus.


