Trilobites déformés

Source - © 2002 Pierre Thomas

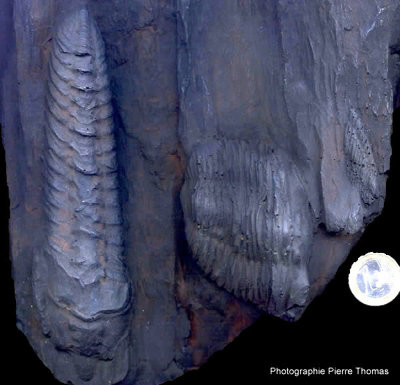
Figure 1. Fossiles de trilobites du Silurien

Deux fossiles de trilobites du Silurien ayant subi une déformation au Carbonifère moyen.

Au Silurien, en Bretagne, deux trilobites (Calymènes) sont morts, et le hasard a fait en sorte que leur cadavres soient disposés perpendiculairement l'un de l'autre. Ils se fossilisèrent ensuite dans cette position.

Au Carbonifère moyen, la tectonique hercynienne entraina un raccourcissement droite-gauche, et donc un étirement bas-haut (dans la position de la photo). Bien entendu, la déformation s'est faite à volume (et surface) constante. Du fait du sens cette déformation unique mais des deux orientations perpendiculaires initiales des fossiles, le trilobite de gauche s'est allongé et aminci, alors que celui de droite s'est raccourci et élargi.

Complément de janvier 2023.

Petit exemple d’estimation de déformation. À partir de cette image, on peut tenter d’estimer l’allongement et le raccourcissement subis. On va d’abord supposer qu’il n’y a pas de changement (ni allongement, ni raccourcissement) perpendiculairement au plan de l’échantillon (les trilobites ne semblent en effet ni écrasés, ni étirés perpendiculairement à la plaque de l’échantillon). On considère aussi que la déformation s’est produite à volume constant (ni perte, ni apport de matière) et donc que la déformation s’est produite à surface constante pour la photographie, puisque la déformation est supposée nulle perpendiculairement à la plaque. De ce fait, la surface étant constante, le facteur d’allongement est l’inverse du facteur de raccourcissement. Il est essentielle de connaitre ou du moins d’estimer l’état initial (on n’a ici que l’état déformé). Les fossiles de Calymènes montrent généralement un rapport longueur sur largeur de l’ordre de 2. On part donc de cette donnée pour calculer le facteur “x” d’allongement (le raccourcissement est alors 1/x).

Sur l’échantillon on trouve que le trilobite étiré à une longueur “a” de l’ordre de quatre fois sa largeur “4a”. Comme le trilobite initial a des dimensions de longueur 2L et de largeur L (2 fois plus long que large), la conservation de la surface nous permet d’écrire que : L×2L = a×4a soit 2L² = 4a²donc, en divisant chaque membre par 2, L² = 2a². Or, on sait que le facteur de raccourcissement est de 1/x donc que a=L/x d’où L² = 2L²/x², soit 1 = 2/x² ou encore x² = 2 ce qui donne finalement x = √2 ~ 1,414.

Source - © 2002 Pierre Thomas

Figure 2. Estimation du facteur d’allongement / raccourcissement des trilobites

Dans son état initial le trilobite est supposé être 2 fois plus long que large. La déformation étant considérée à surface constante (pas de déformation perpendiculairement à la photo), le facteur d’allongement est de √2 et le facteur de raccourcissement de 1/√2.