Article | 18/10/2019
Le nombre de Rayleigh : une approche “avec les mains”
18/10/2019
Résumé
Conduction et convection, comprendre les paramètres entrant dans l'expression du nombre de Rayleigh. Nombre sans dimension, valeur critique empirique, et application au manteau terrestre.
Table des matières
Formule et paramètres
La formule du nombre de Rayleigh est la suivante.
Équation 1. Le nombre de Rayleigh
Passons en revue les différents paramètres qui apparaissent dans la détermination de la valeur de Ra pour un milieu de nature et de dimension données.
- (alpha) est le coefficient de dilatation thermique volumique. Il quantifie la propension du milieu à se dilater [contracter] lorsque la température augmente [diminue], et s'exprime en K−1.
- (delta T) est la différence de température aux limites du système considéré, et s'exprime en K.
- est l'accélération de la pesanteur régnant dans le système, et s'exprime en m.s−2.
- est la longueur caractéristique du système (par exemple, la hauteur de la couche aux limites de laquelle est mesurée la différence de température ), et s'exprime en m.
- (kappa) est la diffusivité thermique du milieu. Elle quantifie la capacité à transmettre l'énergie thermique d'un point à un autre (paramètre mêlant la conductivité thermique et la capacité calorifique du matériau), et s'exprime en m2.s−1.
- (nu) est la viscosité cinématique du milieu. Elle quantifie la capacité d'un matériau à résister à l'écoulement, au fluage (une faible viscosité indique un écoulement facile), et s'exprime en m2.s−1.
On trouvera des expressions avec d'autres “lettres” possibles, certains paramètres ayant plusieurs écritures “classiques”. Il est donc toujours important de bien savoir à quoi correspond chaque terme lorsqu'on “apprend une formule”.
En prenant en compte l'égalité , on trouve aussi l'écriture : , avec (êta) la viscosité dynamique (en Pa.s) et (rho) la masse volumique (en kg.m−3). Par souci de cohérence on doit alors utiliser pour le transfert thermique la conductivité thermique (en W.m−1.K−1) reliée à la diffusivité par la relation avec la capacité thermique massique du milieu (en J.kg−1.K−1), afin de faire “sortir” des deux paramètres du dénominateur et travailler avec des grandeurs exprimant des énergies et non plus des diffusivités. On obtient alors l'écriture .
Une analyse dimensionnelle montre que le nombre de Rayleigh est bien un nombre sans dimension (sans unité). Ce nombre est en fait le produit de deux nombres, nombre de Grashof (noté Gr) et nombre de Prandtl (noté Pr), eux aussi sans dimension, utilisés pour caractériser la “facilité” / l'“efficacité” relative de la convection et de la conduction comme mode de transfert thermique : . Le nombre de Grashof est le rapport des forces de gravité sur les forces visqueuses () : il quantifie le transfert thermique par déplacement de matière, plus il est élevé, plus la convection est “efficace”. Le nombre de Prandtl () quantifie la rapidité relative d'un milieu à transférer de l'énergie par mouvement de matière (convection) ou par transfert thermique de proche en proche (conduction) ; plus il est élevé, plus les mouvements de matière (convection) expliquent les profils de température du milieu. Il en découle pour Ra, que plus Ra est élevé, plus la convection est “favorisée”.
Empiriquement, par l'étude de systèmes réels variés, on a déterminé une valeur critique au-delà de laquelle le système considéré évacue sa chaleur par convection et non plus par conduction : la valeur de 1700 est souvent trouvée dans la littérature (plus rarement 1000, parfois 2000).
Effet des paramètres sur les forces et échanges thermiques en jeu, valeur critique
Voyons paramètre par paramètre, “avec les mains”, comment, au final, chacun favorise ou limite la convection par rapport à la conduction. Pour cela, on se pose la question de l'effet du paramètre sur l'efficacité à dissiper une petite anomalie thermique (en pensant aux forces en jeu – poids, poussée d'Archimède, résistance – et à la persistance de l'anomalie thermique dans le temps).
Prenons l'exemple d'une anomalie thermique locale affectant un volume initial V de masse M.
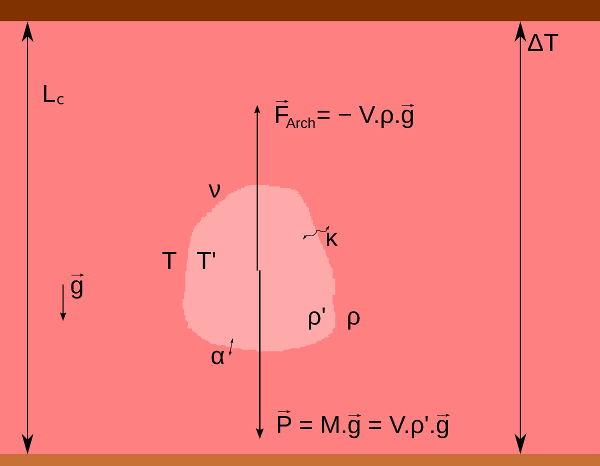
Figure 1. Schéma d'une anomalie thermique locale et paramètres du nombre de Rayleigh
Une anomalie thermique de volume V et de masse M est soumise à son poids et à une poussée d'Archimède. Les caractéristiques physiques, les forces subies et la stabilité temporelle dépendent de la température et des paramètres du milieu.
Ce schéma correspond à un système qui ne montre pas de production interne de chaleur. Pour le manteau terrestre, par exemple, la production interne de chaleur implique un calcul un peu différent du paramètre , mais les paramètres physiques à prendre en compte reste inchangés.
Plus le coefficient de dilatation thermique volumique est élevé, plus l'anomalie thermique subit une variation de volume importante pour un écart de température donné. La masse de l'anomalie thermique est inchangée et donc son poids ne varie pas. Mais la poussée d'Archimède, égale au “poids de liquide déplacé”, est fonction du volume : “volume × masse volumique du milieu non perturbé × ”. Plus est grand, plus la variation de volume engendrée est importante, plus l'effet sur la poussée d'Archimède est important. En cas d'anomalie “chaude”, la dilatation importante entraine une augmentation de la poussée d'Archimède à poids égal et favorise donc un mouvement de convection ascendant. À l'inverse, en cas d'anomalie froide, la contraction réduit fortement la poussée d'Archimède et favorise par conséquent un mouvement de convection descendant, le poids étant,lui, inchangé. Ainsi, une augmentation du coefficient de dilatation thermique volumique favorise les mouvements de matière, c'est-à-dire la convection.
L'accélération de la pesanteur intervient dans l'expression des forces tendant à mettre en mouvement la matière : poids et poussée d'Archimède. Plus est élevé, plus ces forces sont importantes et donc, surtout, plus la force résultante tendant à faire remonter ou plonger la matière est importante. Il en découle qu'une augmentation de l'accélération de la pesanteurfavorise, elle aussi, les mouvements de matière, c'est-à-dire la convection.
Lorsque la diffusivité thermique augmente, cela signifie que le milieu transfère plus facilement, plus rapidement la chaleur par conduction, ce qui a pour conséquence de dissiper plus rapidement toute anomalie locale de température par simple conduction. Les anomalies thermiques sont alors moins longuement intenses, les mouvements de matière ont donc moins de temps pour se mettre en place avant dissipation de l'anomalie par conduction. Autrement dit, une augmentation de la diffusivité thermiquefavorise la conduction.
Lorsque la viscosité cinématique augmente, le milieu résiste plus au mouvement, au fluage. Les mouvements de matière étant freinés, la dissipation des anomalies thermiques par conduction est alors favorisée. Une augmentation de la viscosité cinématiquefavorise donc la conduction.
L'écart de température intervient de concert avec la dilatation thermique volumique, c'est le produit qui représente la variation relative de volume. Lorsque augmente, la variation de volume de l'anomalie thermique augmente et, donc, comme pour , une augmentation de la différence de températurefavorise les mouvements de matière, c'est-à-dire la convection.
La longueur caractéristique du système est plus difficile à aborder “avec les mains”. On peut passer cet écueil en invoquant l'usage d'un nombre sans dimension, Ra, et donc la nécessité de faire intervenir une longueur à la puissance 3 pour que le nombre de Rayleigh soit sans dimension, la seule “longueur” définissant le système étant l'épaisseur du système convectif . Plus précisément, on peut dire que la convection a besoin de “place” pour s'exprimer, la taille du système (et même son volume,) serait alors un facteur favorisant la convection, apparaissant donc au numérateur. Une autre manière, est de présenter le nombre de Rayleigh comme le rapport, toujours sans dimension, des temps caractéristiques de mise en place des phénomènes de dissipation des anomalies thermiques que nous noterons temps de diffusion thermique, temps de résistance à l'écoulement, et temps de mise en place de la convection. Ces phénomènes affectant l'ensemble du système, est prise comme dimension représentative de ce système. En ce qui concerne et , ces paramètres expriment des diffusivités, respectivement thermique et de quantité de mouvement, concernant une “surface” par “unité de temps”, en rapportant cela à la “surface caractéristique” par ”temps caractéristique” on écrit alors : et . Les “forces de convection”, , ont la dimension d'une accélération, soit une longueur par unité de temps au carré, soit, une “longueur caractéristique” par “temps caractéristique de convection au carré”, d'où l'expression . Ainsi, lorsqu'on compare les temps caractéristiques de mise en place des phénomènes favorisant la conduction, et au temps caractéristique de mise en place de la conduction, , en gardant un nombre sans dimension, au écrit . La convection se met en place si le “temps” de résistance à la convection est bien plus grand que le “temps” de mise en place de la convection, c'est-à-dire si . En utilisant les égalités précédentes faisant intervenir dans l'expression des temps caractéristiques, on se rend compte que la longueur caractéristique augmente toujours les temps caractéristiques mais pas avec la même “efficacité” et que le rapport des temps caractéristiques fait apparaitre au numérateur (et au cube) ; ce qui montre qu'une augmentation de la longueur caractéristique du systèmefavorise au final la convection.
La valeur critique permettant de considérer que le milieu est convectif est une valeur empirique, ce qui signifie qu'elle a été déterminée par l'étude de différents systèmes conductifs, convectifs et/ou de systèmes contrôlés dont on fait varier certains paramètres pour repérer quand il passe d'un mode de transfert thermique à un autre. Cette valeur critique n'est pas le résultat de calculs théoriques de dynamique des fluides, elle ne découle pas de l'application d'une loi physique, mais est le résultat d'observations et mesures expérimentales qui ont permis de déterminer la valeur de pour laquelle les systèmes basculent de la conduction à la convection.
Le cas du manteau terrestre
Pour tester le caractère globalement conductif ou convectif du manteau, on détermine un ordre de grandeur du nombre de Rayleigh pour ce milieu grâce aux apports de différents types d'études.
À partir d'échantillons de péridotite, on peut mesurer le coefficient de dilatation thermique volumique et la diffusivité thermique de ce matériau dans une large gamme de pression et de température.
Les études sismiques et minéralogiques (transitions de phases) permettent la construction d'un modèle de Terre pour lequel on connait alors l'épaisseur des couches (donc ), la répartition des masses (donc à la surface mais aussi en tout point de l'intérieur de la Terre), et le géotherme moyen (donc un ordre de grandeur de , même si pour le manteau, le chauffage interne par la radioactivité induit un calcul un peu différent du nombre de Rayleigh et de ce que représente ).
La viscosité du manteau est plus difficile à déterminer sur de petits échantillons à placer dans des conditions proches de celles du manteau. Une approche de la viscosité moyenne du manteau, au moins supérieur, est obtenue grâce à la détermination de vitesse de rééquilibrage isostatique suite à la fonte des glaciers d'Europe du Nord depuis 20 000 ans, voir, par exemple, à ce propos Les plages soulevées de Scandinavie et du Canada, conséquences du rebond post-glaciaire. On obtient alors, pour le manteau supérieur asthénosphérique, une viscosité dynamique de l'ordre de 1019 à 1020 Pa.s, soit une viscosité cinématique de l'ordre de 3.1015 à 3.1016 m.s−2 dans ce cas. D'autres études et modèles, voir les données présentées dans Les discontinuités dans le manteau terrestre, ou La convection mantellique, mythes, réalités et questions, ou La convection mantellique, moteur de la tectonique des plaques, si souvent évoquée, si souvent mal comprise… montrent de plus que le manteau inférieur est plus visqueux que le manteau supérieur (d'environ un ordre de grandeur).
La prise en compte des différents paramètres et de leur gamme de valeurs mesurées/estimées, aboutit à un nombre de Rayleigh de l'ordre de 106 à 108, ce qui est de toute façon très supérieur à la valeur critique : le manteau terrestre a donc un comportement globalement convectif.
Avec l'aide de Stéphane Labrosse (Laboratoire de géologie de Lyon, ENS de Lyon) et les relectures, sur le fond et la forme, de Cyril Langlois (prépa. agrégation ENS de Lyon) et Delphine Chareyron (Culture Sciences – Physique).