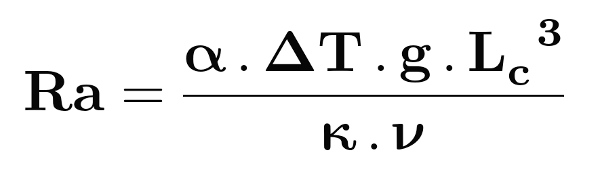Dynamique du manteau terrestre : mouvements et moteurs

Après relecture des articles ci-dessus, répondez aux questions suivantes.

1. Pourquoi les points situés à 670 et 5150 km de profondeur sont-ils des points d'ancrage pression-température (détection, interprétation, détermination de la température) ? Pourquoi la limite à 2900 km n'est-elle pas un autre point d'ancrage utilisé pour décrire le géotherme ?
2. D'après vos connaissances et d'éventuelles ressources complémentaires, comment le gradient thermique est-il déterminé dans la croute continentale, et dans la lithosphère ?
3. Comparez les gradients thermiques déterminés dans la lithosphère et dans le manteau sous-jacent. Que révèle l'existence même d'un gradient thermique à l'intérieur de la Terre ?
4. [Question subsidiaire] Après avoir rappelé ce qu'est un péridot, commentez l'affirmation suivante : « la péridotite représente bien la Terre silicatée ».

1. La limite à 670 km est bien connue sismiquement car il y a un saut de vitesse et la tomographie sismique montre c'est une limite physiquement importante puisque la lithosphère en subduction y reste parfois bloquée. Les expériences menées sur des péridotites à HP-HT montre que l'olivine passe par ses formes de haute pression (wadsleyite puis ringwoodite), transformations sismiquement “visibles”, avant une transformation majeure pour des pressions correspondant à la limite des 670 km : la dissociation de l'“olivine” en “bridgmanite + ferropériclase” (on trouve aussi les appellations “anciennes” de “(Si-)pérovskite + magnésiowustite”). Il est donc possible de reproduire en laboratoire cette transformation majeure en déterminant précisément ses conditions de pression et température (et donc la température si on connaît la profondeur qui est “traduite” en pression).

   À 5150 km, il s'agit de la transition entre le noyau externe liquide (ondes S non transmises) et le noyau interne solide (la graine). Là encore, il est possible de déterminer les conditions P-T de cette transition de phase expérimentalement et/ou par calcul. Contrairement au manteau supérieur dont ont possède des échantillons, la composition exacte du noyau est “calculée“ et ajustée pour répondre aux différentes contraintes connues (composition moyenne de la Terre, densité du noyau, transition liquide-solide, vitesses sismiques…). Malgré cela, les conditions P-T sont relativement bien contraintes à 5150 km.

   Par contre, à 2900 km, il s'agit de la limite entre deux milieux de chimies différentes : le manteau inférieur solide et le noyau externe liquide. Les seules contraintes sont que le manteau est solide (ce qui donne une large gamme de T possible à cette profondeur, jusqu'à la température de fusion du manteau à cette profondeur) et que le noyau est liquide (ce qui donne aussi une large gamme de T possible jusqu'à la température de cristallisation du noyau à cette profondeur). Le saut de température estimé à cette limite découle d'extrapolations de la température à partir des points à 670 et 5150 km et de gradients thermiques compatibles avec ce que l'on connait des propriétés des matériaux, de la convection et des données sismiques.

2. Par la mesure de la température dans les mines souterraines (croute continentale) et dans les puits de forages (croutes continentale et océanique), on obtient une mesure du gradient thermique dans la croute superficielle (10 à 80 K/km).

   La base de la lithosphère étant une limite physique du manteau (saut de vitesse, saut de viscosité, avec début de fusion partielle), on détermine les conditions P-T de cette transition qui est classiquement mise en relation avec l'isotherme 1300°C. Connaissant localement l'épaisseur de la lithosphère (5 à 150 km), on en déduit le gradient thermique moyen local et, si on a mesuré le gradient crustal local, on en déduira le gradient thermique local pour le manteau lithosphérique.

   On peut aussi déduire le gradient thermique superficiel de la mesure du flux géothermique et de la conductivité du matériau de surface [loi de Fourier, flux = conductivité × gradient thermique].

3. Le gradient thermique dans la lithosphère (généralement de 10 à 30 K/km) est bien supérieur à celui observé dans le manteau asthénosphérique (moins de 1 K/km, points d'ancrage à la base de la lithosphère, puis aux transformations successives de l'olivine, puis variations des vitesses sismiques mises en relations avec les densités et donc la T en fonction de la profondeur).

   L'existence de gradients thermiques avec les basses températures vers l'extérieur, montre que de la chaleur est évacuée/dissipée de l'intérieur de la Terre vers sa surface (puis l'atmosphère et l'espace). Des phénomènes de transfert de chaleur affectent donc la Terre, de son noyau à sa surface. Sans information, à ce stade, sur l'origine et/ou la production actuelle de chaleur.

4. Un péridot est une olivine (α) utilisable en joaillerie. En considérant que le terme s'applique à toutes les olivines des péridotites, mais aussi aux formes de hautes pressions (wadsleyite –olivine β– et ringwoodite –olivine γ), les péridots sont présents dans tout le manteau supérieur (28 % du volume de la Terre), or la Terre silicatée (croutes extraites du manteau supérieur, manteau supérieur, manteau inférieur) représente 84 % du volume terrestre (1+28+55).

   La péridotite, terme pris au sens de “roche silicatée qui contient effectivement des péridots au sens large”, ne représente donc que 33,3 % de la Terre silicatée (28/84).

   Le manteau inférieur ne comporte certes pas d'olivine mais a tout de même quasiment la même composition que le manteau supérieur (pour les éléments majeurs), on peut donc dire que la Terre silicatée à quasiment une composition chimique de péridotite (mais pas la minéralogie d'une péridotite).

Après relecture des articles ci-dessus, répondez aux questions suivantes.

1. Comment un modèle comme PREM est-il construit ? Comment le manteau terrestre est-il structuré dans un modèle sismique de ce type ?
2. Quel est le principe de la tomographie sismique ? Comment les “anomalies” mesurées sont-elles explicables / expliquées ?
3. Donnez un argument majeur en faveur de l'interprétation des anomalies positives comme étant la trace de la plongée de lithosphère dense, c'est-à-dire comme un mouvement de matière et non pas la présence d'une source immobile de matériau dense et/ou froid (voir, par exemple, la figure 1 de Déformations profondes de la lithosphère océanique subduite). [Subsidiaire] De quelle autre ”observation sismique” plus directe cette interprétation peut-elle être rapprochée ?
4. Expliquez l'intérêt des représentations en cartes des anomalies sismiques (anomalies à une profondeur donnée ou topographie d'une discontinuité sismique) comme celles des figures 7 de La Terre est “ronde”, 3 de Déformations profondes de la lithosphère océanique subduite, ou 1 et 2 de La zone de transition et la dynamique du manteau terrestre.

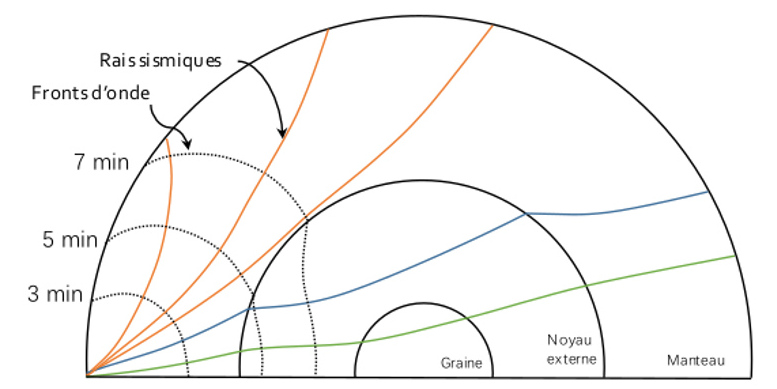
1. L'étude des sismogrammes permet d'étudier le temps d'arrivée des ondes sismiques en fonction de la distance épicentrale (distance entre l'épicentre du séisme et la station sismique), c'est l'étude des hodochrones. Sur ces courbes, on observe (1) des portions régulières (légèrement incurvées vers le bas du fait d'une accélération avec la profondeur), et (2) des sauts de temps montrant un brusque ralentissement ou une brusque accélération, qui correspondent alors à (1) la traversée de milieux homogènes à vitesse “constante”, ou plutôt à vitesse croissant régulièrement avec la profondeur, avec (2) le passage à certaines profondeurs d'interfaces physiques séparant des milieux marqués par un saut de vitesse de propagation des ondes sismiques, saut de vitesse lié, par exemple, à un saut de viscosité / ductilité, à une variation de densité lié à des réarrangements minéralogiques (compaction)…

   L'étude des données moyennes de vitesse et de profondeur des interfaces aboutit à la représentation de ces données sous la forme d'un modèle de Terre à enveloppes sphériques concentriques, par exemple le modèle PREM. Connaissant la vitesse à chaque profondeur et en partant d'une chimie péridotitique pour le manteau, on en déduit aussi un profil de densité avec la profondeur. Le manteau, lorsqu'il n'affleure pas, débute sous le Moho (interface croute / manteau). Du manteau au sommet de la LVZ/ZMV (low velocity zone / zone à moindre vitesse) on a le manteau lithosphérique “fragile” (par opposition à ductile), puis on a le manteau supérieur non lithosphérique ou asthénosphère, jusqu'à environ 670 km de profondeur. Des discontinuités sont perceptibles dans l'asthénosphère, vers 410 et 520 km. Puis, à partir de 670 km de profondeur, on a le manteau inférieur jusqu'à la discontinuité majeure de Gutenberg vers 2900 km de profondeur (limite manteau/noyau).

2. Après avoir construit un modèle à partir de l'étude de l'ensemble des données sismiques, on reprend chaque donnée pour la confronter au modèle. En effet, connaissant l'épicentre et la station sismique, on en déduit, d'après le modèle choisi, un trajet et un temps d'arrivée. On compare ce temps théorique au temps réel. On remarque alors parfois de légers décalages indiquant que l'onde s'est propagée plus vite ou moins vite que prévu : on sait alors que, sur ce trajet, une portion montre une anomalie de vitesse positive (onde plus rapide qu'en théorie) ou négative, sans savoir exactement où. En recoupant de multiples analyses, on va pouvoir localiser les points pour lesquels il y a systématiquement une accélération ou un ralentissement, et quantifier cette anomalie (de l'ordre du pourcent). Classiquement, on représente en teintes de bleu les anomalies latérales positives, et en teintes de rouge les anomalies latérales négatives. Attention, anomalie latérale signifie que deux points de même couleur à une même profondeur ont une même anomalie par rapport à la valeur théorique à cette profondeur et ont donc la même vitesse de propagation. Par contre, deux points de même couleur situés à deux profondeurs différentes ont la même anomalie relative (1 % par exemple), chacun par rapport à la valeur théorique correspondant à sa profondeur, ils n'ont donc pas la même vitesse de propagation des ondes sismiques.

   Les causes possibles d'anomalies de vitesse sont multiples et complémentaires. Si les ondes vont plus vite en un point, ce peut être dû à une composition chimique différente (et donc minéralogie plus ou moins différente dans le détail, voire degré de fusion partielle différent), à une densité plus forte, ou à une température plus faible. Sachant que la densité, à pression/profondeur donnée, augmente lorsque la température diminue, toute variation de densité/température, à chimie constante, correspond aussi à une variation de température/densité. Généralement on interprète rapidement les anomalies en terme de température, ce qui n'est pas faux mais n'est pas exclusif d'autres facteurs comme dans le cas de la subduction d'une lithosphère (croute + manteau partiellement hydratés et “froids”) dans du manteau asthénosphérique (manteau seul, ”non-hydraté” et à la température correspondant à sa profondeur).

3. En l'absence de signe de variation de la surface de la Terre (ni gonflement, ni rétractation), l'accrétion océanique à l'aplomb des dorsales doit être corrélée à la disparition de fonds océaniques en d'autres lieux : sans préjuger si l'accrétion entraine la disparition, ou la disparition entraine l'accrétion, ou si les deux phénomènes sont indépendants. Les coupes de tomographie sismique montrent que des anomalies positives présentes dans le manteau asthénosphérique forment des “cordons” qui s'ancrent en surface aux fosses océaniques des zones en convergence. Il est donc possible d'y voir la trace de la plongée de la lithosphère océanique hydratée et froide dans le manteau sous-jacent moins dense. Dans ce cas, la tomographie est un moyen de suivre le devenir de la lithosphère subduite tant que ces caractéristiques physico-chimiques la distinguent sismiquement de son environnement.

   Cette lithosphère subduite froide reste un temps “fragile” et donc sismiquement active dans son environnement asthénosphérique ductile. La superposition du plan de Wadati-Benioff (localisation de foyers sismiques dans un manteau à priori ductile) à ces anomalies positives au niveau des zones de subduction plaide donc en faveur de l'interprétation des anomalies de vitesse et des alignements sismiques comme des traces de plaques en subduction.

4. Si les coupes sismiques permettent par exemple de suivre la géométrie d'une anomalie avec la profondeur, les cartes à différentes profondeurs (des “écorchés” sismiques de la Terre) permettent de repérer l'étendue latérale des anomalies. Une telle carte à la profondeur d'une limite sismique importante permet de voir l'“épaisseur” de cette limite et son franchissement éventuel localement. S'il n'y a que de très faibles anomalies réparties aléatoirement, cela indique une limite quasi-“plane”, si les anomalies dessine des “vagues” cela indique des ondulations de cette limite, si des anomalies localisées sont présentes, cela marque alors la présence du franchissement local de la limite, la géométrie verticale de cette anomalie pourra alors être précisée par l'obtention de coupes adéquates.

   Surtout, ces cartes permettent de relier éventuellement des anomalies en profondeur aux structures de surface, continents mais surtout limites de plaques, dorsales et zones de subduction, grâce à la projection des limites et contours de surface sur les cartes analysées. Ainsi on voit que des anomalies des ondes de cisaillement (ondes S sensibles à la fusion partielle) sont présentes à 100 km de profondeur sous l'ensemble des dorsales océaniques, ce qui correspond bien à la profondeur d'une lithosphère “classique” et à la profondeur de fusion partielle débutante qui peut alimenter les dorsales. On voit d'ailleurs que cette anomalie chaude est bien plus large sous les dorsales les plus rapides. De telles cartes montrent très bien aussi que ces anomalies “chaudes” ne se prolongent pas en profondeur sous les dorsales quand on regarde les cartes à 410, 660 ou 2850 km : la fusion partielle alimentant les dorsales est donc un phénomène très superficiel qui n'est à relier à aucune remontée de matériel chaud profond ! Ces cartes permettraient aussi de déceler d'éventuels prolongements traversant la limite manteau supérieur / manteau inférieur.

Après lecture de la présentation de la formule et des paramètres du nombre de Rayleigh (et sans lire la suite dans un premier temps), répondez aux questions suivantes.

1. Que signifie le fait que la valeur critique au-delà de laquelle un système convecte a été déterminée de manière empirique ?
2. Expliquez “avec les mains”, sans équations, de manière qualitative, l'effet de la variation des différents paramètres (au moins 3 paramètres parmi α, g, κ, ν) sur la facilitation ou la limitation de la convection / de la conduction. Pour cela, on se pose la question de l'effet du paramètre sur l'efficacité à dissiper une petite anomalie thermique (penser aux forces en jeu – poids, poussée d'Archimède, résistance – et à la persistance de l'anomalie thermique).
3. Quels types d'études ont-ils permis la détermination de paramètres nécessaires au calcul du nombre de Rayleigh pour le manteau terrestre ?

1. La valeur critique permettant de considérer que le milieu est convectif est une valeur empirique, ce qui signifie qu'elle a été déterminée par l'étude de différents systèmes conductifs, convectifs et/ou de systèmes contrôlés dont on fait varier certains paramètres pour repérer les valeurs pour lesquelles ils passent d'un mode de transfert thermique à un autre. Cette valeur critique n'est pas le fruit de calculs théoriques de dynamique des fluides, elle ne découle pas de l'application d'une loi physique, mais est bien le résultat d'observations et de mesures expérimentales.

2. Prenons l'exemple d'une anomalie thermique locale affectant un volume initial V de masse M.

   Plus le paramètre $\alpha$ est élevé, plus l'anomalie thermique subit une variation de volume importante pour un écart de température donné. La masse de l'anomalie thermique est inchangée et donc son poids ne varie pas. Mais la poussée d'Archimède, égale au “poids de liquide déplacé”, est fonction du volume : “volume × masse volumique du milieu non perturbé × $g$”. Plus $\alpha$ est grand, plus la variation de volume engendrée est importante, plus l'effet sur la poussée d'Archimède est important. En cas d'anomalie “chaude”, la dilatation importante entraine une augmentation de la poussée d'Archimède à poids égal et favorise donc un mouvement de convection ascendant. À l'inverse, en cas d'anomalie froide, la contraction réduit fortement la poussée d'Archimède et favorise donc un mouvement de convection descendant, le poids étant,lui, inchangé. Ainsi, une augmentation du coefficient de dilatation thermique volumique $\alpha$ favorise les mouvements de matière, c'est-à-dire la convection.

   Le paramètre $g$ intervient dans l'expression des forces tendant à mettre en mouvement la matière : poids et poussée d'Archimède. Plus $g$ est élevé, plus ces forces sont importantes et donc, surtout, plus la force résultante tendant à faire remonter ou plonger la matière est importante. Il en découle qu'une augmentation de l'accélération de la pesanteur $g$ favorise, elle aussi, les mouvements de matière, c'est-à-dire la convection.

   Lorsque le paramètre $\kappa$ augmente, cela signifie que le milieu transfère plus facilement, plus rapidement la chaleur par conduction, ce qui a pour conséquence de dissiper plus rapidement toute anomalie locale de température par simple conduction. Les anomalies thermiques sont alors moins longuement intenses, les mouvements de matière ont donc moins de temps pour se mettre en place avant dissipation de l'anomalie par conduction. Autrement dit, une augmentation de la diffusivité thermique $\kappa$ favorise la conduction.

   Lorsque le paramètre $\nu$ augmente, le milieu résiste plus au mouvement, au fluage. Les mouvements de matière étant freinés, la dissipation des anomalies thermiques par conduction est alors favorisée. Une augmentation de la viscosité cinématique $\nu$ favorise donc la conduction.

   L'écart de température $\mathrm{\Delta T}$ intervient de concert avec la dilatation thermique volumique, c'est le produit $\alpha .\mathrm{\Delta T}$ qui représente la variation relative de volume. Lorsque $\mathrm{\Delta T}$ augmente, la variation de volume de l'anomalie thermique augmente et, donc, comme pour $\alpha$, une augmentation de la différence de température $\mathrm{\Delta T}$ favorise les mouvements de matière, c'est-à-dire la convection.

   Le paramètre $L_c$ est le plus difficile à aborder “avec les mains”. On peut passer cet écueil en invoquant l'usage d'un nombre sans dimension, Ra, et donc la nécessité de faire intervenir une longueur à la puissance 3 pour que le nombre de Rayleigh soit sans dimension, la seule “longueur” définissant le système étant l'épaisseur du système convectif $L_c$. Une autre manière est de présenter le nombre de Rayleigh comme le rapport, toujours sans dimension, des temps caractéristiques de mise en place des phénomènes de dissipation des anomalies thermiques que nous noterons ${\tau }_{\mathrm{diff.th.}}$ temps de diffusion thermique, ${\tau }_{\mathrm{rés.écoul.}}$ temps de résistance à l'écoulement, et ${\tau }_{\mathrm{conv.}}$ temps de mise en place de la convection. Ces phénomènes affectant l'ensemble du système, $L_c$ est prise comme dimension représentative de ce système. En ce qui concerne $\kappa$ et $\nu$, ces paramètres expriment des diffusivités, respectivement thermique et de quantité de mouvement, concernant une “surface” par “unité de temps”, en rapportant cela à la “surface caractéristique” par ”temps caractéristique” on écrit alors : $\kappa ={L_c}^2/{\tau }_{\mathrm{diff.th.}}$ et $\nu ={L_c}^2/{\tau }_{\mathrm{rés.écoul.}}$. Les “forces de convection”, $\alpha .\mathrm{\Delta T}.g$, ont la dimension d'une accélération, soit une longueur par unité de temps au carré, soit, une “longueur caractéristique” par “temps caractéristique de convection au carré”, d'où l'expression $\alpha .\mathrm{\Delta T}.g=L_c/{{\tau }_{\mathrm{conv.}}}^2$. Ainsi, lorsqu'on compare les temps caractéristiques de mise en place des phénomènes favorisant la conduction, ${\tau }_{\mathrm{diff.th.}}$ et ${\tau }_{\mathrm{rés.écoul.}}$ au temps caractéristique de mise en place de la conduction, ${\tau }_{\mathrm{conv.}}$, en gardant un nombre sans dimension, on écrit $\mathrm{Ra}=\frac{{\tau }_{\mathrm{diff.th}}.{\tau }_{\mathrm{rés.écoul.}}}{{{\tau }_{\mathrm{conv.}}}^2}$. La convection se met en place si le “temps” de résistance à la convection est bien plus grand que le “temps” de mise en place de la convection, c'est-à-dire si $\mathrm{Ra}>>1$. En utilisant les égalités précédentes faisant intervenir $L_c$ dans l'expression des temps caractéristiques, on se rend compte que la longueur caractéristique augmente toujours les temps caractéristiques mais pas avec la même “efficacité” et que le rapport des temps caractéristiques fait apparaitre $L_c$ au numérateur (et au cube), ce qui montre que la convection est au final favorisée par rapport à la conduction lorsque cette longueur augmente.

3. À partir d'échantillons de péridotite, on peut mesurer le coefficient de dilatation thermique volumique $\alpha$ et la diffusivité thermique $\kappa$ de ce matériau dans une large gamme de pression et de température.

   Les études sismiques et minéralogiques (transitions de phases) permettent la construction d'un modèle de Terre pour lequel on connait alors l'épaisseur des couches (donc $L_c$), la répartition des masses (donc $g$ à la surface mais aussi en tout point de l'intérieur de la Terre), et le géotherme moyen (donc un ordre de grandeur de $\mathrm{\Delta T}$).

   La viscosité du manteau est plus difficile à déterminer sur de petits échantillons à placer dans des conditions proches de celles du manteau. Une approche de la viscosité moyenne du manteau, au moins supérieur, est obtenue grâce à la détermination de vitesse de rééquilibrage isostatique suite à la fonte des glaciers d'Europe du Nord depuis 20 000 ans, voir, par exemple, à ce propos Les plages soulevées de Scandinavie et du Canada, conséquences du rebond post-glaciaire.

   La prise en compte des différents paramètres et de leur gamme de valeurs mesurées/estimées, aboutit à un nombre de Rayleigh de l'ordre de 10⁶ à 10⁸, ce qui est de toute façon très supérieur à la valeur critique : le manteau terrestre a donc un comportement globalement convectif.

Après (re)lecture des articles ci-dessus.

1. Quel est le principe de l'ombroscopie ? À quelle technique de mesure géologique indirecte peut-on rapprocher l'ombroscopie ?
2. Quel est l'intérêt de cette manipulation par rapport à celles utilisant des colorants ?
3. Quelles sont les limites de ce modèle si l'on s'intéresse au cas concret du manteau terrestre ?
4. [Question subsidiaire] Quel extrait vidéo vous parait-il utilisable pour illustrer la notion de “découplage mécanique” ?

1. L'ombroscopie permet de révéler des hétérogénéités d'indice de réfraction dans un milieu transparent (ici, un aquarium avec de l'eau ou de l'huile). Pour cela on éclaire l'aquarium perpendiculairement à sa longueur avec un éclairage unidirectionnel (rayons lumineux tous parallèles entre eux). En l'absence d'hétérogénéité d'indice de réfraction au sein des liquides, les rayons lumineux traversent de l'air, du verre, de l'eau (ou de l'huile), du verre, puis de l'air, avant d'éclairer l'écran. Ces changements de milieux se font selon des interfaces perpendiculaires au rayonnement (les parois de l'aquarium) ce qui n'engendre donc pas de réfraction [n₁.sin(i₁) = n₂.sin(i₂) est respecté pour i₁=i₂=90° car sin(90°)=0]. Lorsque des mouvements de convection prennent place, de l'eau chaude monte dans de l'eau plus froide et de l'eau froide descend dans de l'eau plus chaude. L'indice de réfraction de l'eau (de huile) étant fonction de la température (indice décroissant quand la température augmente), le liquide en convection présente donc des interfaces entre des formes ascendantes ou descendantes en 3D d'un certain indice et un milieu environnant d'un autre indice. Pour toute interface non perpendiculaire au rayonnement incident, il y a réfraction. Le point d'arrivée initial d'un rayon incident se verra donc décalé latéralement sur l'écran suite à cette réfraction (et même aux réfractions multiples lors de sa traversée de l'aquarium). Par rapport à l'image homogène de l'aquarium sans convection, les structures convectives traversées induisent une diminution de la luminosité là où les rayons ont été décalés et une augmentation de luminosité là où les rayons réfractés arrivent sur l'écran, en plus des rayons incidents non réfractés. On observe donc des zones d'ombre et des zones plus lumineuses sur l'écran) qui révèlent la présence d'hétérogénéités de réfraction liées à des hétérogénéités de température au sein du milieu traversé. Les mouvements (et les hétérogénéités) se déplaçant ”vite” on peut suivre le déplacement des masses d'eau chaudes ou froides.

   Cette technique permet donc de mettre en évidence la présence de milieu d'indices de réfraction ”différents” sur le trajet d'un rayon lumineux. Cela rappelle la tomographie sismique qui étudie la présence de milieu plus “rapide” ou plus “lent” sur le trajet d'un rai sismique.

2. Avec l'emploi de colorants on peut penser modifier légèrement les propriétés physiques (densité, viscosité) du milieu coloré par rapport au milieu “brut”, et donc observer des mouvements qui ne seraient pas dus qu'à la différence de densité de l'eau. Mais surtout, avec les colorants on ajoute l'observation du phénomène de diffusion des colorants qui s'ajoute à la convection. On observe donc des mouvements d'eau colorée même dans un éventuel montage témoin sans convection (ni chauffage, ni refroidissement, tout à température ambiante). De plus, au bout de quelques minutes l'ensemble de l'eau est colorée de manière plus ou moins uniforme et il devient difficile d'observer quoi que ce soit. Autre inconvénient, si on veut refaire l'expérience, il faut vider l'eau, re-remplir l'aquarium, attendre la stabilisation de l'eau, puis réintroduire les colorants. Avec l'ombroscopie, pas de mouvement observé sans convection, observation possible sur une plus longue durée (pas de couleur homogène), remise à l'état initial en arrêtant chauffage et refroidissement (il faut parfois attendre un peu l'homogénéisation thermique, mais aucune manipulation particulière à faire).

   Si la réalisation en classe semble plus difficile car la présence d'un groupe d'élèves peu perturber l'expérience (passages entre la “lampe” et l'aquarium et entre l'aquarium et l'écran), il faut penser à la possibilité de filmer l'expérience pour la rediffuser en direct sur des écrans d'ordinateur ou sur un autre écran. Comme pour l'expérience avec les colorants, il semble important de présenter au moins une observation en direct, même si on peut ensuite compléter ces observations par des enregistrements d'autres séances.

3. Ce modèle à deux couches a de nombreuses différences avec le manteau terrestre, si on voulait y voir une tentative de modélisation de la convection dans le manteau inférieur (ici, l'eau) et le manteau supérieur (ici, l'huile). Le manteau est solide avec des mouvements lents alors qu'ici les milieux observés sont liquides et animés de mouvements rapides. Manteau inférieur et manteau supérieur sont de composition chimique identique alors que le modèle prend deux composés chimiques très différents et immiscibles rendant impossibles les passages de matière d'une couche à l'autre (ni panaches ni “plaques” ascendants ou descendants ne peuvent traverser l'interface dans ce modèle). Bien sûr, les variations de pression au sein des couches du modèle ne permettent pas de reproduire les variations de densité, les changements de phase, la fusion partielle… observés dans le manteau. Le saut de viscosité entre l'eau et l'huile est de l'ordre de 100 alors qu'il est plutôt de l'ordre de 10 à l'interface manteau inférieur / manteau supérieur, mais surtout il est dans l'autre sens : le manteau inférieur est plus visqueux, alors qu'ici c'est l'huile “supérieure” la plus visqueuse. Dans ce modèle, le chauffage vient uniquement de la base, pas de la masse… Et bien d'autres “manques”…

   Mais alors à quoi peut servir ce modèle ?

   Ce modèle permet d'observer des mouvements de convection, avec des panaches ascendants (bien visibles dans le dernier film réalisé pour cela) ou descendants (bien visibles dans le film à une seule couche avec initiation de panaches descendants au contact du bac de glaçons). Il permet aussi d'observer un transfert vertical de chaleur à travers deux niveaux convectifs et une interface conductrice (pas d'échange de matière, donc le transfert de chaleur se fait par conduction). On peut observer un découplage mécanique (pas d'effet d'entrainement) possible entre deux niveaux convectifs à une interface avec un saut de viscosité. On peut aussi avec ce modèle aborder un peu de physique optique en expliquant l'ombroscopie et/ou la notion d'observation indirecte.

4. L'observation d'un découplage mécanique (pas d'effet d'entrainement à une interface physique) est visible dans les films à deux couches lorsqu'on voit un mouvement vers la droite du sommet de la couche d'eau et vers la gauche de la base de la couche d'huile. Dans la seconde partie du deuxième film à deux couches, lorsque le bac à glaçons est placé au centre de l'aquarium, on peut voir que le sommet de la couche d'eau va toujours vers la droite et que, dans l'huile, le mouvement basal est vers la gauche à gauche du bac froid et vers la droite à droite de ce bac. On pourrait alors pousser l'expérience pour voir s'il est possible de déceler une différence de vitesse selon que les mouvements sont de même sens ou de sens opposés, c'est-à-dire de voir s'il existe tout de même une force de frottement à l'interface dont l'effet serait observable. Quoi qu'il en soit, cette observation permet d'illustrer le concept de découplage mécanique, découplage dont il est possible de parler, par exemple, à l'interface manteau inférieur / manteau supérieur ou à l'interface asthénosphère / lithosphère (les déplacements des plaques lithosphériques n'étant pas (ou très partiellement) dus à un entrainement par les mouvements de convection dans l'asthénophère sous-jacente).

   On observe aussi un découplage au début du premier film à deux couches lorsque l'huile n'est pas refroidie par le bac à glaçons. En effet, on voit bien le mouvement vers la droite du sommet de la couche d'eau, et on observe que ce mouvement n'entraine pas du tout la base de la couche d'huile dans laquelle la convection ne forme pas des “cellules” mais plutôt des “piliers”.

Après avoir revu les étapes précédentes et après (re)lecture des articles ci-dessus.

1. Décrivez brièvement les caractéristiques des couches limites thermiques du système mantellique convectif (couches au niveau desquelles le transfert de chaleur se fait par conduction, couches faisant partie du système mantellique convectif et séparant du manteau convectif d'un autre système, convectif ou non).
2. D'après les images de tomographie sismique, expliquer ce qui semble indiquer que la subduction est plus importante pour les déplacements horizontaux des plaques lithosphériques que l'accrétion aux dorsales océaniques (on pourra, par exemple, rappeler l'origine des forces exercées par la subduction et les dorsales, et/ou expliquer en quoi les “images” sismiques seraient différentes si l'accrétion était un moteur plus important que la subduction).
3. Sur quelles observations / données se base-t-on pour établir un modèle géologique de mouvement des plaques de type NUVEL ? Quel outil supplémentaire utilise un modèle dit géodésique de type MORVEL, et quelles différences peut-on attendre ?
4. [Question subsidiaire] Quelle type de vitesse doit-on utiliser si on veut tester l'importance de la subduction ou de l'accrétion sur les déplacements horizontaux des plaques ? Qu'apporterait la mise en évidence d'une relation entre « vitesse d'accrétion et pourcentage* de subduction aux frontières de plaques » (* comprendre pourcentage de frontière d'une plaque qui est en subduction) ?

1. La couche limite thermique supérieure “froide” du manteau est la lithosphère conductive, qui sépare le manteau convectif de l'atmosphère convective “froide”. Cette couche limite est constituée de manteau “froid” surmonté de croute océanique ou continentale. De la lithosphère océanique âgée et dense retourne dans le système convectif dans les zones de subduction.

   La couche limite thermique inférieure “chaude” du manteau est la couche D", qui sépare le manteau convectif du noyau externe “chaud” lui aussi convectif. Cette couche complexe a une chimie mantellique un peu particulière du fait d'échanges chimiques possibles avec le noyau sous-jacent mais surtout parce que c'est là que finissent les lithosphères océaniques subduites (au moins certaines). De plus, les conditions de pression et de température sont telles qu'une phase de haute pression de la “perovskite” (bridgmanite), la “post-pérovskite” (post-bridgmanite ?), peut s'y développer, y revenir à sa forme bridgmanite par augmentation de température. Chimie et cristallographie induisent ici des conditions particulières de formation de magmas denses (cf. Crypto-continents et crypto-volcans à la frontière noyau-manteau).

   À la limite manteau inférieur / manteau supérieur, lorsque de la lithosphère subduite s'étale sur cette interface, on pourrait penser à une couche limite thermique entre deux portions convectives de manteau. Mais, si cette lithosphère est encore un peu plus froide que le manteau alentour, elle est “réchauffée” par le haut et par le bas et ne correspond pas à une couche conductive à replacer dans le cadre général de dissipation de chaleur de l'intérieur de la Terre vers sa surface. Dans l'ancien modèle à deux niveaux de convection mantellique, une couche limite thermique, même mince, devait correspondre à la limite manteau inférieur / supérieur. Cette limite, physique et non chimique, n'empêche pas des mouvements ascendants ou descendants de manteau au travers de cette “frontière” ; la matière change de formes cristallines dominantes au passage (en déformant la limite le temps que les transformations aboutissent).

2. La force de poussée des dorsales correspond à la poussée de la lithosphère qui “glisse” sur le sommet du manteau asthénosphérique, de l'axe surélevé de la dorsale vers la plaine abyssale. Cette poussée est d'autant plus importante que le dénivelé et la charge (poids de la lithosphère) sont importants.

   La force de traction de la lithosphère subduite est due à la force exercée par la lithosphère “coulant” dans le manteau sous-jacent, c'est la différence entre le poids de la lithosphère subduite et la poussée d'Archimède exercée sur cette dernière par le manteau asthénosphérique. Cette traction est donc d'autant plus importante que la différence de masse volumique est importante (différence qui croît avec la profondeur du fait de la déshydratation et de l'éclogitisation de la lithosphère océanique) et le volume de lithosphère subduite encore reliée mécaniquement à la lithosphère de surface, volume qui est d'autant plus important que la subduction va “loin” en profondeur.

   Les dorsales sont des reliefs qui impliquent seulement la partie superficielle du manteau asthénosphérique convectif, comme le montre la tomographie sismique. Les subductions, elles, descendent au moins jusqu'à 670 km de profondeur, passent par endroits dans le manteau inférieur et atteignent parfois la base du manteau. La lithosphère subduite doit cependant être en continuité mécanique avec la surface pour exercer une traction efficace, mais aussi être assez rigide car sinon un part importante de la “traction” est “absorbée” dans les déformations de la lithosphère devenant plus ductile. Une rigidité certaine étant attestée jusqu'à au moins 400 km de profondeur, on peut, en première approximation, estimer qu'une force de traction efficace est probablement exercée jusqu'à la limite manteau inférieur / manteau supérieur. On a donc, d'une part, une force de poussée liée à un phénomène relativement superficiel et, d'autre part, une force de traction liée à des mouvements à l'échelle au moins du manteau supérieur.

   Si le rôle de la poussée était prédominant, on pourrait s'attendre à des reliefs plus élevés aux dorsales, liés à une forte épaisseur de manteau convectif “chaud” à leur aplomb (et donc un fort relief par réajustement isostatique), alors que la lithosphère en subduction, poussée, plongerait plus “horizontalement” en sous-placage sous la lithosphère chevauchante. Le réchauffement de cette lithosphère sous-plaquée empêcherait / limiterait alors peut-être sa densification et sa déshydratation et, par conséquent, sa plongée dans le manteau sous-jacent.

3. Le modèle NUVEL (Northwestern University VELocity model) se base sur les anomalies magnétiques de part et d'autre des dorsales pour mesurer les vitesses relatives d'écartement des plaques (l'anomalie choisie donne des vitesses moyennes sur les 2 derniers millions d'années). Les azimuths des failles transformantes (mouvements en décrochement) permettent de donner la direction locale de mouvement relatif (l'azimuth d'un plan est la direction par rapport au Nord des lignes horizontales de ce plan). L'étude des mécanismes au foyer permettant, lui, de donner le sens de mouvement relatif des plaques. Les contours des plaques sont les dorsales, les grandes transformantes (San Andreas), et les limites en convergence, fosses de subduction et collision (zones sismiquement actives pour lesquelles des mouvements relatifs sont observables mais dont les vitesses ne sont pas ici mesurées). Les vitesses relatives des zones de subduction / collision sont estimées à partir des vitesses d'accrétion, en tenant compte du fait qu'à l'échelle globale il y a autant de “création” de surface que de “disparition”.

   Le modèle MORVEL (Mid-Ocean Ridge VELocity model) mesure aussi des vitesses d'accrétion par les anomalies magnétiques océaniques (avec une anomalie plus jeune pour les dorsales rapides) mais ce modèle ajoute l'utilisation des données GPS pour déterminer des vitesses (direction et intensité) dans les zones de convergence et pour mettre en évidence des mouvements intraplaques. Ceci permet donc de délimiter de nouvelles plaques que le modèle NUVEL ne peut prendre en compte car n'ayant pas de limite avec une dorsale assez développée et âgée. Ainsi, bien que connu, le rift Est-africain ne peut être pris comme limite de plaque dans le modèle NUVEL. Dans MORVEL, la plaque “africaine” donne trois plaques distinctes (Nubie à l'Ouest, Somalie au Nord-Est, et Lwandle au Sud-Est) car les mesures GPS permettent de quantifier les mouvements relatifs de part et d'autres des rifts sismiquement actifs mais non-océanisés. Le premier modèle MORVEL comprenait 25 plaques alors que NUVEL n'en a que 12. La prise en compte d'une trentaine de micro-plaques a ensuite donné un modèle à 56 plaques (les mouvements aux frontières des micro-plaques “absorbent” plus ou moins de déplacements, ce qui permet de préciser les mouvements aux frontières des plaques majeures).

   Le modèle NUVEL est limité en ce qui concerne le nombre de plaques prises en considération du fait de l'usage exclusif des rides océaniques pour la détermination des vitesses relatives de déplacement, et les vitesses “instantanées” mesurées sont des vitesses moyennes sur plus de 2 millions d'années (ce qui reste relativement “instantané” à l'échelle de l'âge de la Terre et même de la tectonique des plaques. Certaines limites géologiquement actives, tel le rift Est-africain, ne peuvent être définie par NUVEL comme des limites de plaques faute de détermination possible d'une vitesse d'accrétion.

   Le modèle MORVEL permet la prise en compte de toutes les limites actives connues grâce à l'usage des mesures GPS. Les vitesses dérivent de mesures sur des temps variables de 2 (comme NUVEL) à moins de 1 million d'années (pour les dorsales rapides) et des vitesses moyennes sur quelques années seulement. Les vitesses des zones de convergence ne sont plus déduites à partir des vitesses d'accrétion océaniques mais aussi à partir de mesures directes, ce qui permet de mieux répartir les “disparitions” compensant l'accrétion aux dorsales et les extensions de type rift.

   Dans les deux cas des calculs NNR, pour no net rotation, sont effectués, ils minimisent la somme de tous les vecteurs mouvement des plaques, ce qui minimise les mouvements par rapport aux forces d'inertie de la Terre, et permet d'obtenir des vitesses de type “absolues” sans avoir à fixer à priori des points immobiles (points chauds).

4. Pour comparer les vitesses des plaques, il faut utiliser des vitesses “absolues” (référentiel de points chauds ou no net rotation), et même exprimée en vitesses angulaires puisque les vitesses linéaires dépendent de la latitude eulérienne à laquelle on se place (vitesse nulle aux pôles et maximale à l'équateur), ou alors en vitesses linéaires équivalentes (même latitude eulérienne, vitesse “équatoriale” par exemple).

   Comparer « vitesse d'accrétion » et « pourcentage de subduction » revient à comparer deux valeurs ne décrivant pas le même objet. En effet, le pourcentage de limite de plaque en subduction décrit la plaque choisie. Par contre une vitesse d'accrétion est une vitesse qui concerne deux plaques, on ne peut l'attribuer entièrement à l'une ou l'autre plaque, et pour une plaque comme Nazca quelle vitesse doit-on prendre, celle de la dorsale la séparant de la plaque Pacifique ou celle de la dorsale la séparant de la plaque Antarctique ? Imaginons un instant (mais pas trop longtemps) que ce dernier problème soit soluble et qu'on trouve une corrélation positive entre vitesse d'accrétion et pourcentage de subduction, cela montrerait qu'il y a… corrélation. Mais cela n'indiquerait pas si c'est la vitesse d'accrétion (et la poussée) qui induit de la subduction, ou si c'est la présence de beaucoup de subduction (et de traction) qui induit une ouverture plus rapide des dorsales !

   C'est donc bien la vitesse absolue de déplacement des plaques que l'on peut comparer à leur « pourcentage de subduction » comme l'on fait dès 1975 Forsyth et Uyeda (ils ont aussi testé le pourcentage de dorsales) et mettre en évidence que les plaques les plus rapides sont celles qui présentent le plus fort pourcentage de limite de plaque en subduction. Ce fut la première approche pour apporter une réponse à la question de l'importance relative de la poussée des dorsales et de la traction des subductions dans les mouvements horizontaux des plaques.