Article | 29/01/2020
Interférométrie radar : principes et utilisation dans la surveillance de la déformation du sol
29/01/2020
Résumé
Principes de l'InSAR : acquisition des données, amplitude et phase, perturbation et interprétation du signal.
Table des matières
- Satellites SAR (Synthetic Aperture Radar)
- Images d'amplitude, images de phase
- Méthode InSAR et mesure de la déformation du sol
- Valeur des pixels dans un interférogramme
- Déroulement d'un interférogramme (unwrapping)
- Lecture d'un interférogramme
- Altérations du signal dans un but d'observation de la déformation
- Une fiche de synthèse
- Que fait-on des données d'interférométrie radar ?
- Bibliographie
L’imagerie satellitaire radar[1] est une technique d’imagerie qui utilise le domaine des micro-ondes (typiquement, longueur d'onde entre 1 et une vingtaine de centimètres). Par rapport à l’imagerie satellitaire optique, l’utilisation de ces longueurs d'ondes offre l’avantage d’être assez peu sensible aux nuages et permet de travailler à peu près quelles que soient les conditions météorologiques. Autre avantage, alors que l’imagerie satellitaire optique utilise la lumière du Soleil pour réaliser les images (méthode passive), l’imagerie radar est un système actif. En effet, la source d’énergie est embarquée dans le satellite, les ondes émises interagissent avec la surface du sol et reviennent vers le satellite. On peut ainsi réaliser des mesures à toute heure du jour et de la nuit.
Cet article présente les principes de l'interférométrie radar et son utilisation pour la surveillance de la déformation du sol. Les premières sections restent très qualitatives et peuvent être comprises par des étudiants en post-bac (BCPST ou ST) sans trop de problèmes. Les principales notions physiques sont vues en lycée, un élève de lycée (1re S ou spécialité physique) peut tout à fait comprendre cette méthode.
L'interférométrie radar peut être utilisée pour différentes mesures, telles que la mesure de la déformation du sol ou le calcul de modèles numériques de terrain. Ici, seule la mesure de la déformation sera abordée. Les principes d'obtention d'une image radar ainsi que les étapes calculatoires d'obtention d'un interférogramme donnant la mesure de la déformation ne seront pas abordés. L'objectif de cet article est de donner les principes de base permettant de lire et comprendre un interférogramme.
Dans cet article, les exemples géologiques concernent tous des déformations du Piton de la Fournaise (ile de La Réunion) lors de divers évènements dont l'éruption d'avril 2007 (cf. Effondrement du cratère Dolomieu, caldeira sommitale du Piton de la Fournaise (île de La Réunion) et Ile de La Réunion : l'éruption du Piton de la Fournaise, avril 2007).
L'InSAR et surtout son application à l'étude des failles et séismes ont été présentés dans la partie Imagerie radar et géodésie spatiale de la conférence Imagerie satellitaire et géodésie spatiale : de nouvelles données et techniques pour l'étude du cycle sismique des grandes failles actives.
Satellites SAR (Synthetic Aperture Radar)
Un satellite capable de faire de l'interférométrie radar est un satellite dit actif : il éclaire lui-même l'objet qu'il observe en émettant une onde radar (de longueur d'onde généralement comprise entre 1 et 20 cm), et en récupérant le signal renvoyé par la Terre. Il fonctionne de manière similaire à un appareil photographique équipé d'un flash. Les satellites radar ne sont pas équipés de lentilles comme les satellites optiques, mais d'une antenne, et sont capables de synthétiser une image à partir d'un signal enregistré en continu. Cette étape de synthèse sort du cadre de notre étude, mais c'est elle qui a donné son nom aux satellites : on parle de satellites SAR pour Synthetic Aperture Radar. On parle ainsi, pour l'interférométrie par satellite radar, de méthode InSAR (Interferometric Synthetic Aperture Radar).
Figure 1. Quelques-uns des satellites utilisés en InSAR
ENVISAT, lancé en 2002, est peut-être le plus célèbre mais n'est plus en activité depuis 2010. Le premier satellite Sentinel a été mis en orbite en 2014 et les satellites de cette série sont opérationnels en InSAR.
Source - © 2019 A. Augier / CC BY-SA 4.0
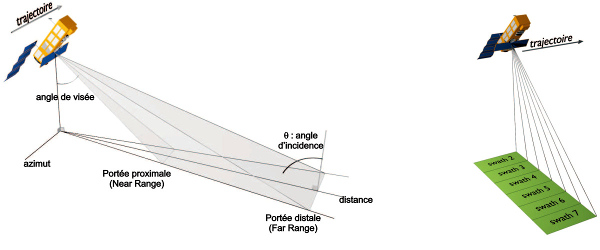
Figure 2. Quelques paramètres du faisceau radar
Par convention, les satellites SAR « visent toujours vers la droite » », perpendiculairement à leur trajectoire. Certains d'entre eux sont capables de viser avec un angle de visée ajustable. Ainsi, le radar ASAR du satellite ENVISAT peut viser selon 7 angles différents : chaque mode est appelé swath. (cc-by-sa Augier)
Images d'amplitude, images de phase
Comme la lumière, une onde radar est une onde électromagnétique, caractérisée par une longueur d'onde comprise généralement entre 1 et 20 cm. Le signal réémis par la Terre pour une zone donnée est donc caractérisé par son amplitude et sa phase, que le satellite est capable de mesurer.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 3. Image de phase et d'amplitude
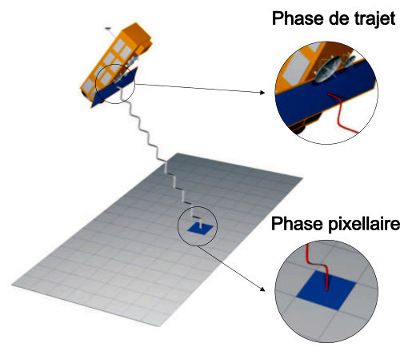
Une onde est caractérisée par une longueur d'onde (λ) et une amplitude. Les satellites SAR envoient une onde radar de longueur d'onde fixe. L'onde rétrodiffusée peut avoir une amplitude variable à cause des propriétés du sol, mais sa longueur d'onde reste identique. En revanche, les satellites SAR sont capables d'enregistrer la phase du signal rétrodiffusé, qui sera comprise entre 0 et 2π. Cette phase dépend de deux paramètres principaux : (1) la phase pixellaire, qui dépend des propriétés du sol, de la végétation et des “objets“ présents..., et qui peut être différente pour deux pixels contigus, (2) la phase de trajet, qui ne dépend que de la distance entre le sol et le satellite.
L'amplitude du signal reçu dépend des propriétés du sol (le signal est plus ou moins réfléchi, transmis ou diffusé) et correspond à la quantité de lumière revenant vers le satellite. Par exemple, une zone lisse aura tendance à réfléchir le signal comme un miroir et, vu l'obliquité du faisceau, ce signal ne revient pas au radar. La zone lisse apparaitra sombre sur l'image d'amplitude. À l'opposé, les surfaces rugueuses et les pentes dirigées vers le satellites apparaitront lumineuses.
La phase du signal reçu dépend de la phase pixellaire (due à la nature du sol et des objets qui y sont présents), et de la phase de trajet, qui ne dépend que de la distance entre le satellite et le sol. Formées de points dont la couleur (du blanc au noir – selon une nuance de gris – ou selon une échelle de couleur arbitraire) correspond à une valeur de phase comprise entre 0 et 2π, les images de phase ressemblent à du bruit, et ne sont pas exploitables en tant que telles.
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 4. Image d'amplitude et de phase (TerraSAR)
Exemples d'images de phase et d'amplitude au niveau du Piton de la Fournaise, prises par le satellite TerraSAR.
Méthode InSAR et mesure de la déformation du sol
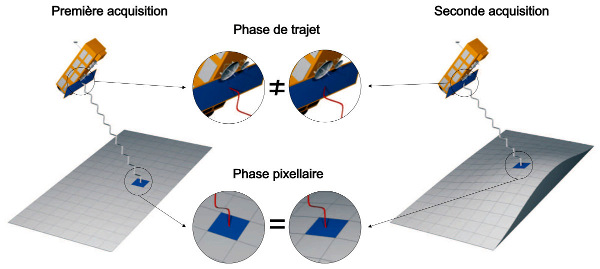
L'interférométrie SAR (InSAR) permet d'exploiter l'information de distance contenue dans l'image de phase. Une acquisition d'une image de phase est faite à deux dates différentes.
- Si la nature du sol reste constante, la phase pixellaire restera aussi constante et sera la même sur les deux images, toutes choses égales par ailleurs.
- Si le satellite occupe exactement la même position lors des deux acquisitions, et que le sol n'a pas bougé, alors la distance entre le satellite et chaque point de la Terre est exactement la même, la phase de trajet des deux images sera la même et les deux images de phase seront strictement identiques.
- En revanche, si le sol a bougé entre les deux acquisitions, les valeurs de phase de trajet pourront être différentes, et ne dépendront que de la quantité de déplacement.
En faisant la différence entre les deux valeurs de phase, on a donc accès à la quantité de déplacement d'un pixel dans la direction du satellite.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 5. Principes de l'InSAR
Principes de l'interférométrie radar : une image de phase est acquise à deux moments différents. Si la phase pixellaire est restée constante entre les deux images et que le satellite est dans la même position entre les deux prises de vue (ou qu'une correction de position est faite), la différence de phase de trajet entre les deux acquisitions ne dépendra que du déplacement du sol dans la direction du satellite.
Valeur des pixels dans un interférogramme
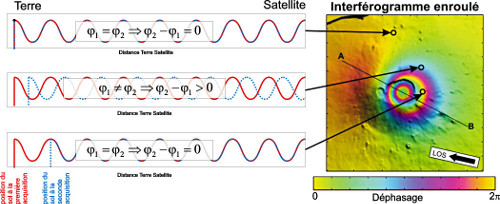
Un interférogramme correspond à la différence entre les deux images de phase, il est donc assimilable à une carte de déplacements du sol dans la direction du satellite.
- Si la différence de trajet aller-retour est inférieure à la longueur d'onde λ, la différence entre les deux valeurs de phase sera comprise entre 0 et 2π.
- Si la différence de trajet aller-retour est strictement égale à la longueur d'onde λ, alors la valeur de phase enregistrée sera la même pour les deux images, et leur différence sera égale à 0.
- Enfin, si la différence de trajet aller-retour est supérieure à la longueur d'onde λ, la seconde valeur de phase étant elle même comprise entre 0 et 2π, la différence des valeurs de phase sera encore comprise entre 0 et 2π comme dans le cas d'un déplacement inférieur à la longueur d'onde.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 6. Les franges dans un interférogramme
Le déphasage de 0 à 2π est cartographié à l'aide d'une échelle de couleur allant pour des valeurs croissantes du jaune au vert, au bleu clair, au bleu (opposition de phase), au violet, à l'orange puis au vert avant de revenir au jaune. Ceci dessine des bandes ou franges colorées. On appelle interfrange (et parfois abusivement “frange”) la distance entre deux bandes consécutives de même couleur correspondant à un déphasage allant de 0 à 2π (d'une bande jaune à la suivante).
Entre deux bandes consécutives de même couleur (donc de même phase), la différence de trajet aller-retour satellite-sol correspond à une différence égale à la longueur d'onde du signal et correspond donc à une différence de distance satellite-sol égale à une demi-longueur d'onde (1/2 aller + 1/2 retour = 1).
Explication des franges sur les interférogrammes : si le déplacement du sol dans l'axe de visée du satellite (désigné par LOS pour Line Of Sight, ligne de visée) correspond à 0 ou à un multiple de la demi-longueur d'onde de l'onde radar, alors la valeur de la différence des phases est égale à 0. Une frange peut donc être vue comme une ligne de niveau de déplacement.
Pour une brève présentation de l'interférométrie radar comme exemple de figure d'interférence, se reporter à la vidéo de La physique animée : une série de vidéos de physique - Superposition de phénomènes ondulatoires : les moirés (de 1min07s à 2min23s).
Déroulement d'un interférogramme (unwrapping)
Le déroulement permet, en comptant le nombre de franges, de convertir les déplacements en phase en déplacements en mètres dans la ligne de visée du satellite.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 7. Déroulement d'un interférogramme
Sur l'interférogramme, en partant d'un point de référence supposé immobile entre les deux prises de vues, on attribue à chaque bandes colorée la valeur de déphasage correspondante mais en ajoutant 2π lorsqu'on a parcouru une interfrange complète, ce déphasage cumulé est alors converti en déplacement cumulé (2π correspondant à une distance satellite-sol d'une demi longueur d'onde du signal radar).
Sur un interférogramme, une (inter)frange correspond à un déplacement cumulé du sol d'une longueur d'onde du signal radar utilisé. En comptant le nombre de franges et comme l'on connaît la longueur d'onde utilisée, on peut donc revenir aux déplacements en mètres dans la ligne de visée du satellite. Cette procédure s'appelle le déroulement.
Lecture d'un interférogramme
Quantité de déplacement
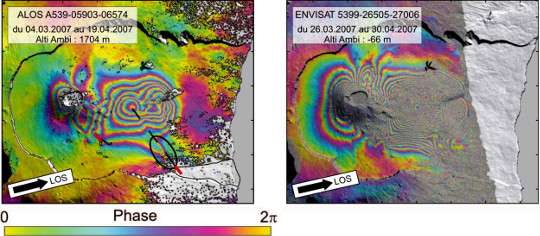
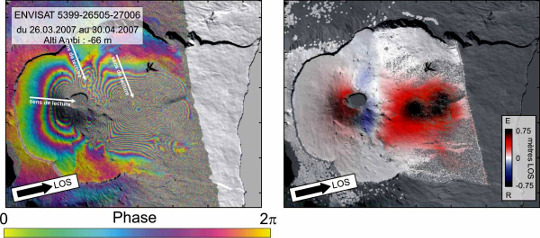
Une interfrange correspond à un déplacement cumulé d'une demi-longueur d'onde. Par exemple, ASAR (le radar d'ENVISAT) utilise une longueur d'onde de 5,66 cm alors que PALSAR (ALOS) utilise une longueur d'onde de 23,6 cm. La même déformation enregistrée par ces deux satellites ne donnera pas le même nombre de franges. En revanche, plus les franges sont nombreuses et serrées, et plus le déplacement est important. Le suivi du Piton de la Fournaise en avril 2007 (figure ci-dessous), par exemple, montre qu'avec PALSAR, dans le flanc Est, on compte 6 franges, ce qui correspond à 71 cm de déplacement.
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 8. Effet de la longueur d'onde du radar du satellite – Piton de la Fournaise, avril 2007
L'éruption d'avril 2007 vue par ALOS-PALSAR (à gauche) et ENVISAT-ASAR (à droite). Les lignes de visée (LOS) pour chaque image sont très similaires. La forme globale des motifs de déplacement est la même, en revanche le nombre de franges est environ 5 fois plus important à droite qu'à gauche : la longueur d'onde du radar PALSAR est en effet 5 fois plus grande que celle d'ASAR (23,6 et 5,6 cm, respectivement).
Direction des déplacements
N'oublions pas qu'un interférogramme correspond bien à une carte de déplacement dans l'axe de visée du satellite. Une même déformation visualisée dans deux lignes de visées différentes par le même satellite donnera donc deux interférogrammes pouvant avoir des aspects différents. Contrairement au GPS qui enregistre la déformation dans les 3 composantes géographiques (EW / NS / verticale), un interférogramme n'enregistre en fait que le projeté des déplacements dans l'axe de visée du satellite.
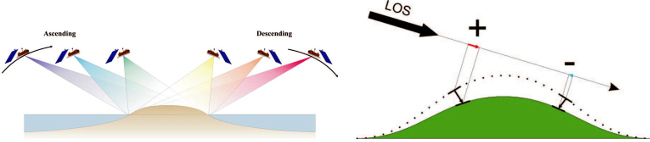
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 9. Effet de la ligne de visée, principes
À gauche, une même zone peut être vue selon différentes lignes de visée (ou LOS, line of sight), en fonction de l'orientation de l'antenne radar et du sens de passage du satellite (passe ascendante ou descendante).
À droite, deux pixels sur un terrain en subsidence (par exemple, un volcan qui se dégonfle) n'ont pas forcément la même direction de déplacement. Le satellite enregistre le projeté du vecteur de déformation sur l'axe de visée du satellite. En fonction de cette ligne de visée, un même déplacement ne sera pas enregistré de la même manière. Un déplacement perpendiculaire à l'axe de visée du satellite ne sera pas enregistrable.
Un même événement enregistré dans des lignes de visée différentes pourra donc amener à des interférogrammes d'aspects différents.
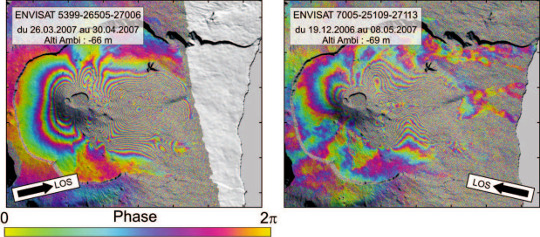
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 10. Effet de la ligne de visée sur des données réelles
Les déformations accompagnant l'éruption d'avril 2007 du Piton de la Fournaise vue dans deux lignes de visée différentes. À gauche, en passe descendante swath 6, et à droite, en passe ascendante swath 5. Les motifs de déformation, bien que localisés globalement aux mêmes endroits, ont des aspects différents. (cc-by-sa Augier/OPGC)
Sens des déplacements
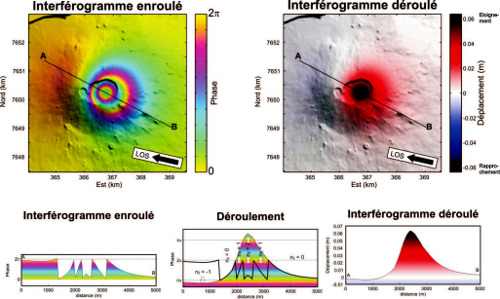
Pour déterminer le sens des déplacements, on part d'un endroit qui n'a pas bougé, puis on suit l'ordre des couleurs vers un endroit qui a beaucoup bougé (flèches blanches). Sur la figure ci-dessous, pour le motif le plus à l'Ouest, on part du vert, puis on passe au rose, puis au jaune, puis au vert, puis à nouveau au rose.... : la valeur de la phase augmente, la distance Terre-satellite a donc augmenté, et comme le satellite est fixe, c'est le sol qui s'est éloigné du satellite. C'est l'inverse pour les lobes d'orientation Nord/Sud à l'Est du cône central (flèche du milieu).
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 11. Interférogramme enroulé et déroulé
Le même interférogramme couvrant l'éruption d'avril 2007 enroulé et déroulé. Les lobes d'orientation Nord/Sud à l'Est du cône central correspondent à un rapprochement vers le satellite alors que les signaux à l'Ouest du cône et dans le flanc Est du volcan correspondent à un éloignement du sol par rapport au satellite. Dans ces différents motifs colorés, les franges ne “tournent” pas dans le même sens : jaune-rose-bleu pour le premier motif (les lobes à l'Est du cône central), jaune-bleu-rose pour le deuxième (flanc Ouest) et le troisième (flanc Est).
Altérations du signal dans un but d'observation de la déformation
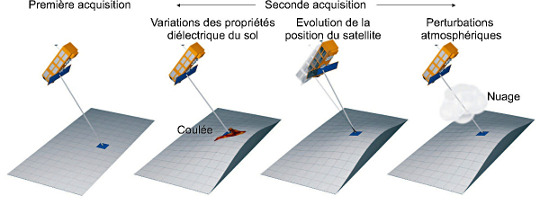
Le calcul de la différence des phases entre l'image maitresse (celle de la première prise de vue) et esclave (celle de la seconde prise de vue) de sorte à en déduire la déformation peut être entaché de certaines erreurs. Ces erreurs sont de plusieurs ordres et peuvent affecter soit la valeur de la phase pixellaire, soit la valeur de la phase de trajet (cf. figure 4).
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 12. Sources d'altération de la phase mesurée
Lors de la première acquisition, le satellite enregistre la valeur de la phase du signal rétrodiffusé. Cette valeur enregistrée dépend de la phase pixellaire et de la distance parcourue par le signal. La seconde acquisition peut être perturbée par différents processus.
Variation de la nature du sol. Cela impacte la phase pixellaire. Si la nature du sol change, alors la phase pixellaire change, la valeur de phase enregistrée dépendra des changements des propriétés du sol en plus des variation de distance entre sol et satellite.
Variation de la position du satellite. Le satellite ne peut pas revenir exactement à la même position lors de la seconde acquisition, ce qui modifie la phase de trajet. La distance parcourue n'est donc plus la même entre les deux acquisitions. C'est ce type d'artéfact qui est recherché pour calculer des MNT[2] plutôt que mesurer la déformation.
Variation des conditions atmosphériques. L'atmosphère peut perturber la valeur de la phase de trajet.
Variations de la phase pixellaire et cohérence
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
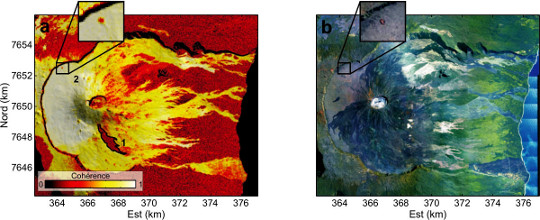
Figure 13. Cohérence et variations de la phase pixellaire
a : carte de cohérence d'un interférogramme couvrant la période du 01/09 au 26/10/2010. ; b : mozaïque de photos aériennes.
La cohérence est équivalente à un calcul de variance sur l'interférogramme calculé : plus la différence des phase est similaire pour des pixels contigus, plus l'interférogramme est dit cohérent. Une forte cohérence indique que la nature du sol a peu changé entre les deux acquisitions, une faible cohérence témoigne d'un changement de la nature du sol. Sur cette image de cohérence, les pertes de cohérence sont dues à différents processus.
Variation de la végétation. Visible sur toute la partie Est, très végétalisée, la végétation change de disposition (croissance, variations saisonières...), ce qui modifie la phase pixellaire entre les deux acquisitions, et qui donne l'impression d'un signal bruité dans ces zones. L'intensité de la perte de cohérence est liée à la longueur d'onde utilisée (très sensible pour des longueurs d'ondes proches de la taille des objets variables : ENVISAT est sensible aux variations saisonnières, ALOS l'est moins, cf. figure 8). Ici les zones très cohérentes correspondent à des zones couvertes par des coulées de lave antérieures à la première prise de vue mais non encore végétalisées, donc montrant une forte cohérence du fait de l'absence de variabilité végétale.
Coulées de lave. La zone notée 1 est une coulée de lave mise en place entre la première et la seconde acquisition. La nature du sol a complètement changé, la phase pixellaire n'est plus du tout la même entre les deux images.
Variation de la nature du sol. L'encart noté 2 correspond à un cône de scorie très visité par les promeneurs (nommé Formica Leo), leur passage répétitif modifie la répartition des scories au sol, ce qui perturbe la phase pixellaire.
Variations de la position du satellite
Toute variation de la position du satellite entre les deux acquisitions s'accompagne d'une modification de la phase de trajet. Ce principe peut être utile pour mesurer l'altitude d'une zone (SRTM – campagnes de mesures topographiques, par exemple) mais constitue un signal parasite dans la mesure de la déformation.
Le calcul d'un interférogramme de mesure de déformation nécessite de connaitre la différence des positions d'acquisition entre les deux dates de sorte à simuler les franges liées à cette différence de position et à les retrancher de l'interférogramme de départ. Plus le modèle numérique de terrain (MNT) utilisé sera proche de la topographie réelle, meilleures seront les corrections.
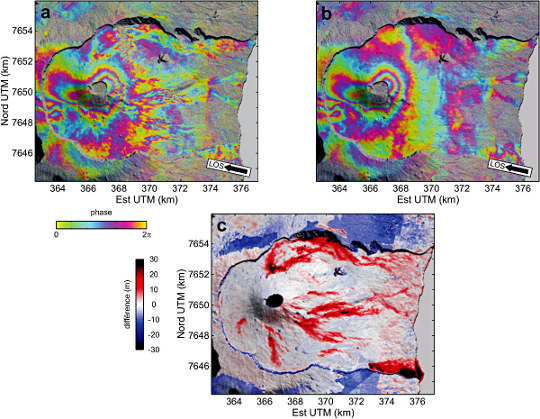
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 14. MNT et correction des biais induits par les variations de la position du satellite
a : interférogramme calculé avec un MNT ancien. b : le même interférogramme calculé avec un MNT récent. c : différence entre les deux MNT.
Sur l'interférogramme de gauche, beaucoup de petites franges parasites sont visibles mais ne le sont plus sur l'interférogramme de droite. Ces franges parasites correspondent à des résidus topographiques non corrigés, liés à la l'accumulation de coulées de lave postérieures au relevé du premier MNT. Ces résidus sont d'autant plus importants que la coulée est épaisse. Le cône central s'est effondré en 2007, avec une différence d'altitude de plus de 300 m.
Effets atmosphériques
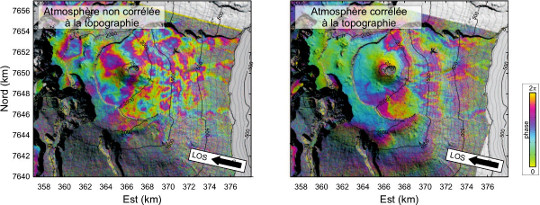
Les variations des conditions atmosphériques entre les deux acquisitions sont source de deux types de signaux parasites : les signaux corrélés à la topographie (à l'altitude du sol) et ceux qui ne le sont pas. En effet, l'épaisseur de la couche atmosphérique traversée par les ondes radar est d'autant plus faible que l'altitude du sol est élevée.
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 15. Deux types de perturbations atmosphériques
Deux interférogrammes couvrant chacun une période différente de 35 jours et n'ayant pas subi de déformation. À gauche, perturbations non corrélées à la topographie : les franges sont dues, par exemple, à des variations de densité de l'atmosphère due à des nuages plus ou moins chargés en eau. À droite, perturbation corrélée à la topographie. Les franges suivent les lignes de niveau. Ce type d'artéfact a lieu lorsque l'atmosphère est stratifiée avec peu de turbulences.
Les signaux corrélés à la topographie peuvent parfois être corrigés, alors que les signaux liés à une atmosphère turbulente sont plus difficiles à corriger et nécessitent d'avoir des images météo rarement disponibles à résolution suffisante et au moment adéquat.
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
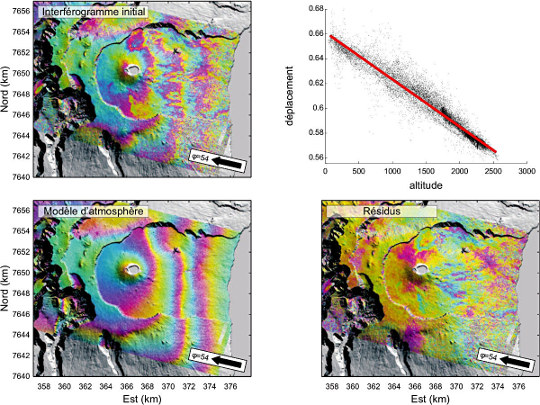
Figure 16. Exemple de correction d'atmosphère corrélée à la topographie
Le graphique (en haut à droite) correspond à la corrélation entre le déplacement mesuré et la topographie. On y voit une relation linéaire. Cette relation linéaire permet de construire un modèle d'atmosphère (en bas à gauche) qui sera retranché de l'image de départ (en haut à gauche). Sur l'image corrigée (en bas à droite), on observe la présence de petites franges qui correspondent à des résidus topographiques (non corrigés du fait de la mise en place de coulées de laves postérieurement au relevé du MNT utilisé, cf. figure 14).
Une fiche de synthèse
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
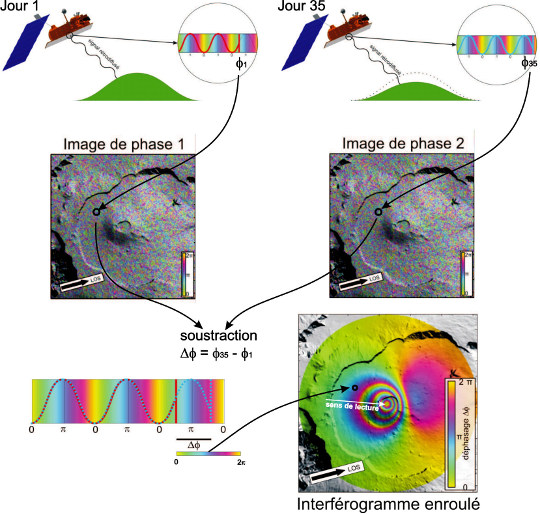
Figure 17. Principes de l'interférométrie radar (InSAR)
- Le jour 1, le satellite enregistre pour chaque pixel, la valeur de la phase (entre 0 et 2π ) du signal rétrodiffusé.
- Le jour 35, le satellite revient exactement à la même position et enregistre de nouveau une image de phase. Si le sol a bougé entre les deux acquisitions, la valeur de la phase pour chaque pixel ne sera pas la même.
- Pour chaque pixel, on calcule le déphasage entre les deux dates (différence entre les deux valeurs de phase). Pour les zones n'ayant pas bougé, ou ayant bougé d'un multiple de la longueur d'onde, la valeur sera de 0, ce qui fait apparaître des franges sur l'interférogramme.
Pour déterminer le sens des déplacements :
- on part d'un endroit qui n'a pas bougé,
- puis on suit l'ordre des couleurs vers un endroit qui a beaucoup bougé (flèche blanche),
- l'ordre de passage des couleurs donne alors le sens du mouvement : phase qui augmente (respectivement diminue) correspond à éloignement (respectivement rapprochement) par rapport au satellite dans la direction de la ligne de visée.
Ici, dans la figure ci-dessus, on part du vert, puis on passe au rose, puis au jaune, puis au vert, puis au rose.... : la valeur de la phase augmente, la distance sol-satellite a donc augmenté, et comme le satellite est fixe, c'est le sol qui s'est éloigné. Il s'agit dans cet exemple d'un signal compatible avec une subsidence.
Que fait-on des données d'interférométrie radar ?
Les interférogrammes permettent d'obtenir des cartes de la déformation. L'utilisation la plus commune des interférogrammes est la recherche des sources à l'origine de la déformation. Dans le cas d'un volcan, une source de déformations de surface pourra, par exemple, être le remplissage / la vidange d'un réservoir magmatique dont on ne connaît ni la taille ni la profondeur. Généralement, ces sources sont cherchées par “essai/erreur” : on teste plusieurs géométries différentes, et on garde celle(s) permettant de reproduire au mieux la déformation. On dit qu'on « inverse » le problème. En effet, on sait calculer les déplacements engendrés par une source connue, mais il est difficile de trouver la source connaissant les déplacements. Les inversions permettent de quantifier les paramètres de la source (quantité de glissement sur une faille, variation de volume d'une chambre magmatique …).
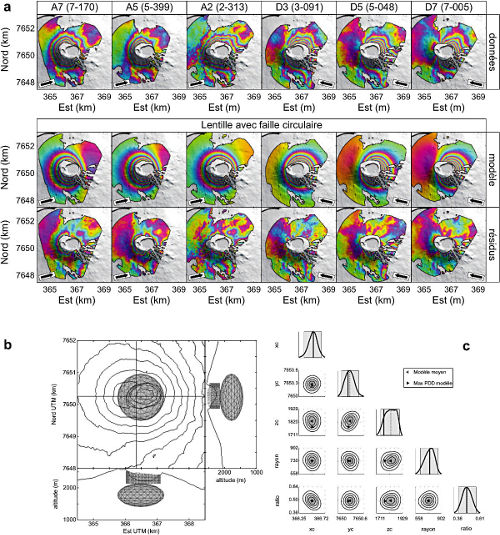
Les modèles utilisés se basent sur des aprioris, qu'il est nécessaire de confronter à d'autres données (terrain, télédétection...). La figure 18, ci-dessous, montre le résultat d'une inversion sur des données acquises suite à l'effondrement du cratère Dolomieu (Piton de la Fournaise) lors de l'éruption d'avril 2007. Les résultats montrent une position de la source beaucoup trop superficielle pour correspondre à une chambre magmatique. Des données complémentaires de mesures thermiques, des observations de terrain mettant en évidence de nombreuses fumerolles permettent d'interpréter cette source comme un système hydrothermal en cours de drainage suite à l'effondrement.
Source - © 2019 A. Augier - OPGC / CC BY-SA 4.0
Figure 18. Exemple d'utilisation des données InSAR : l'inversion
On dispose de 6 interférogrammes dans des géométries d'acquisition différentes, couvrant les déplacements post-éruptifs du cône central du Piton de la Fournaise après l'éruption d'avril 2007. Les résultats du meilleur modèle sont reprojetés dans la géométrie de chaque acquisition. Pour juger de la qualité de l'inversion, on présente souvent une image de résidus, c'est-à-dire la différence entre les données et le modèle. Moins il y en a, meilleur est le modèle. Ici, deux sources ont été prises en compte : une source lenticulaire et une fracture cylindrique. La source lenticulaire est trouvée à haute altitude, ce qui exclut que ces déplacements soient dus à une chambre magmatique. Ils sont interprétés comme un système hydrothermal « percé ». Les courbes de droite montrent les incertitudes des paramètres inversés.
L'interférométrie radar sert à mesurer des déplacements. Dans le domaine géologique, citons sous forme d'un inventaire non-exhaustif : les déplacements dus aux phénomènes volcaniques (comme montrés dans cet article), les déplacements tectoniques sismiques ou asismiques (cf. Le séisme du 11 novembre 2019, Le Teil (Ardèche)), les variations d'épaisseur des glaciers, les glissements de terrains, des subsidences liées à des pompages excessifs de nappes phréatiques… Mais ceci mérite, en plus de cet article consacré aux principes de l'InSAR, un article dédié à ses diverses applications.
Bibliographie
Aurélien Augier, 2011. Étude de l'éruption d'avril 2007 du Piton de la Fournaise (île de la Réunion) à partir de données d'interférométrie RADAR et GPS, développement et application de procédures de modélisation, Univ. Clermont-Ferrand 2, thèse de doctorat
Jean-Luc Froger, Vincent Famin, Valérie Cayol, Aurélien Augier, Laurent Michon, Jean-François Lénat, 2015. Time-dependent displacements during and after the April 2007 eruption of Piton de la Fournaise, revealed by interferometric data, Journal of Volcanology and Geothermal Research, 296, 55-68 (pdf sur HAL)
Site du Service OI2 (InSAR Observatory of Indian Ocean), Observatoire de Physique du Globe de Clermont-Ferrand (OPGC)
Les pages “InSAR” du site www.kunos.fr