Article | 20/02/2020
Corrélation d'images – Principes et utilisation dans la surveillance de la déformation du sol
20/02/2020
Résumé
Comparaison systématique d'images pour cartographier point par point les déplacements et obtenir une image de déformation entre deux états.
Table des matières
Introduction
Cet article présente les principes de la corrélation d'images et son utilisation pour la surveillance de la déformation du sol. La compréhension de la technique nécessite d'avoir quelques bases sur la structure d'une image numérique, mais rien de très technique : un élève de première au lycée peut tout à fait comprendre cette méthode.
La corrélation d'images est plus qu'une “simple” comparaison d'images pour, par exemple, suivre “grossièrement” l'avancée ou le recul du front d'un glacier à l'aide de photographies aériennes, cartes topographiques, et/ou images satellitaires (cf. La Mer de Glace : grandeur (et décadence ?) d'un glacier alpin, La disparition d'un glacier alpin : l'ex glacier des Prés les Fonts, le Monêtier-les-Bains (Hautes Alpes), ou encore Icebergs et variations climatiques dans les Alpes), comparaison menée sur table ou sur Google Earth ou équivalent (cf. Quelques outils cartographiques "français" disponibles en 2017 pour l'enseignement des Sciences de la Terre). L'objectif de cet article est de donner les principes de base permettant de lire et comprendre des images obtenues par corrélation d'images.
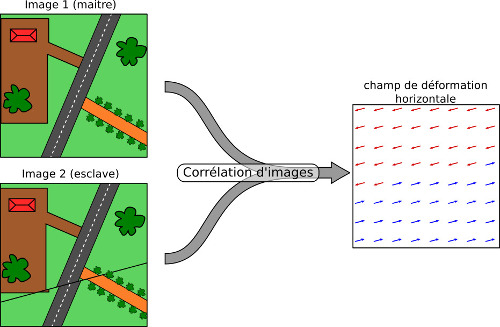
La mesure de la déformation par corrélation d'images a pour but de comparer deux images d'une même zone prises, généralement, par un satellite à deux moments différents, puis à rechercher dans la seconde (appelée image esclave) la position de points de repères présents dans la première image (appelée image maitre). Si la position du point de repère n'est pas la même, c'est que le sol a bougé.
Comme on connait la résolution de l'image (taille en mètres d'un pixel) il est alors possible de revenir à la quantité de déplacement dans les composantes horizontales (vers l'Est et vers le Nord) en comparant la position d'un objet dans les deux images. Cependant, comme le satellite vise globalement à la verticale, cette méthode ne permettra pas d'avoir accès à la composante verticale de la déformation, et seule la composante horizontale sera accessible.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 1. Principes de la corrélation d'images
En comparant deux images satellites, il est possible de revenir au champ de déformation de la zone étudiée en comparant la position de différents objets sur les deux images. L'exemple est donné ici pour une faille décrochante senestre (quand on se positionne sur l'un des blocs, l'autre se déplace vers la gauche par rapport à nous).
On verra dans un premier temps comment chercher un fragment d'image dans une autre image, puis, en se basant sur un modèle analogique de remplissage d'un réservoir, comment cette recherche est adaptée à la mesure de la déformation. Enfin, on discutera des conditions d'utilisation de cette technique.
Recherche de la position d'un fragment d'image dans une image
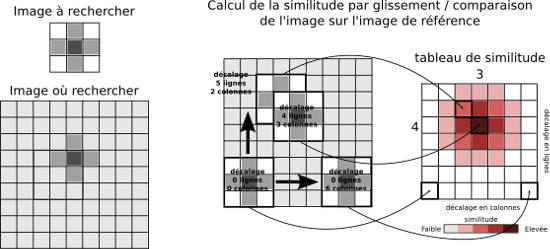
Pour chercher la position la plus probable d'un fragment d'image dans une image (dite image maitre), il suffit de faire glisser en ligne et en colonne le fragment sur l'image de référence, puis pour chaque décalage, de comparer les valeurs des pixels entre le fragment et l'image. Plus la différence est faible, plus la position du fragment dans l'image maitre est probable.
On peut donc déterminer un tableau de similitude qui permet de répertorier la similitude entre le fragment et l'image maitre pour chaque décalage. La figure 2 montre les principes de cette recherche.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 2. Recherche de la position d'un fragment d'image dans une autre
On cherche à retrouver la position de la petite image dans la grande. Pour ceci, on fait glisser la petite image dans la grande, et pour chaque décalage en pixels (ligne et colonne) on calcule un indice de similitude. Ces indices sont rangés dans un tableau. La valeur extrémale du tableau donnera le décalage en pixels (lignes et colonnes) pour lequel la position de la petite image est la plus probable.
L'indice de similitude peut par exemple être calculé en sommant pour chaque décalage, la valeur absolue des différences des valeurs des pixels entre l'image à chercher et la zone de l'image dans laquelle on cherche (méthode des moindres carrés). Les valeurs sont rangées dans un tableau, qui contiendra moins de lignes et de colonnes que l'image de départ. En effet, dans notre cas l'image complète comporte 9 lignes et 9 colonnes, il n'est possible de décaler la petite image à rechercher, de 3×3 pixels, que de 6 lignes et 6 colonnes dans l'image de référence, il n'existe donc que 7×7=49 positions possibles de l'image à rechercher dans l'image de référence.
Application à la mesure de la déformation : exemple sur un modèle analogique
Montage expérimental et images
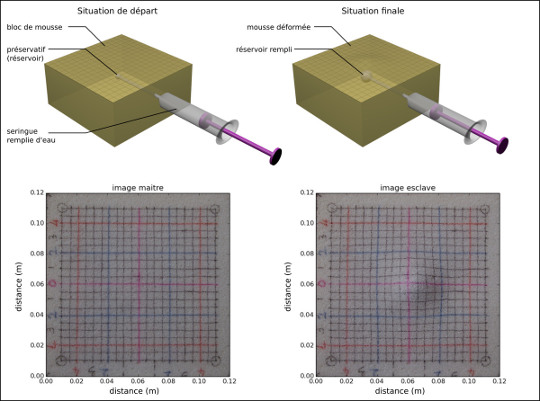
L'exemple d'application ci-dessous n'est pas fait avec des images satellites, mais à partir de photographies d'un bloc de mousse dans lequel a été injecté du liquide afin de simuler la déformation liée, par exemple, au remplissage d'un réservoir volcanique. La première image est prise avant le remplissage, la seconde est prise après.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 3. Montage du modèle analogique
On insère dans un bloc de mousse un tuyau relié à un préservatif servant de réservoir et à une seringue à l'extérieur du bloc de mousse. Le réservoir est rempli, ce qui provoque une déformation de la surface du bloc de mousse. Une photo de la surface de la mousse est prise avant le remplissage, une autre après. Les motifs sur le bloc de mousse ne servent qu'à permettre d'avoir un aspect hétérogène de la surface. N'importe quel motif permettrait d'obtenir des mesures équivalentes.
Mesure de la déformation pour un point
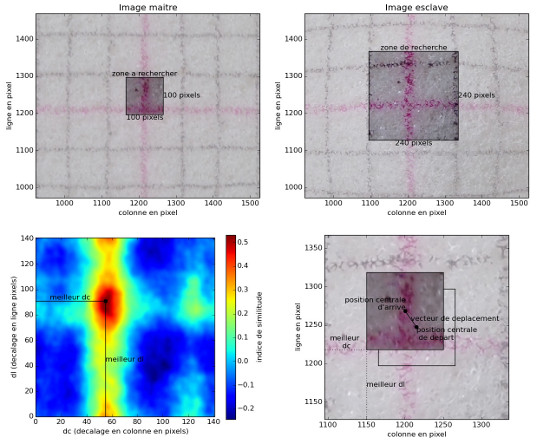
La mesure de la déformation consiste à retrouver des fragments de la première image dans la seconde. Afin d'accélérer le calcul, et comme les processus géologiques provoquent des déformation rarement supérieures à 20 mètres, la recherche est limitée à une partie de la seconde image.
Source - © 2019 A. Augier / CC BY-SA 4.0
Figure 4. Obtention d'un vecteur de déformation
On sélectionne une petite zone de l'image maitre (la première), puis on recherche sa position la plus probable sur l'image esclave (la seconde). Cette recherche est faite en faisant glisser un extrait de l'image maitre sur un extrait plus grand de l'image esclave, et en calculant un indice de similitude pour chaque décalage en ligne et en colonne comme indiqué en figure 2. Le meilleur décalage en ligne est noté “dl”, le meilleur décalage en colonne est noté “dc”. Il est alors possible de retrouver le vecteur de déplacement entre les deux images.
Le décalage pour lequel l'indice de similitude est le plus fort nous donnera la position de l'extrait de l'image maitre dans l'extrait de l'image esclave. On obtient ainsi le déplacement horizontal (en pixels, dans l'axe est/ouest et dans l'axe nord/sud) de la zone d'intérêt entre les deux images. Comme on connait la taille réelle d'un pixel, il est facile de revenir aux déplacements en mètres.
Représentations du champ de déformation
L'opération de recherche de zones par corrélation d'images est répétées pour plusieurs zones de l'image, ce qui permet d'obtenir un vecteur de déplacement par zone, et donc un champ de déformation. Les images suivantes montrent différents moyens de représenter la déformation. Ces différentes représentations donnent la même information, mais les chercheurs peuvent adopter telle ou telle représentation en fonction de l'objet étudié ou de leurs préférences.
Source - © 2019 A. Augier / CC BY-SA 4.0
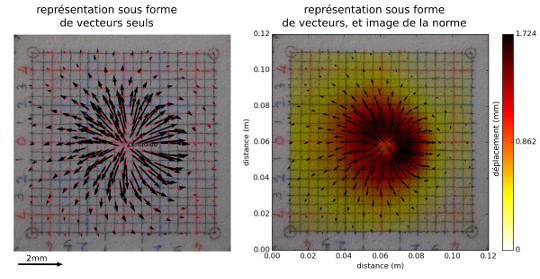
Figure 5. Représentation sous forme de vecteurs
La représentation de gauche montre les vecteurs de déformation obtenus pour chaque opération de corrélation. Le centre de chaque extrait d'image est indiqué par un point rouge. La représentation de droite ajoute une image interpolée de la norme des vecteurs : chaque point rouge est remplacé par un point dont la couleur indique la norme du vecteur de déformation, ce qui dessine par interpolation des “courbes de niveau” de déformation sur lesquelles se base la colorisation complète de l'image.
Pour les deux représentations, l'image maitre a été incrustée en arrière plan.
Source - © 2019 A. Augier / CC BY-SA 4.0
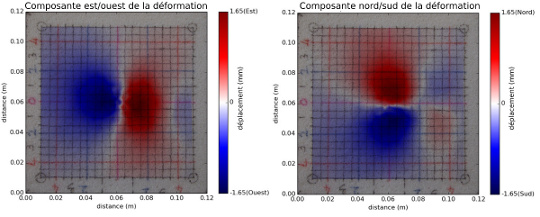
Figure 6. Représentation sous forme de composantes du vecteur de déformation
Pour chaque vecteur de déformation on considère uniquement sa composante Est/Ouest ou Nord/Sud et on représente son sens par une couleur (bleu = vers l'Ouest / le Sud ; rouge vers l'Est / le Nord), et sa norme par l'intensité de la couleur (de blanc pour une norme nulle à une couleur de plus en plus foncée).
La représentation de gauche montre la composante Est/Ouest du vecteur de déformation, celle de droite la composante Nord/Sud. Ici, les vecteurs ou leurs composantes ne sont pas représentés, seules apparaissent les images interpolées et l'image maitre (la situation initiale).
On remarque que la déformation est globalement axi-symétrique et centrifuge (intensité décroissante depuis une zone centrale). Sur la droite des images ci-dessus, on observe un second motif de déformation, qui est localisé au niveau du tube permettant le remplissage du réservoir. Ceci est dû au fait que le tube introduit une hétérogénéité, qui modifie localement les propriétés mécaniques de la mousse.
Par ailleurs, la zone se déformant le plus dans l'absolu est située au-dessus du réservoir. Cependant, la déformation y est verticale, et n'est donc pas visible par corrélation (pas de décalage latéral des pixels). La représentation avec la norme des vecteurs (figure 5) montre un motif annulaire, qui témoigne de cette absence de mesure de la composante verticale de la déformation.
Conditions d'utilisation de la corrélation d'image
Mesure de la déformation pour un point
Plusieurs paramètres sont à prendre en compte pour l'acquisition des images utilisées pour la mesure de la déformation par corrélation d'images.
- Saison. L'alternance des saisons peut poser certains problèmes pour la mesure de la déformation : si les deux images ne sont pas acquises dans des conditions proches, la corrélation sera difficile à faire. En effet, l'état de la végétation aboutira à des aspects très différents des deux images, mais aussi les ombres des objets (arbres, reliefs) n'auront pas la même taille ni la même orientation.
- Jour/nuit. Les images ne peuvent être acquises que de jour : contrairement au images radar, les satellites utilisés pour la corrélation d'images sont des satellites dits passifs, qui récupèrent la lumière du Soleil réfléchie par le sol. Il est techniquement possible de faire de la corrélation sur des images radar, mais la résolution de ces images est beaucoup plus faible que celle des satellites optiques, et seules de très grandes déformations pourraient être mesurées ainsi.
- Météo. La présence de nuages empêche de faire des mesures par corrélation d'images. L'ombre des nuages au sol peut aussi altérer la qualité de la mesure.
Résolution de la mesure de la déformation
Plusieurs paramètres techniques règlent la résolution finale de la mesure.
- Résolution spatiale des points de mesure. La résolution spatiales dépend du nombre de fragments d'images utilisés pour les calculs (voir figure 4). Dans le meilleur des cas, elle est égale à la résolution des images de départ (on réalise autant de fragments d'images, et donc de vecteurs de déformation, que de nombre de pixels). Pour les meilleurs satellites optiques, elle peut atteindre 1 m (0,7 m pour les satellites du système Pléiades).
- Résolution de la mesure de la déformation. La comparaison entre les images se faisant en décalant d'un pixel à chaque fois, la résolution de la mesure de la déformation sera de l'ordre de grandeur de la résolution des images, soit environ 1 m pour les meilleurs satellites. Il est possible d'améliorer la résolution en sur-échantillonnant les images (c'est-à-dire en augmentant artificiellement le nombre de pixels, chaque pixel étant par exemple découpé en 4 pixels (ou plus) de même valeur). Ainsi, on peut arriver à mesurer au mieux des déformations de l'ordre de la dizaine de centimètres, ce qui limite beaucoup le champ d'application de cette méthode.
- Résolution temporelle. La résolution temporelle dépend du temps de revisite de la zone d'intérêt par le satellite. Elle est d'au mieux un jour pour les satellites tels que Pléïades, à condition que les conditions météorologiques le permettent. Il est cependant possible de faire des mesures par comparaison d'images provenant de satellites différents, ce qui peut permettre d'améliorer la résolution temporelle, à condition de ré-échantillonner les images prises par les différents satellites, de sorte à uniformiser leur résolution (on se ramène à la plus basse des résolutions spatiales disponibles).
- Caractérisation du vecteur de déformation. La technique se basant sur un décalage latéral des pixels, elle ne permet qu'une mesure des composantes horizontales de la déformation (Est/Ouest et Nord/Sud, par exemple). Elle peut donc être utilisée en complément de l'interférométrie radar (accès à la composante verticale) ou du GPS [global positioning system ou géo-positionnement par satellite] (mesure des trois composantes, mais pour un seul point).
Objets géologiques surveillés
À cause de la mauvaise résolution de la mesure de la déformation, seuls les événements provoquant des déformations d'au moins l'ordre du mètre sont suivis. Il s'agit principalement des grands séismes (figure 8), des glissements de terrain, mais aussi du suivi de déplacements des glaciers (figure 7).
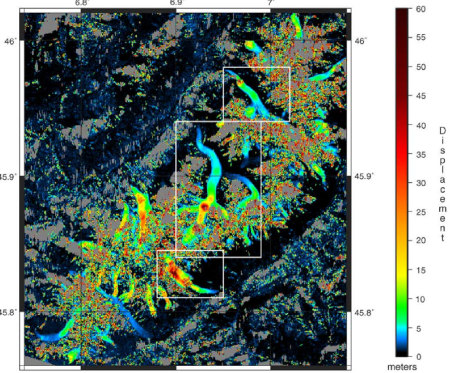
Source - © 2005 D'après Berthier et al. [1], modifié
Figure 7. Suivi du déplacement de différents glaciers du Mont Blanc obtenu par corrélation d'images
Sur cette image, seule la norme des vecteurs de déformation est montrée. On voit que la déformation des glaciers, liée à leur écoulement, n'est pas homogène sur leur longueur.
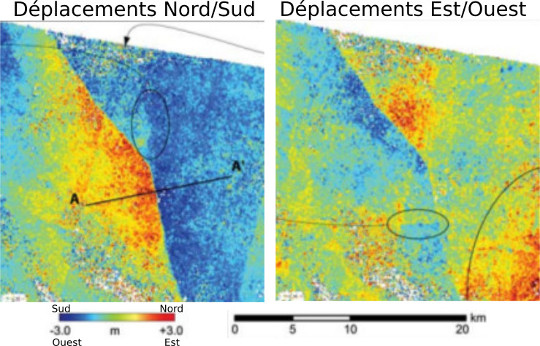
Source - © 2007 D'après Leprince et al. [2], modifié
Figure 8. Déformation due au séisme d'Hector Mine (Californie, 1999)
Les auteurs ont choisi une représentation des composantes de la déformation plutôt que les vecteurs. Il s'agit ici d'un séisme décrochant, le bloc Ouest partant vers le Nord-Ouest (M 7.1 - 16km SW of Ludlow, CA – 1999-10-16). La faille correspond au contact entre zones se déplaçant en sens opposés.
La déformation liée à des remplissages/vidanges de réservoirs (volcans, pompages) n'est pas suivie par corrélation d'images car de trop faible amplitude. On préférera alors l'InSAR (cf. Interférométrie radar : principes et utilisation dans la surveillance de la déformation du sol) ou le GPS (cf. La physique et le GPS ou, sur le site CS-Physique, Le GPS - Principe de localisation dans l'espace (1/2)).
Calculs et codage Python en classe
Les calculs de corrélation d'images peuvent être mis en œuvre relativement facilement dans le cadre de projets informatiques au lycée comme en CPGE, avec des élèves motivés. Les exemples donnés pour le modèle analogique ont été traités à l'aide de fonctions usuelles des modules numpy et matplotlib de Python. Les images ont été acquises à l'aide d'un appareil photo reflex numérique (un premier prix) sans pied, elles ont été recalées au niveau de points de repères visibles dans les coins des images (recalage fait sous Python, mais faisable avec le logiciel GIMP). Les algorithmes ont été essayés avec succès sur des photos prises avec un téléphone portable, ce qui permet d'envisager une utilisation en classe. Un fichier python-corr-images.zip est proposé au téléchargement ; il contient 2 images (maitre - esclave du type de celles de la figure 3) et deux codes Python largement commentés, l'un pour calculer un vecteur déplacement sur un extrait de l'image, l'autre, répétant en boucle le premier, pour effectuer le calcul sur une grille régulière et créer une image complète de déplacement.
Bibliographie
E. Berthier, H. Vadon, D. Baratoux, Y. Arnaud, C. Vincent, L. Feigl, F. Rémy, D. Legrésy, 2005. Surface motion of mountain glaciers derived from satellite optical imagery, Remote Sensing of Environment, 95, 1, 14-28 [pdf]
S. Leprince, S. Barbot, F. Ayoub, J.-P. Avouac, 2007. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements, IEEE Transactions on Geoscience and Remote Sensing, 45, 6, 1529-1558 [pdf]
La page “Corrélation d'images” du site www.kunos.fr