Subsidence initiale, subsidence thermique et déformations au cours du rifting continental

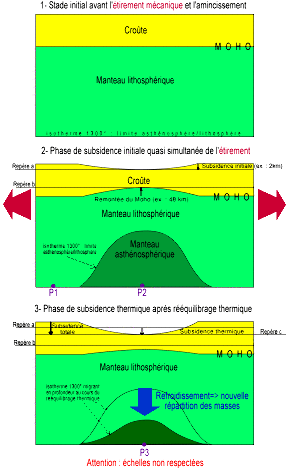
La dénomination de subsidence initiale (ou subsidence tectonique) suivie de subsidence thermique dérive des idées de Mc Kenzie (1978), qui a proposé un « modèle thermique d'amincissement uniforme de la lithosphère ». Même si d'autres modèles plus précis et plus complexes lui ont succédé, celui de McKenzie reste toujours une représentation valide et simple de l'extension.

Ce modèle repose sur deux phases successives :

La subsidence finale totale est la somme de la subsidence initiale (ou tectonique) et de la subsidence thermique.

Figure 1. Représentation schématique des différentes phases de subsidence faisant suite à un amincissement homogène de la lithosphère

La lithosphère est soumise à un étirement et s'amincit donc. En particulier, la croûte, pouvant être considérée comme un "flotteur" car moins dense que le manteau, est amincie. De plus, l'asthénosphère remonte. Si ces modifications dans la répartition des masses sont assez lentes (quelques cm/an), elles induisent, de façon quasi contemporaine à cette phase d'étirement, un réajustement isostatique (de manière à maintenir l'égalité des pressions P1 et P2). Ce réajustement isostatique conduit à une « subsidence initiale » (ou « subsidence tectonique »). Puis, au fil du temps, l'asthénosphère qui était remontée se refroidit et devient donc de la lithosphère, plus dense. Ce rééquilibrage thermique induit un réajustement isostatique étant donné que l'épaisseur de la couche la plus dense, la lithosphère mantellique, augmente (on doit retrouver P1 = P2 = P3). Ce réajustement isostatique lié au rééquilibrage thermique est à l'origine lui aussi d'une subsidence, la « subsidence thermique ».

Voir plus loin, pour en savoir plus sur les hypothèses du modèle de McKenzie.

Deux phénomènes, souvent mis en opposition, peuvent être à l'origine de l'amincissement initial et donc de la subsidence :

Poser la question des causes de cette extension est très délicat. Est-ce que la déformation de la lithosphère (à cause du champ de contrainte régional ou local) induit la remontée de l'asthénosphère ou est-ce que l'apparition d'une anomalie thermo-mécanique (due à des causes internes, panache...) induit un bombement puis la déformation de la lithosphère et la fracturation de la croûte ? Même si, théoriquement, il est possible d'analyser en surface les flux de sédimentation pour savoir si le bombement thermique précède ou suit la fracturation de la croûte, la réponse n'est pas toujours évidente.

Voir l'exemple d'une étude sur le terrain : le cas du rift de Limagne (Excursion d'une journée en Limagne ou Découvrir et comprendre le rift de la Limagne). Quoiqu'il en soit l'extension de la lithosphère et en particulier la fracturation de la croûte est l'expression des contraintes présentes dans la lithosphère.

Lorsque l'épaisseur de la lithosphère diminue de façon instantanée à l'échelle des temps géologiques, l'équilibre isostatique est rompu. L'équilibre isostatique correspond à l'équilibre hydrostatique des physiciens. La Terre se comportant comme un fluide sur des échelles de temps géologiques, elle est en équilibre hydrostatique (tel un fluide). Chaque colonne verticale depuis la surface jusqu'à un niveau de compensation (généralement situé dans le manteau) doit avoir le même poids. La méthode consiste à comparer deux colonnes de section unité avant et après déformation. Maintenir l'équilibre isostatique revient donc à compenser la perte de masse (liée à l'amincissement) par des apports d'asthénosphère de masse équivalente. Comme l'asthénosphère (densité de 3,25) est plus dense que la lithosphère (densité "pondérée" prenant en compte les densités de 3,3 - densité du manteau lithosphérique - et de 2,7 - densité de la croûte continentale), le volume d'asthénosphère qui compense la perte de masse lithosphérique est plus faible que le volume de lithosphère disparu. Il en résulte une subsidence de la surface (voir les exemples de quantification de la subsidence initiale).

La subsidence initiale est donc directement liée au maintien de l'équilibre isostatique à la suite d'un amincissement lithosphérique.

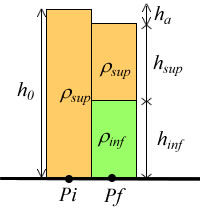
On note : h les épaisseurs, ρ les masses volumiques considérées comme constantes pour une couche donnée. Les indices a, sup, inf correspondent respectivement à l'air, à la couche supérieure et la couche inférieure. h_a est donc la profondeur de la dépression formée à la suite de l'étirement de lithosphère. h_inf correspond à la remontée de la couche inférieure. Surface de compensation : toutes les pressions exercées sur cette surface sont égales.

Figure 2. Principe de l'isostasie

On écrit l'égalité des pressions lithostatiques sur la surface de compensation : P_i = P_f soit ρ_supgh₀ = ρ_infgh_inf + ρ_supgh_sup + ρ_agh_a avec g l'accélération de pesanteur. On tient compte de ρ_a = 0 (attention, dans le cas d'un remplissage par l'eau et/ou les sédiments, il faudrait tenir compte de leur densité). On simplifie par g. On obtient alors :

Connaissant l'amincissement β, c'est-à-dire le rapport h₀/ h_sup, on calcule aisément h_inf en fonction de h₀ :

Connaissant alors h_sup, h₀ (ou β et h₀), on en déduit :

Applications numériques

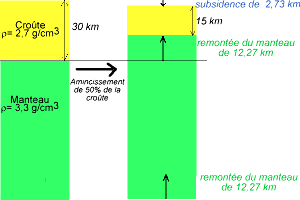
Cas 1 : amincissement de la croûte seule, calcul de la subsidence induite

Ce premier cas (figure 3) est très simplifié car on ne considère qu'un modèle à deux couches de densité différentes (croûte continentale ρ = 2,7 g/cm³ et manteau ρ = 3,3 g/cm³) en négligeant donc la différence entre lithosphère et asthénosphère. C'est le genre de calcul réalisé par Airy dès le milieu du 19^ème siècle. C'est une bonne approximation de premier ordre puisque la différence de densité entre la croûte et le manteau (0,6) est en gros dix fois supérieure à la différence de densité entre le manteau asthénosphérique et le manteau lithosphérique (0,05). La couche inférieure est le manteau ρ_inf = 3,3 g/cm³, la couche supérieure est la croûte continentale ρ_sup = 2,7 g/cm³.

Dans le cas d'un amincissement de h₀ - h_sup = 1 km, on trouve une remontée du manteau h_inf = 818 m et une subsidence h_a = 181 m.

Dans le cas d'un amincissement de 50% d'une croûte de 30 km d'épaisseur (h₀ = 30 km et h_sup = 15 km, on trouve une remontée du manteau h_inf = 12,27 km et une subsidence h_a = 2727 m.

Figure 3. Amincissement de 50% de la croûte et subsidence tectonique associée

Cas 2 : amincissement de la lithosphère seule, cas des dorsales

Ce deuxième cas (figure 4) est aussi une approximation, puisqu'il ne fait varier que l'épaisseur du manteau lithosphérique ( ρ = 3,3 g/cm³) reposant sur un manteau asthénosphérique (ρ = 3,25 g/cm³) et néglige la présence de croûte ou suppose qu'elle ne varie pas d'épaisseur. Cela ne représente que le cas d'une dorsale, où il y a effectivement variation d'épaisseur de la lithosphère sans variation d'épaisseur de le croûte (épaisseur très faible, toujours de 6 à 8 km).

La couche inférieure est le manteau asthénosphérique ρ_inf = 3,25 g/cm³. La couche supérieure est le manteau lithosphérique ρ_sup = 3,3 g/cm³.

Dans le cas d'un amincissement de 1 km de ce manteau lithosphérique soit h₀ - h_sup = 1 km. On trouve une remontée du manteau h_inf = 1,0154 km, on a donc un bombement d'environ 15,4 m par rapport à la situation avant amincissement.

Sous une dorsale, on a 0 km de manteau lithosphérique alors que sous une plaine abyssale, il est de 100 km. Une dorsale est donc 1.500 m plus haute qu'une plaine abyssale (sans compter l'effet de la dilatation due à la fusion partielle).

Figure 4. Absence de manteau lithosphérique et bombement tectonique associé

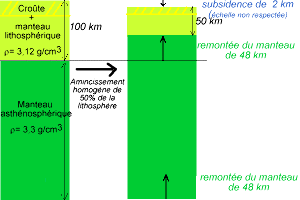
Cas 3 : amincissement simultané du manteau lithosphérique et de la croûte

Le troisième cas (figure 5) représente mieux la réalité continentale, avec une lithosphère composée de 30 km de croûte (ρ = 2,7 g/cm³) et de 70 km de manteau lithosphérique (ρ = 3,3 g/cm³), ce qui fait une lithosphère de densité moyenne de 3,12 g/cm³ ((30 x 2,7 + 70 x 3,3) / 100 = 3,12) surmontant une asthénosphère (ρ = 3,25 g/cm³).

La couche inférieure est le manteau asthénosphérique ρ_inf = 3,25 g/cm³. La couche supérieure est l'ensemble croûte + manteau lithosphérique ρ_inf = 3,12 g/cm³.

Prenons un amincissement de 50% de l'ensemble soit h₀ = 100 km et h₀ - h_sup = 50 km. On trouve une remontée du manteau h_inf = 48 km et une subsidence d'environ 2 km.

Figure 5. Amincissement homogène de 50% de la lithosphère et subsidence tectonique associée

Cette subsidence de 2 km résulte en fait :

• d'un effet crustal : -2.538,5 m (voir le cas 1 en prenant ρ = 3,25 g/cm³ pour le manteau sous-jacent avec un amincissement de 15 km de la croûte (ρ = 2,7 g/cm³) provoquant une subsidence de 2.538,5 m) ;
• d'un effet manteau lithosphérique : +539 m (voir le cas 2 : un amincissement de 35 km de manteau lithosphérique (ρ = 3,3 g/cm³) sur un manteau (ρ = 3,25 g/cm³) provoquant une remontée de 539 m).

En laissant le temps s'écouler, la partie supérieure de l'asthénosphère refroidira et deviendra lithosphère. En quelques dizaines de millions d'années, la lithosphère retrouvera son épaisseur standard de 100 km avec 15 km de croûte et 100 - 1 = 85 km de manteau. En effet, l'épaisseur de la croûte restera de 15 km car le Moho, la limite entre croûte et manteau, est une limite pétrographique. Par contre, la limite asthénosphère/lithosphère n'est qu'une limite thermique dans les péridotites mantelliques et le refroidissement de l'asthénosphère implique la migration de cette limite en profondeur, jusqu'à retrouver la situation initiale. Donc 50 km (85 km - 35 km) d'asthénosphère seront donc redevenus manteau lithosphérique, ce qui entraînera une subsidence thermique (très lente) de 770 m.

Le modèle de McKenzie insiste davantage sur l'évolution thermique d'une lithosphère soumise à une extension que sur les types de déformation engendrés. Faisons rapidement le point sur les conséquences d'un étirement sur l'évolution structurale de la lithosphère.

Au cours du rifting continental, la lithosphère est étirée et amincie. Cet étirement s'accompagne de déformations de la lithosphère. Le type de déformation dépend des propriétés rhéologiques de la roche. La roche peut se comporter de manière ductile (la déformation est continue) ou de manière cassante (la déformation est discontinue, par exemples des failles apparaissent). Pour une roche donnée, ses propriétés rhéologiques dépendent de la température et de la pression (donc de la profondeur). Si on considère une colonne de lithosphère, la profondeur limite entre le comportement ductile et le comportement cassant dépend du type de roche et du profil de température.

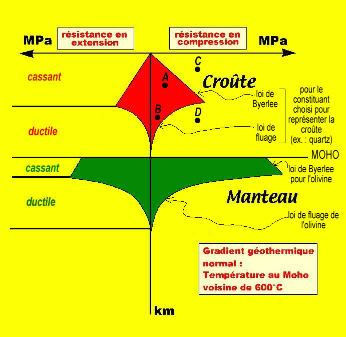
Figure 6. Profil rhéologique d'une lithosphère continentale

L'axe des abscisses correspond à la contrainte déviatorique (σ1-σ3) , différence entre contrainte maximale et contrainte minimale. L'axe des ordonnées correspond à la profondeur. La courbe indique l'intensité de la contrainte à partir de laquelle il y a déformation. En même temps, il permet de déterminer les types de déformation rencontrés dans une colonne de lithosphère.

Pour un état de contrainte et une profondeur donnés, le matériel ne se déforme pas ou le fait de manière élastique (réversible) tant que l'on reste à l'intérieur de la zone limitée par les droites de Byerlee et les courbes de ductilité (zone de résistance = zones rouges ou vertes) : cas des points A ou B. Dans la situation décrite par le point C, la croûte s'est déformée de façon cassante. Dans la situation du point D, la déformation de la croûte est ductile.

D'autre part, on remarque que les roches sont plus résistantes en compression qu'en extension.

Ce graphique est tracé en choisissant plusieurs paramètres.

Pour en savoir plus, voir le dossier CNRS sur les principes de la modélisation.

Comme il l'a été signalé au début, le modèle de McKenzie est un modèle simple basé sur un étirement symétrique et homogène dans la lithosphère. Certains modèles proches de celui de McKenzie font intervenir des déformations cassantes dans la croûte supérieure (avec apparition de failles et blocs basculés), la croûte inférieure s'étirant, elle, de manière ductile, tout comme le manteau lithosphérique. D'autres modèles, dérivés de ce premier placent des fractures dans la partie supérieure du manteau lithosphèrique, ce qui est le plus fidèle au profil rhéologique de la figure 6.

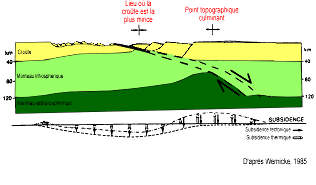
Mais il faut savoir qu'il existe également d'autres séries de modèles comme ceux de Wernicke ou de Lister qui font intervenir des failles de détachement (faille à pendage faible) traversant soit la lithosphère dans sa totalité, soit uniquement la croûte continentale supérieure. Ces modèles peuvent expliquer une asymétrie du rift et un décalage des zones d'amincissement maximal de la croûte et du manteau.(voir la figure 8 où le manteau asthénosphérique ne remonte pas à l'aplomb de la zone d'amincissement maximal de la croûte).

Figure 7. Modèle de Lister (1989) avec une faille de détachement affectant la croûte supérieure

La croûte inférieure et le manteau se déforment de manière ductile. L'amincissement de la croûte est asymétrique alors que celui du manteau est symétrique.

Figure 8. Modèle de Wernicke avec une faille de détachement affectant la lithosphère

L'amincissement de la lithosphère est asymétrique. La remontée maximale de manteau lithosphérique n'a pas lieu à l'aplomb de la zone d'amincissement maximal de la croûte. Les effets de la subsidence tectonique et thermique sont figurés sous le schéma par des flèches descendantes ou ascendantes.

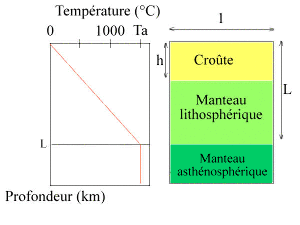
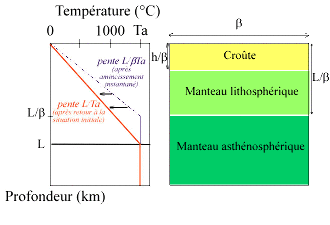
Le modèle de Mc Kenzie est un modèle vertical à deux dimensions. L'asthénosphère est supposée à une température constante T_a. La lithosphère est définie comme la couche située entre la surface de température T = 0°C et l'isotherme T = T_a. Le gradient thermique dans la lithosphère est supposé constant, c'est-à-dire : T(z) = zT_a / L où z est la profondeur (figure 9).

Figure 9. Modèle de McKenzie, situation initiale

Les densités de la croûte et du manteau sont données par : ρc(z) = ρc₀[1 - αT(z)] et ρm(z) = ρm₀[1 - αT(z)] où α est le coefficient d'expansion thermique ; ρc₀ et ρm₀ sont les masses volumiques de la croûte et du manteau à 0°C. La masse volumique de l'asthénosphère est donnée par : ρa = ρm₀(1 - αT_a).

Figure 10. Modèle de McKenzie, amincissement lithosphérique homogène instantané

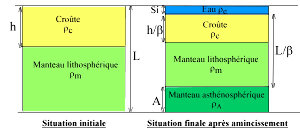
La lithosphère s'amincit instantanément d'un facteur β. Chaque couche remonte vers la surface, sans changer de température (figure 10 et 11). Ceci implique que :

Après étirement, la lithosphère est plus chaude qu'avant étirement. Elle va ensuite progressivement se refroidir jusqu'à ce que le gradient géothermique retrouve sa valeur initiale (figure 11).

Figure 11. Modèle de McKenzie, retour vers le gradient géothermique initial