Application du principe d'isostasie aux plateaux éthiopiens

Dans une conférence, Gravimétrie et isostasie, deux clés essentielles pour comprendre le fonctionnement de la Terre (diapositive 54 du diaporama, vers 1h06min35s de la première vidéo), il est montré qu'un calcul simple permet de déterminer l'altitude d'une dorsale océanique par rapport aux plaines abyssales environnantes. On trouve que x = h/45, avec x la différence d'altitude induite et h l'épaisseur du manteau lithosphérique (ou celle de l'amincissement de ce niveau, ce qui revient au même dans le cas d'une dorsale). On a alors une dorsale qui surplombe les plaines abyssales d'environ 2,07 km avec les valeurs moyennes proposées.

Sauf erreur de ma part, si on applique ce calcul au cas d'un rifting actif - afin de calculer l'altitude du bombement thermique - alors la principale différence réside dans l'absence d'eau, et on obtient alors x = h/65 (comme indiqué dans la même diapositive).

Le problème c'est qu'avec un manteau lithosphérique d'une centaine de kilomètre on trouve un bombement d'environ 1,5 km, alors que les plateaux éthiopiens et somaliens culminent à 2,5 km d'altitude, soit au moins 2  au-dessus des terrains “avoisinnants” culminant à 400-500 m. J'ai volontairement simplifié en ne tenant pas compte de la subsidence tectonique responsable de la vallée du rift. Ou ai-je commis une erreur ?

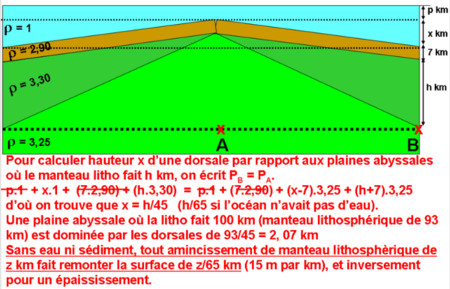
Source - © 2012 in P.Thomas

Figure 1. Calcul simple (simpliste) d'isostasie

Dans ce calcul permettant d'obtenir rapidement un ordre de grandeur, on remarque que la hauteur et la densité de la croute n'ont pas d'influence sur le calcul dans le cas d'une croute (ici océanique mais qui pourrait être continentale) d'épaisseur constante. Parmi toutes les variables, seuls l'amincissement du manteau lithosphérique et les densités mantelliques entrent finalement en compte (remplacement d'une hauteur de manteau dense par une hauteur plus importante de manteau moins dense).

Page 54 du diaporama de la conférence Gravimétrie et isostasie, deux clés essentielles pour comprendre le fonctionnement de la Terre.

Il n'y a pas que l'absence d'eau comme différence lorsqu'on s'intéresse à la hauteur des plateaux éthiopiens et non plus au cas théorique des dorsales océaniques.

Tout d'abord, il y a l'épaisseur de la lithosphère, et plus précisément du manteau lithosphérique. Le manteau lithosphérique est plus épais sous les vieux cratons, ce qui est le cas de l'Afrique. Si on ne met pas d'eau, sans variation d'épaisseur de la croute, et avec le calcul simplissime proposé, toute variation “e” d'épaisseur du manteau lithosphérique entraine une variation d'altitude de “e/65”. Si vous considérez que l'altitude moyenne du craton africain est de 500 m, l'Éthiopie est alors 2 km plus haut. Il “suffit” donc d'un écart de 65 × 2 = 130 km entre l'épaisseur du manteau lithosphérique sous le craton stable et sous le rift. Or, il se trouve que sous l'Afrique du Sud, l'isotherme 1300°C se situe vers 175 km, soit un manteau lithosphérique de 130 à 140 km d'épaisseur. Ce qui pourrait expliquer l'altitude observée dans ce cadre très théorique avec “disparition” complète du manteau lithosphérique sous le rift Est-africain.

Autre différence, la température du manteau sous-lithosphérique joue aussi un rôle. Le rifting est actif sous l'Est africain, c'est-à-dire qu'on est sous un point chaud. Si on suppose que le manteau sous ce point chaud est 100°C plus chaud que le manteau situé à la même profondeur mais à côté, sur 1000 km de profondeur, et qu'on prend le coefficient de dilatation thermique des péridotites mesuré en laboratoire qui est de l'ordre de 2,5.10⁻⁵ K⁻¹, alors la dilatation verticale induite est de l'ordre de 2,5 km (100 × 1000 × 2,5.10⁻⁵). Un calcul simple de comparaison de pression est ici difficile car il faudrait connaitre la variation de densité du manteau sous le craton stable et dans le panache plus chaud sur 1000 km de profondeur, d'où un calcul d'ordre de grandeur proposé utilisant la dilatation thermique supposée constante et isotrope sur les 1000 km considérés.

Bien sûr, les calculs présentés ne permettent d'obtenir que des ordres de grandeur (pas si mauvais que ça). On peut noter 3 “raffinements” possibles.

Le calcul d'isostasie prend en compte l'amincissement du manteau lithosphérique à l'aplomb du point considéré, cet amincissement “h” ne correspond à l'épaisseur initiale de ce manteau, estimée en prenant l'épaisseur “à côté”, sous craton stable, que si on considère une “disparition” complète. Le bombement sera moindre si le manteau lithosphérique initial n'a pas complètement “disparu” et/ou si une partie du manteau asthénosphérique a refroidi et a retrouvé un densité lithosphérique (réajustement thermique).

Le calcul de dilatation thermique prend ici des valeurs de hauteur de manteau “réchauffé” et d'écart de température “moyenne” correspondant à des points chauds “classiques”, pas forcément exactement adaptées au cas éthiopien. De plus, le coefficient de dilatation thermique dépend de la pression et la valeur donnée correspond plutôt à une valeur haute si on veut l'appliquer à une colonne de 1000 km. Les valeurs utilisées permettent cependant d'estimer l'effet “moyen” d'un point chaud “moyen” en première approximation.

Enfin, dans le cas d'un rift continental, on devrait prendre en compte la variation d'épaisseur de la croute. En effet, dans le calcul d'isostasie effectué, le bombement calculé correspond au remplacement d'une hauteur de manteau lithosphérique par une hauteur supérieure de manteau asthénosphérique moins dense. Si on prend en compte un amincissement crustal, un amincissement donné est remplacé par une hauteur moindre de matériau mantellique plus dense. Ainsi, le bombement lié à l'amincissement du manteau lithosphérique peut en partie être contrebalancé par un affaissement lié à l'amincissement crustal. Un amincissement crustal de l'ordre de 10 à 15 % peut alors suffire à expliquer un bombement moins élevé de 500 m par rapport à un calcul à épaisseur de croute continentale constante. Si on revient au rift Est-africain, l'amincissement crustal est bien supérieur à 10-15 % et explique les basses altitudes, parfois sous le niveau de la mer, à l'“axe” du rift. Mais latéralement, des épanchements importants de basaltes ainsi que des placages sous-crustaux peuvent au contraire épaissir la croute (croute continentale initiale augmentée par le dessus et le dessous de basaltes), épaississement qui entraine alors une surrection. Dans ce cadre, un épaississement crustal de l'ordre de 2 à 3 km seulement expliquerait une surrection latérale supplémentaire de l'ordre de 500 m.