Les mesures gravimétriques de Bouguer au Pérou

Dans cet article, nous abordons une belle utilisation historique du pendule : la découverte et l'explication des variations de la pesanteur avec l'altitude par Pierre Bouguer (1698-1758). Nous étudions également comment Bouguer mesure la déviation de la verticale par l'attraction des montagnes. Ces travaux sont fondamentaux et permettent à la gravimétrie de franchir une nouvelle étape. Trois points peuvent être retenus : la précision apportée dans les mesures et dans leurs corrections, la confirmation par de nouvelles « observations tests » de la supériorité du système de Newton sur celui de Huygens, et l'application de la gravimétrie à la connaissance de la constitution physique de la Terre grâce à l'interprétation de mesures locales. Ce dernier aspect est le plus novateur et contribue à redonner une impulsion à la gravimétrie en lui ouvrant un nouvel horizon : la connaissance des profondeurs du globe.

Paris, Musée du Louvre.

Source - © RMN-Grand-Palais

Figure 1. Portrait de Pierre Bouguer de l'Académie de Sciences

Tableau de Jean-Baptiste Perronneau, 1753.

C'est au cours de l'expédition géodésique au Pérou (*), entre 1735 et 1744, que Pierre Bouguer réalise ses mesures pendulaires et ses mesures de la déviation de la verticale consignées dans son livre La Figure de la Terre, paru en 1749 [1]. Bouguer a été envoyé au Pérou par l'Académie des Sciences, en compagnie de Godin, La Condamine et Jussieu pour réaliser des mesures astronomiques et des mesures géodésiques. Le but est de trouver quelle est la forme exacte de la Terre : sphérique, aplatie aux pôles ou allongée selon l'axe de rotation. Ce voyage, qui dure 9 ans, est épique. Les académiciens subissent un tremblement de terre, une épidémie, une révolte de la population locale et un climat montagneux parfois rude. Coupés de la France, ils doivent également subvenir à leurs besoins sur place, et pour ce faire l'un d'entre eux développe un trafic d'or ! Les personnes de l'expédition se divisent, certaines sont mortes, d'autres ont sombré dans la folie [2]... Ce voyage est cependant d'une très grande richesse d'un point de vue scientifique : mesure d'un degré du méridien, mesure de la vitesse du son, mesure de la réfraction atmosphérique, détermination des altitudes grâce au baromètre et, nous allons le voir, mesure de la diminution de la pesanteur avec l'altitude ainsi que mesure de la déviation de la verticale par l'attraction des montagnes.

Source - © 1749 Pierre Bouguer [1]

Figure 2. La Cordillère, coupe et vue de Quito

Source web : ECHO, Max Planck Institut für Wissenschaftsgeschichte ("page" 252)

Bouguer est un observateur précis, méticuleux, soucieux du sens de ses mesures et du contexte dans lequel elles sont effectuées. Par exemple, pour ses mesures de pesanteur, il détaille deux corrections à appliquer aux mesures. La première est classique, il s'agit d'une correction de température pour tenir compte de la dilatation des matériaux du pendule. La deuxième est originale, c'est une correction de pression, pour tenir compte, non de la résistance de l'air qui a un effet négligeable, mais de sa densité qui, par la force d'Archimède, diminue la densité du poids du pendule. Bouguer insiste sur la pertinence et la nouveauté de cette correction. Elle montre son désir d'exactitude et la maîtrise de ses observations. Elle révèle un nouvel état d'esprit, qui va se poursuivre tout au long du XVIII^ème siècle. Les savants changent leur approche des mesures et cela va transformer la physique elle-même ! Ils prennent un soin extrême dans la construction de leurs instruments, répètent leurs mesures jusqu'à les rendre les plus précises possible. Ils apprennent à éviter le maximum de perturbations et lorsque cela n'est pas possible, ils apprennent à calculer des corrections. Cet accroissement de la qualité des mesures constitue un développement considérable des sciences expérimentales et Bouguer est l'un des principaux contributeurs.

Au cours de son séjour au Pérou, Bouguer a effectué une série de mesures pendulaires, à trois altitudes différentes : au niveau de la mer, à Quito et à Pichincha (tableau ci-dessus). Si la gravité suit la loi de Newton en 1/r², la variation relative de la pesanteur (la variation de la force centrifuge avec l’altitude étant négligeable) est en « raison doublée des distances », soit Δg/g=−2h/R (où h est l’altitude et R le rayon de la Terre). En effet, si g est la pesanteur au niveau de la mer et g' la pesanteur à l'altitude h, la variation de pesanteur s'écrit (nous négligeons ici l'effet de la rotation journalière) :

Bouguer remarque que la diminution de la pesanteur déduite des mesures pendulaires réalisées à Quito et à Pichincha est bien réelle, importante, mais qu'elle ne suit pas exactement ce rapport, ce qui pose de sérieuses questions : « Mais pourquoi nos expériences nous donnent-elles donc constamment un rapport qui n'est pas tout à fait conforme ? Faut-il attribuer à quelque erreur de notre part cette différence ; ou serait-il vrai que dans le voisinage des grosses masses comme la Terre, la loi dont il s'agit ne fut observée que d'une manière imparfaite ? » ([1], p.358). Comment expliquer le désaccord entre les observations et la diminution théorique de la gravité[1]? Faut-il supposer que la loi est perturbée dans le voisinage de la Terre, comme l'a suggéré Huygens, qui écrivait en 1690 : « Je dis qu'il ne serait par étrange si la pesanteur, près de la surface de la Terre, ne suivait pas précisément, ainsi que dans les régions plus élevées, la diminution que font les différentes distances du centre ; parce qu'il se peut que le mouvement de la matière qui cause la pesanteur, soit (…) altéré dans la proximité de la Terre, comme il l'est apparemment au-dedans »[3]. Faut-il remettre en cause la loi de Newton ?

Le tour de force de Bouguer est de montrer que ses observations, loin de remettre en cause l'attraction newtonienne, en apportent au contraire une nouvelle confirmation. Bouguer remarque que lorsqu'on détermine la diminution de la gravité en fonction de l'éloignement au centre de la Terre, on ne tient pas compte des masses situées entre le niveau de la mer et l'altitude des mesures. Or ces masses possèdent une capacité d'attraction qu'il faut considérer. Il expose : « Il y a donc deux diverses attentions à avoir, lorsqu'il s'agit des expériences que j'ai rapportées sur le pendule. Ces expériences ont été faites à une plus grande distance de la Terre : par conséquent la pesanteur a dû se trouver un peu plus petite. Mais d'un autre côté, le groupe de montagnes sur lequel est placé Quito et sur lequel est élevé Pichincha et tous les autres sommets auxquels il sert de plinthe, doit produire à peu près le même effet que si la Terre en cet endroit, était plus grosse ou d'un plus grand rayon. La pesanteur a donc dû augmenter » ([1], p.359). Bouguer comprend que les masses représentées par les montagnes compensent en partie le plus grand éloignement au centre de la Terre. En termes modernes, nous dirions que Bouguer introduit deux corrections dans les mesures de l'intensité de la pesanteur : la correction à l'air libre (éloignement au centre de la Terre) et la correction de plateau (attraction des masses situées entre le niveau de la mer et le point de mesure). La première était déjà discutée avant lui, la deuxième est entièrement originale.

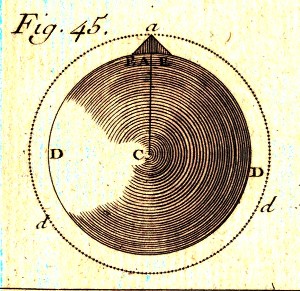
Bouguer cherche à quantifier cette deuxième correction. Il s’appuie sur sa figure 45 (cf. ci-dessous) où ADD représentait la Terre de densité ρ, Aa l’altitude h de Quito situé en a, et l’intervalle entre les surfaces ADD et add une couche sphérique de densité δ. En modélisant la Cordillère comme un prisme aEE (« la forme d’un toit de maison ») de longueur indéfinie, puis en affirmant que la base de la Cordillère est très large devant sa hauteur, il trouve que l'attraction d'une montagne vaut, à son sommet, $2\mathrm{\pi }G\delta h$. Pour retrouver ce résultat, nous modéliserions aujourd’hui la montagne comme un cône de hauteur h et d’angle au sommet α. L’attraction au sommet d'un cône serait donc $2\mathrm{\pi }G\delta (1-\cos \frac{\alpha }{2})h$. En supposant que la base du cône est très grande devant sa hauteur, l’angle α tendant vers 180°, nous obtiendrions alors que l’attraction au sommet vaut $2\mathrm{\pi }G\delta h$.

Avec ce résultat, Bouguer peut montrer que la variation relative de la pesanteur en a (au sommet de la montagne) vaut $\frac{\Delta g}{g}=(-2+\frac{3}{2}\frac{\delta }{\rho })\frac{h}{R}$. En effet, soit g' la pesanteur à l'altitude h (sans tenir compte de la montagne). La pesanteur au sommet de la montagne d'altitude h est $\mathrm{g\text{'}}+2\mathrm{\pi }G\delta h$. La variation de pesanteur devient :

La variation relative de la pesanteur est donc :

Source - © 1749 Pierre Bouguer [1]

Figure 3. Figure de Bouguer illustrant son calcul de « correction de plateau »

Source web : ECHO, Max Planck Institut für Wissenschaftsgeschichte ("page" 559)

Bouguer se sert de ce résultat pour montrer que la diminution de la pesanteur avec l'altitude dépend de certaines circonstances. Si, par exemple, la densité de la montagne était les 4/3 de la densité moyenne de la Terre, la pesanteur à Quito serait égale à celle qu'on éprouvait au niveau de la mer. Si la densité de la montagne était encore plus forte, la pesanteur pourrait même augmenter avec l'altitude ! Le raccourcissement du pendule avec l'altitude est cependant indéniable, ce qui permet à Bouguer de conclure que la densité superficielle des montagnes est plus petite que la densité moyenne du globe. En utilisant ses observations pour Quito, $\frac{\Delta g}{g}=\frac{-1}{1333}$ et $\frac{h}{R}=\frac{1}{2237}$, Bouguer calcule que $\frac{\delta }{\rho }=\frac{2}{3}(2+\frac{R}{h}\frac{\Delta g}{g})=\mathrm{0,21}$.

Les variations de l'intensité de la pesanteur avec l'altitude peuvent donc s'interpréter dans le cadre de la conception newtonienne de la gravitation : nul n'est besoin de modifier la loi dans la proximité de la Terre, il suffit de considérer l'attraction des montagnes elles-mêmes (modélisées comme des plateaux). Ce qui apparaissait comme une difficulté sérieuse se révèle donc au contraire comme un argument supplémentaire en faveur du système de Newton !

La prise en compte de l'attraction des masses montagneuses est en outre extrêmement féconde puisqu'elle aboutit à l'estimation du rapport entre la densité superficielle et la densité moyenne de la Terre, rapport qui se trouve inférieur au quart (0,21). Bouguer en tire la conclusion suivante : « Ainsi il faut convenir que la Terre est beaucoup plus compacte en bas qu'en haut, et dans l'intérieur qu'à la surface. Car le sol de Quito est comme celui de tous les autres pays : il est mêlé de terre, de pierres et chargé tout au plus de quelques parties métalliques. C'est à une certaine profondeur que doit se faire le changement, et on ne peut pas douter qu'il ne soit très considérable. Il parait aussi, si nous osons porter quelque jugement, sur un sujet couvert pour nous d'une si grande obscurité, qu'il était beaucoup plus convenable d'augmenter la solidité de toutes les Planètes, afin de leur donner plus de force pour continuer leur mouvement dans les espaces célestes. Ces Physiciens qui supposaient au milieu de la Terre un grand vide et qui voulaient que nous marchassions sur une espèce de croûte extrêmement mince n'y pensaient pas assez. On peut faire à peu près la même objection contre la grande masse des eaux intérieures de Woodward »[1], p.363-364). Bouguer, non seulement affermit le système de Newton, mais montre en outre comment la gravimétrie apporte des connaissances sur la constitution intérieure de la Terre et permet de conclure à la forte densité des profondeurs. Grâce à ses mesures pendulaires, il peut ainsi réfuter les modèles de Terre creuse ou les modèles de Terre contenant un noyau aqueux.

On sait aujourd'hui que le rapport δ/ρ est proche de 0,5 et est donc assez éloigné de la valeur trouvée par Bouguer. L'écart ne provient pas d'une erreur dans les mesures de Bouguer mais s'explique, d'une part, parce que Bouguer ne tient pas compte de ce qu'on appelle aujourd'hui la « correction topographique » (les montagnes et les vallées à proximité du point de mesure diminuent légèrement la pesanteur par leur attraction ou leur déficit d'attraction) et surtout, d'autre part, parce que sous les montagnes se trouvent des anomalies de masse (les « racines » des montagnes) qui causent un déficit d'attraction important, anomalies à prendre en compte pour les Andes (mesures de pesanteur à Quito par rapport aux mesures en bordure du Pacifique), pas pour le Chimborazo qui n'est qu'un épiphénomène à l'échelle de la lithosphère andine. Pour appliquer la méthode de Bouguer, il faudrait d'abord corriger les mesures pendulaires de l'effet de ces anomalies internes de masse. C'est bien sûr le contraire qui est effectué, on se sert des mesures de pesanteur pour déterminer les anomalies internes et c'est ainsi que fut découverte la compensation isostatique des reliefs. L'idée de Bouguer de déterminer le rapport δ/ρ grâce à des mesures pendulaires était donc vouée à l'échec. Elle n'en reste pas moins remarquable.

Dans son ouvrage de 1749, Bouguer insère un Mémoire sur les attractions et sur la manière d'observer si les montagnes en sont capables écrit en 1738. La motivation de ce mémoire est de vérifier le fait brut de l'attraction mutuelle et de s'assurer que tous les corps y sont sujets, en observant la déviation de la verticale au voisinage des reliefs. Bouguer a été profondément marqué par l'immensité des montagnes péruviennes et de là, selon lui, son idée : si les corps agissent en distance, à proportion de leur matière, ces grandes masses doivent nécessairement produire un effet marqué, et détourner la direction de la pesanteur. En estimant que la montagne Chimborazo a un volume de 1/7.400.000.000 fois celui du globe, que sa densité est égale à celle de la Terre, et en remarquant que la mesure est effectuée à une distance 1900 fois plus proche du centre de gravité de la montagne que du centre de gravité de la Terre, il calcule grossièrement que l'attraction de la montagne valait 1/2000 fois l'attraction de la Terre, et donc que la déviation de la verticale doit être de 1'43". En effet, en supposant que la montagne agit comme un corps ponctuel et qu'elle ait même densité que la Terre, le rapport de l'attraction de la montagne sur l'attraction de la Terre est égal à : $\frac{M_{\text{m}}}{M_{\text{T}}}{\left(\frac{R_{\text{T}}}{d}\right)}^2=\frac{{1900}^2}{7400000000}\approx \frac{1}{2000}$. L'angle de déviation est donc tan⁻¹(1/2000)=1'43''. L’effet est significatif et doit pouvoir être mis en évidence.

Comme précédemment, Bouguer imagine donc une nouvelle « observation test », cette fois la déviation de la verticale, qui doit permettre de valider ou d'infirmer le système de Newton. L'idée de Bouguer est simple dans son principe, mais délicate dans sa mise en œuvre. Car comment reconnaître la déviation de la verticale ? Le fil à plomb, la chute des corps, la perpendiculaire à la surface de niveau d'un fluide, ne donnent accès qu'à une seule direction, celle de la verticale « réelle », perturbée par la montagne. La direction de la verticale qui existerait en l'absence de montagne, ne peut pas être connue. Il n'y a donc pas de terme de comparaison. Bouguer cherche ainsi à développer une méthode de mesure appropriée, indirecte, capable de contourner la difficulté. Il expose deux méthodes. Pour la première, il explique : « Il n'y aura qu'à se mettre au Nord ou au Sud d'une montagne,et à la moindre distance qu'il se pourra de son centre de gravité, et y observer la latitude. (…) On se transportera ensuite sur la même ligne Est et Ouest, jusqu'à une assez grande distance, pour qu'il n'y ait plus d'action à craindre : et si on observe la latitude dans ce second endroit, avec le même soin et par les mêmes moyens que dans le premier, il est évident que toute la différence qu'on apercevra sera due à l'attraction. Pour se mettre précisément dans la seconde observation à l'Est ou à l'Ouest du lieu de la première, il faudra observer l’azimut du Soleil à son lever ou à son coucher, en comparant cet Astre à quelque point remarquable de l'horizon » ([1], p.370). Pour la deuxième méthode (figure ci-après), Bouguer explique qu'il faut déterminer la latitude au Sud et au Nord de la montagne. Ces valeurs des latitudes sont perturbées par l'attraction de la montagne et comme la verticale s'incline au Nord et au Sud dans des directions opposées, l'effet de la déviation se trouve doublé. En mesurant ensuite la distance entre les deux stations par triangulation géodésique et en supposant connue la figure géométrique de la Terre, on pouvait connaître la différence de latitude géodésique entre les deux stations. L'écart entre la différence des latitudes astronomiques (dépendant de la verticale "locale") et la différence des latitudes géodésiques (exercice de géométrie sphérique) représente la somme des déviations exercées par la montagne. Les deux méthodes ainsi exposées par Bouguer sont lumineuses.

Source - © 2013 Vincent Deparis / Pierre Thomas

Figure 4. Effet de l'attraction d'une montagne, ici le volcan Chimborazo, sur la direction de la verticale

Aux stations A et B, les verticales sont données par les lignes AM et BM', alors qu'en l'absence de montagne, elles seraient données par AO et BO'.

C'est la première méthode qu'il met en œuvre au Chimborazo. Aidé par La Condamine, il réalise comme à son habitude ses mesures avec grand soin. Son compte-rendu précis permet de suivre dans le détail les différentes étapes des observations. Il arrive au résultat suivant : l'attraction du Chimborazo provoque une déviation de la verticale de 7"1/2 ([1], p.389). La déviation est donc près de quatorze fois plus petite que l'estimation grossière qu'il a effectuée ! La déception de Bouguer est grande : « Il faut bien avouer que cet effet est bien différent de celui auquel nous pouvions nous attendre. Mais nous savons si peu quelle est la densité de la Terre, et d'un autre côté celle des montagnes peut être si différente de celle que nous leur attribuons, qu'il n'y a lieu de s'étonner de rien. Nous avons remarqué aussi sur Chimborazo quelques pierres calcinées, et depuis que nous en sommes descendus on m'a dit et on l'a aussi confirmé à M. de la Condamine, que c'était une tradition assez établie, que cette montagne avait été Volcan » ([1], p.389). Il ajoute en 1749 : « Il parait assez qu'on peut dire en se refermant dans le fait simple, que les montagnes agissent en distance, mais que leur action est bien moins considérable que le promet la grandeur de leur volume. Chimborazo peut contenir quelques concavités, mais cependant on ne peut pas supposer qu'il soit creux comme Cotopaxi. Cette dernière montagne ouverte par le haut, forme comme une immense chaudière, dont le pourtour doit avoir très-peu d'épaisseur. (…) Ce ne doit pas être la même chose à l'égard de Chimborazo. (…) C'est beaucoup que de supposer son volume diminué de moitié par les concavités qu'elle peut avoir, et il s'ensuivra que malgré ses bancs de rochers vifs, elle sera encore six à sept fois moins compacte que notre Globe. Après tout, il n'y a rien en cela qui répugne. Il suffisait que les matières métalliques dont nous avons l'usage, restassent ensevelies pour nous quelques centaines de toises plus bas dans les entrailles de la Terre, pour que nous n'en eussions aucune connaissance » ([1], p.391).

Le principal est fait : démontrer l'attraction en distance des montagnes. Mais la petitesse de la déviation reste déconcertante, et Bouguer ne peut l'expliquer qu'en postulant que la densité de la montagne est très faible devant la densité du globe, dans un rapport de six à sept. Un auteur moderne (Jean Goguel) a eu l'occasion, grâce aux cartes topographiques de la région de Chimborazo, de calculer par une méthode moderne les déviations de la verticale que Bouguer a essayé de mesurer ([4] et [5]). Il trouve que le Chimborazo provoque une déviation de la verticale de 11". En considérant une incertitude probable de 4" sur les mesures de Bouguer, on voit que celles-ci, qui donnaient un résultat de 7''1/2, étaient bonnes. D'où provient l'écart entre les observations et le calcul de Bouguer ? Aujourd'hui, nous savons que la densité des roches superficielles est effectivement plus faible que la densité moyenne de la Terre, mais seulement dans un rapport de 2. Ceci réduit déjà de moitié le résultat de son calcul initial. Comment expliquer le reste de la différence ? D'abord, Bouguer confond l'attraction de la montagne avec l'attraction de sa masse rassemblée au centre de gravité, ce qui n'est vrai que dans le cas d'une sphère. D'autant plus que pour effectuer sa première mesure, il ne se place pas au pied de la montagne mais à mi-hauteur du flanc et donc qu'une partie de la montagne dévie la verticale dans le sens inverse où il veut l'observer. Cette erreur dans le calcul de l'attraction surestime largement l'effet de la montagne et s'il en avait tenu compte, l'effet de surprise devant le résultat trouvé aurait été grandement atténué. Mais surtout, Bouguer ne tient pas compte (comment le pourrait-il ?) des racines des montagnes qui réduisent fortement la déviation de la verticale. C'est d'ailleurs en renouvelant les mesures de Bouguer sur les variations de l'intensité et de la direction de la pesanteur aux pieds des chaînes de montagnes que Pratt et Airy aboutiront au XIX^ème siècle à la théorie de l'isostasie.

Avec Bouguer, les mesures pendulaires et gravimétriques prennent une nouvelle importance. Il trouve de nouvelles « observations tests » pour vérifier la pertinence du système newtonien. Il sait les mettre en œuvre en développant des procédés astucieux pour contourner les difficultés insurmontables et les interpréter en élaborant de nouveaux concepts adéquats. Lorsqu'on sait que tout ceci a été réalisé dans la solitude de sa mission au Pérou, on ne peut que souligner son ingéniosité et sa persévérance. Ses travaux les plus novateurs concernaient la reconnaissance de l'attraction propre des montagnes. Ils donnent une nouvelle dimension à la gravimétrie en permettant une connaissance du sous-sol et plus particulièrement de la répartition des densités. En mettant en évidence que des effets locaux (altitude, topographie et il faudrait ajouter anomalies internes de masse) affectent les mesures de l'intensité et de la direction de la pesanteur, Bouguer montre qu'avant de pouvoir être utilisées et interprétées dans un cadre plus général (celui des figures d'équilibre), elles doivent être préalablement corrigées.