Article | 21/06/2010
Gravitation, pesanteur
21/06/2010
Résumé
Définition de la force gravitationnelle, du potentiel et du champ de pesanteur.
Table des matières
Interaction gravitationnelle, champ de gravitation, pesanteur
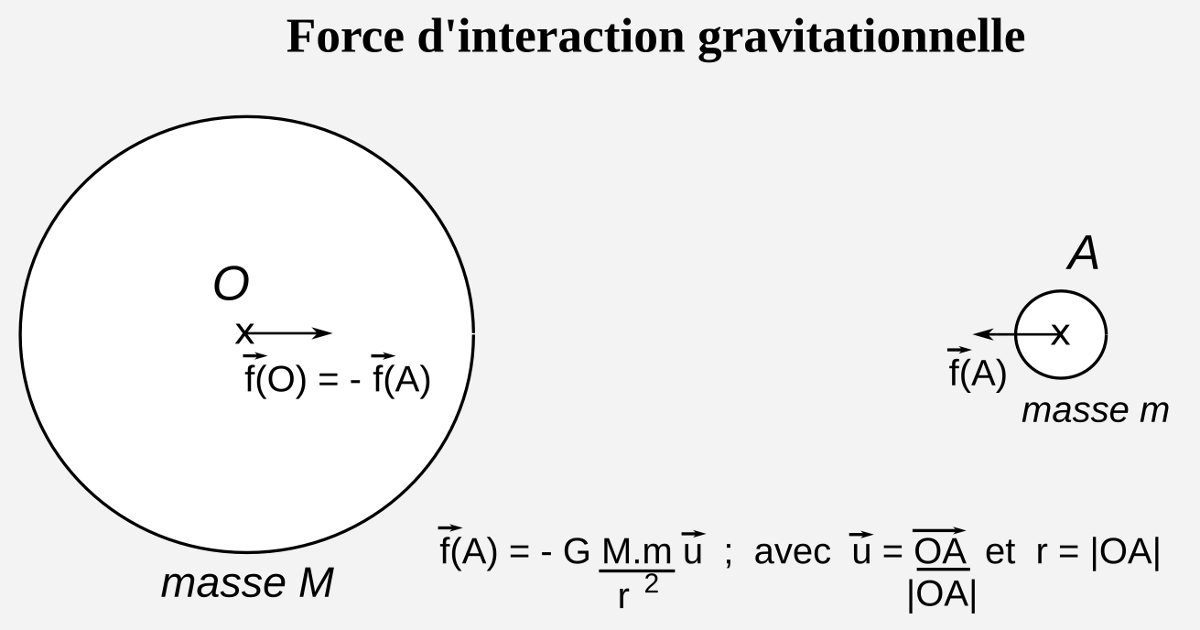
La base : deux corps massiques exercent l'un sur l'autre une force d'attraction appelée interaction gravitationnelle. Pour deux corps ponctuels ou sphériques, cette force croît en fonction de la masse de chaque corps et diminue selon le carré de la distance entre ces deux corps.
Soit un corps ponctuel de masse m placé au point A, et un corps ponctuel ou sphérique (de densité homogène ou à couches homogènes concentriques) de masse M distant de R=OA. La force d'attraction gravitationnelle exercée sur la masse m est donnée par l'équation suivante (équation 1).
La force gravitationnelle exercée sur une masse m ne dépend que de sa position par rapport à O. On dit que la masse M génère un champ gravitationnel ou champ de gravitation que l'on peut mettre en évidence par la force exercée sur une masse placée en A.
Dans le référentiel terrestre tournant, à la force de gravitation s'ajoute la force centrifuge liée à la rotation de la Terre autour de son axe. La somme de la force de gravitation et de la force centrifuge est appelée force de pesanteur.
De même qu'on a introduit la notion de champ gravitationnel, on définit le champ de pesanteur (ou pesanteur) γ (gamma) associé à la force de pesanteur, tel que f = m γ.
Champ et énergie potentielle, ligne équipotentielle
Énergie potentielle
À tout point A de l'espace est associé une énergie potentielle notée Ep(A). La force de pesanteur dérive de cette énergie potentielle. Cela signifie que la force de pesanteur au point A dépend des variations de cette énergie autour de ce point (la dérivée en 1D ou différentielle totale en 2-3D) (équation 2).
On définit le potentiel de pesanteur W, tel que Ep(A) = m.W(A) (une autre convention existe, Ep(A) = -m.W(A)... attention à la convention choisie dans un ouvrage). On peut alors écrire, équation 3, :
On appelle surface équipotentielle, ou équipotentielle, une surface sur laquelle le potentiel de pesanteur W est constant. Une propriété importante est que la pesanteur γ est perpendiculaire en tout point aux équipotentielles de pesanteur.
Couramment, en physique (au lycée) on distingue deux types de situations : études de trajectoire à proximité du sol ou études de satellites (naturels ou artificiels).
Pour l'étude de trajectoires à proximité du sol, pour de faibles variations d'altitude z (avec z=0 à la surface du sol), on considère un champ de pesanteur uniforme : g(z) = g(0) = g et l'on fixe comme référence Ep(0) = 0. L'énergie potentielle est alors donnée par : Ep(z) = mgz. Cette expression est utilisée dans les problèmes de "saut à ski", de trajectoire de projectile, de mouvement d'une bille sur une surface, avec ou sans vitesse initiale, avec ou sans frottements.
Pour l'étude des satellites, avec des variations d'altitude importantes, on considère la seule force gravitationnelle exercée par la Terre et on fixe une énergie potentielle nulle à l'infini, Ep(∞) = 0. L'énergie potentielle est alors donnée par : Ep(r) =-m.GM/r, avec M la masse de la Terre. Cette expression est utilisée dans les problèmes de vitesse de libération, de mise en orbite de satellites...
Pour l'étude de la Terre réelle, l'expression de l'énergie potentielle est Ep(r, φ, λ) = - mGM/R + ε(r, φ, λ), avec ε une perturbation qui dépend de la distance r, de la longitude φ et de la latitude λ.
Une analogie simple : gravimétrie / topographie
Une analogie simple à la relation pesanteur / potentiel de pesanteur / équipotentielle est la relation pente / altitude / courbe de niveau en topographie.
Le champ est d'autant plus fort que, pour un déplacement élémentaire dans sa direction, la variation d'énergie potentielle est importante. De même, la pente est d'autant plus forte que, pour un déplacement dans le sens de la pente, la variation d'altitude est importante. On voit donc que plus les équipotentielles ou les courbes de niveau sont rapprochées plus le champ ou la pente sont forts.
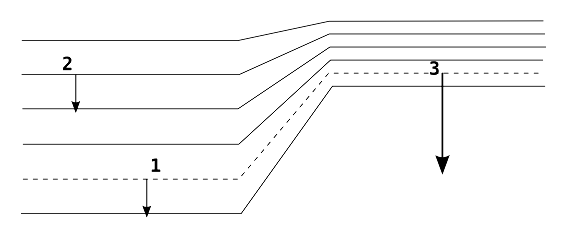
Figure 2. Illustration de l'analogie pente - champ, courbes de niveau - équipotentielles Considérons une carte topographique. Les (lignes de plus grandes) pentes sont perpendiculaires aux courbes de niveau et la pente est plus forte là où les courbes sont les plus rapprochées (point 3). Notons qu'aux points 1 et 2 la pente est la même pour des altitudes différentes, alors que les points 1 et 3 sont à la même altitude (même courbe de niveau) avec des pentes différentes. Si cette figure représente cette fois des équipotentielles de pesanteur. La pesanteur est plus forte là où les équipotentielles sont plus rapprochées (point 3). Notons qu'aux points 1 et 2 la pesanteur est la même pour des potentiels différents, alors que les points 1 et 3 sont au même potentiel (même ligne équipotentielle) avec des pesanteurs différentes. |
La différence d'information apportée par les cartes d'altitudes et de pentes est illustrée ci-dessous sur les alentours du massif de la Chartreuse. Des images, cartes, ..., sont aussi disponibles via le Géoportail et sur Google earth.
Les amateurs de neige choisiront les points hauts (Sud-Est de la carte), alors que les amateurs d'escalade auront déjà de quoi faire même à basse altitude dans le massif de la Chartreuse.
Remarquons que les barres calcaires qui façonnent le paysage de la Chartreuse ressortent bien, en rouge, sur la carte des pentes.
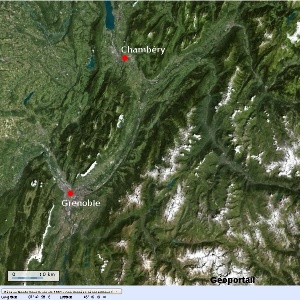
Figure 3. Les environs de Grenoble-Chambéry, vallée de l'Isère Vue englobant les images suivantes. | |
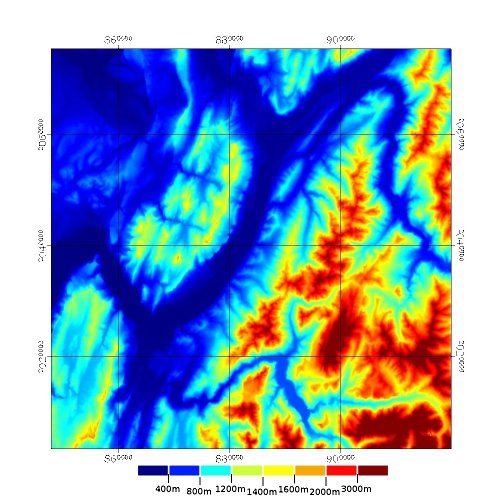
Figure 4. Les alentours du massif de la Chartreuse : carte des altitudes On reconnaît la vallée de l'Isère et sa clue de Grenoble. Pour le ski, la neige d'altitude est à chercher à l'Est et au Sud (Grandes Rousses et Oisans). Carte disponible sous forme de carte topo avec courbes de niveau. | Figure 5. Les alentours du massif de la Chartreuse : carte des pentes On reconnaît la vallée de l'Isère et sa clue de Grenoble. Pour l'escalade, même à (relativement) basse altitude, de bonnes "falaises" (en rouge) sont présentes dans la Chartreuse. Carte disponible sous forme de carte avec courbes de pentes. |
En topographie, on donne une valeur de l'altitude par rapport à une référence : cette référence est le niveau moyen des océans dont l'altitude vaut donc 0 (zéro).
Dans un champ de pesanteur, la surface limite libre et à l'équilibre entre deux fluides est une équipotentielle. La limite entre l'eau des océans et l'air de l'atmosphère, limite entre deux fluides, supposés au repos, est l'équipotentielle de pesanteur de référence, appelée géoïde.