Article | 23/06/2010
Gravimétrie et géodésie : principes, applications
23/06/2010
Résumé
Ellipsoïde et géoïde, gravimétrie, corrections et anomalies : surface et profondeur de la Terre.
Table des matières
Mesure de la pesanteur : les gravimètres
La gravimétrie est la mesure et l'étude la pesanteur (ou champ de pesanteur, noté γ) à la surface de la Terre, en direction et en norme.
L'unité de mesure est le m.s-2 (équivalent ou N.kg-1). Une autre unité est utilisée, le Gal (1Gal = 1cm.s-2 = 10-2m.s-2) et son millième, le mGal (1 mGal = 10-5 m.s-2).
La valeur "moyenne" de la pesanteur à la surface de la Terre vers 45° de latitude est g = 9,81 m.s-2= 981 Gal.
Source - © 2010 EOST, Strasbourg
Figure 1. Micro-gravimètre (relatif) de terrain
Exemple de gravimètre relatif de terrain à ressort.
Il existe aussi des gravimètres dits absolus, dont certains gravimètres "supraconducteurs".
Les gravimètres sont de deux types : relatifs ou absolus.
Les gravimètres relatifs ne permettent pas d'avoir une valeur exacte de la pesanteur, mais ils sont très sensibles à ses variations. Ainsi, on peut cartographier avec précision la différence de pesanteur par rapport à un point choisi comme référence. Les gravimètres à ressort (une masse connue tire plus ou moins sur un ressort dont l'allongement est mesuré) ont une précision allant jusqu'à 10-8m.s-2 (environ 10-9g). D'autres gravimètres, à supra-conducteur (une masse en métal est mise en lévitation par un champ magnétique), sont encore plus précis, de l'ordre de 10-9m.s-2 (ou 10-10g).
Des gravimètres dits absolus mesurent la chute libre d'un corps au sein d'un dispositif assez complexe à mettre en œuvre mais aboutissant à une précision de l'ordre de 10-9g. Enfin, avec les satellites, la gravimétrie spatiale à vu le jour. La connaissance précise et en continu de l'orbite des satellites permet de tirer des informations sur le champ de pesanteur, avec ici possibilité de couvrir toute la surface de la Terre avec des mesures répétées. Le projet GOCE permettra une cartographie des océans avec une résolution spatiale de 100 km et une précision attendue de l'ordre de 1 à 2.10-6g, soit 1 à 2 mGal, ce qui revient à une précision de 1 à 2 cm sur la position de l'équipotentielle de pesanteur matérialisée par la surface des océans (interface libre entre deux fluides, l'eau et l'atmosphère).
Effet d'une perturbation locale de masse sur la pesanteur
Regardons l'effet de perturbations ponctuelles de masse dans un modèle de Terre.
Effet d'un excès local de masse sur la pesanteur et le potentiel de pesanteur
Considérons un modèle initial simple : équipotentielles parallèles et horizontales, et donc pesanteur verticale et de valeur constante sur une équipotentielle. Ce modèle simpliste correspond au champ de pesanteur sur une Terre homogène à symétrie sphérique ou ellipsoïde pour laquelle on fait une observation "locale", la courbure des équipotentielles peut alors être négligée.
Ajoutons, à ce modèle simple, une perturbation locale de distribution de masse et observons l'effet sur la pesanteur. Les schémas suivants illustrent le cas d'un excès de masse (E) ponctuel. Dans tous les schémas :
- h << r et d<<r, l'altitude et la distance à la masse ponctuelle sont petites devant la distance au centre de la Terre ;
- le point A représente un point "non perturbé" (car trop loin) et le point B, "perturbé", est situé à l'aplomb de la perturbation (même vecteur unitaire pour les effets de la Terre et de la masse ponctuelle, donc sommation aisée pour la démonstration) ;
- les équipotentielles ont le même écart de potentiel : W4-W3 = W3-W2 = W2-W1 = W1-W0
- les échelles horizontales et verticales ne sont pas respectées, de manières à garder une certaine lisibilité aux schémas.
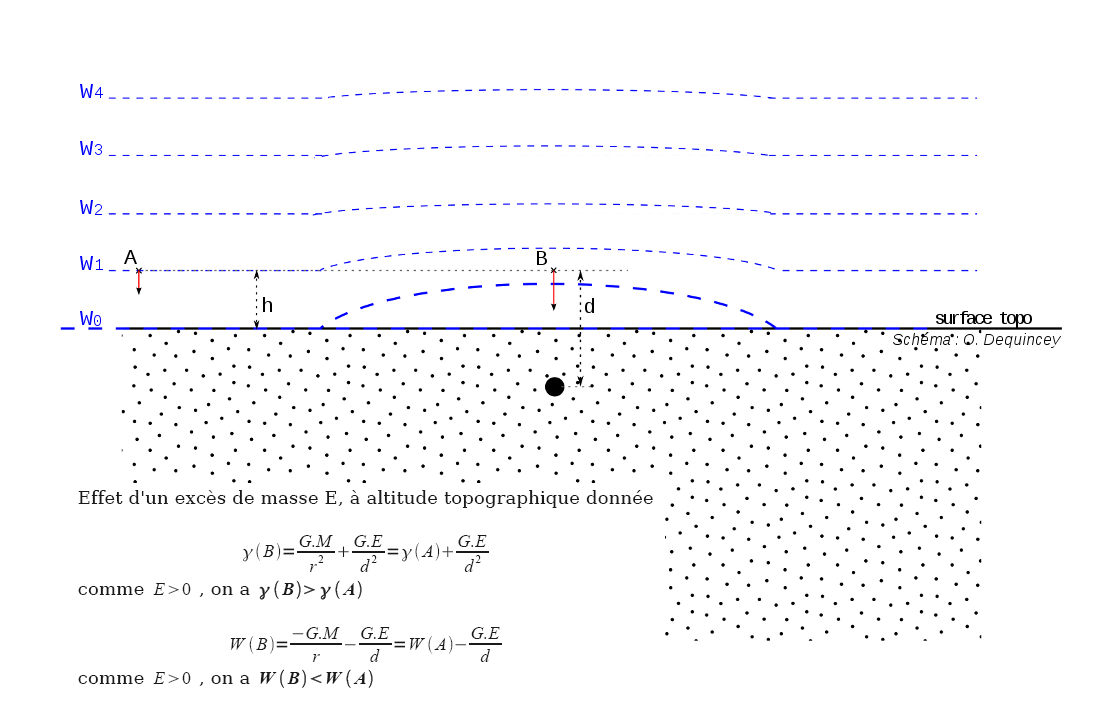
Figure 2. Effet d'un excès de masse local sur la pesanteur et le champ de pesanteur, à une altitude donnée
L'excès de masse ressenti en B, induit, à altitude constante, une pesanteur plus grande et un potentiel plus faible (équipotentielle "soulevée").
En B, comme en A, la pesanteur est verticale. Elle ne l'est pas de part et d'autre près de B, le vecteur pesanteur est dévié "vers la masse" provoquant ici un excès de masse.
Plaçons-nous d'abord à une altitude topographique donnée h et comparons pesanteur (ϒ) et potentiel de pesanteur (W) au deux points A et B.
À même altitude topographique, la pesanteur est plus forte à l'aplomb d'un excès de masse :
- ϒA = G.M/r2 et ϒB = G.M/r2 + GE/d2 = ϒA + GE/d2
- comme E>0 (excès de masse), alors ϒB > ϒA
- Remarque : l'excès de pesanteur décroît quand on s'éloigne de la perturbation.
À même altitude topographique, le potentiel de pesanteur est plus faible à l'aplomb d'un excès de masse :
- WA = -GM/r (en posant W∞=0) et WB = -GM/r - GE/d = WA - GE/d
- comme E>0 (excès de masse), alors WB < WA
- Remarque : le déficit de potentiel décroit quand on séloigne de la perturbation.
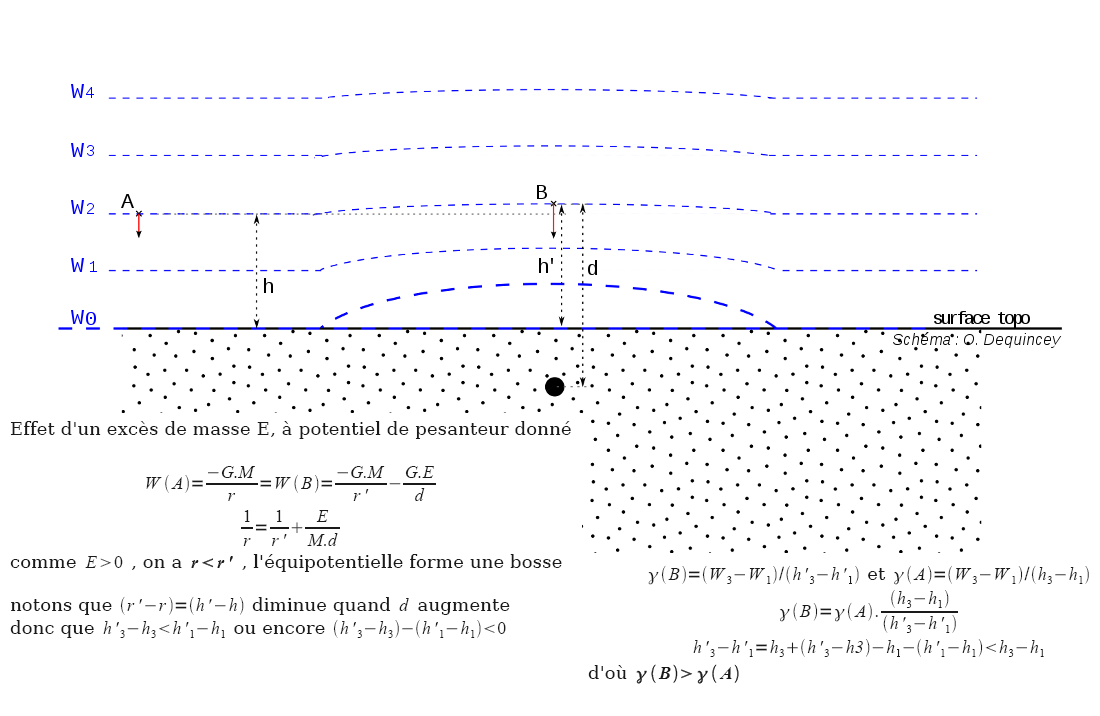
Figure 3. Effet d'un excès de masse local sur la pesanteur et le champ de pesanteur, à potentiel constant
L'excès de masse ressenti en B, induit, à potentiel constant, une pesanteur plus grande et une équipotentielle "soulevée".
En B, comme en A, la pesanteur est verticale. Elle ne l'est pas de part et d'autre près de B, le vecteur pesanteur est dévié "vers la masse" provoquant ici un excès de masse.
Plaçons-nous, maintenant, sur une équipotentielle W2, et comparons potentiel de pesanteur (W) et pesanteur (ϒ) aux points A (h, r) et B (h', r') de cette équipotentielle.
Une équipotentielle de pesanteur est "soulevée" à l'aplomb d'un excès de masse :
- WA = -GM/r = W2 = WB = -GM/r' - GE/d
- d'où M/r = M/r' + E/d soit 1/r = 1/r' +E/Md
- comme E>0 (excès de masse), alors E/Md>0 et donc 1/r>1/r', soit encore r<r'
- Remarque : la bosse, Δh=h'-h, diminue quand on s'éloigne de la perturbation.
Sur une équipotentielle de pesanteur, la pesanteur est plus forte à l'aplomb d'un excès de masse :
- La pesanteur ϒ dérive du potentiel W, donc on peut écrire "localement" (les numéos renvoyant à l'équipotentielle de même numéro) :
- ϒA = (W3-W1)/(h3-h1) et ϒB = (W3-W1)/(h'3-h'1)
- soit ϒB = ϒA.(h3-h1)/(h'3-h'1)
- h'3-h'1 = (h3 +Δh3) - (h1 +Δh1) = (h3-h1) - (Δh1 - Δh3)
- On a vu ci-dessus que la "bosse" diminue quand on s'éloigne de la perturbation, donc que Δh1>Δh3 , (Δh1 - Δh3)>0
- donc h'3-h'1 < h3-h1 soit (h3-h1)/(h'3-h'1)>1 , donc ϒB > ϒA
- Remarque : on montrerait que l'excès de pesanteur décroît quand on s'éloigne de la perturbation.
Généralisation
Un excès de masse local (non compensé par ailleurs) induit à l'aplomb de la perturbation une baisse du potentiel, un soulèvement local des équipotentielles (bosse d'équipotentielle) et une augmentation locale de la pesanteur, à altitude topographique constante comme à potentiel constant. Près de la perturbation, la déviation des équipotentielles indique que le vecteur pesanteur est "attiré" vers l'excès de masse.
De même, en prenant un déficit de masse D<0, on aurait montré ce qui suit.
Un déficit de masse local (non compensé par ailleurs) induit à l'aplomb de la perturbation une hausse du potentiel, un abaissement local des équipotentielles (creux d'équipotentielle) et une diminution locale de la pesanteur, à altitude topographique constante comme à potentiel constant. Près de la perturbation, la déviation des équipotentielles indique que le vecteur pesanteur est "repoussé" par le déficit de masse.
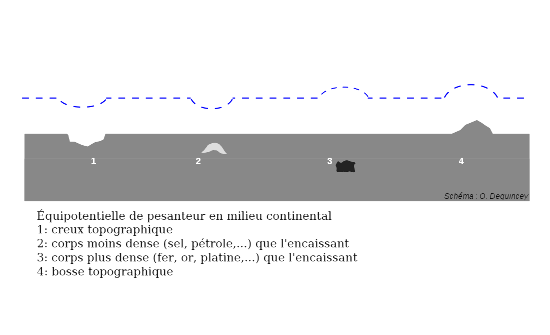
Les figures suivantes montrent les déviations d'une équipotentielle au-dessus d'un continent et d'un océan du fait de perturbations de masse locales et non compensées. Le cas 1 et 4 représentent un creux et une bosse topographiques de la surface continentale ou du fond de l'océan. Les cas 2 et 3 représentent la présence d'une masse moins dense (sel, eau, pétrole...) ou plus dense (minerai de fer, or, platine...) que l'encaissant. Pour l'océan, l'équipotentielle représentée est la surface océanique dont la position moyenne décrit une équipotentielle de pesanteur, appelée géoïde (voir ci-après).
Figure 4. Perturbation d'une équipotentielle au-dessus de la surface plane d'un continent 1 et 2, déficit de masse. 3 et 4, excès de masse. | Figure 5. Perturbation de la surface océanique, équipotentielle de pesanteur 1 et 2, déficit de masse. 3 et 4, excès de masse. |
Forme de la Terre et géodésie
La géodésie est la détermination de la forme "exacte" de la Terre à partir de mesures gravimétriques.
Forme théorique de la Terre et ellipsoïde de référence
Après l'abandon de l'idée d'une Terre plate pour une Terre sphérique, la prise en compte de la rotation de la Terre autour d'un axe a abouti à l'idée d'une Terre ellipsoïdale, c'est-à-dire une sphère déformée du fait de la rotation autour d'un axe de rotation. Des expéditions de mesure d'arc de méridien à l'équateur et aux hautes latitudes ont permis de trancher la discussion qui portait sur la forme de l'ellipsoïde - aplatissement aux pôles ou à l'équateur - en faveur d'un aplatissement aux pôles (voir l'article de V. Deparis sur l'évolution des idées à propos de la forme de la Terre, et la conférence de F. Chambat et I. Passeron sur la figure de la Terre au 18ème siècle).
La forme théorique de la Terre passe donc d'une sphère à un modèle en forme d'ellipsoïde de révolution aplati selon l'axe de rotation. Pour définir un ellipsoïde de référence, on considère une Terre formée d'enveloppes homogènes concentriques déformées seulement par la rotation de la Terre autour de son axe. De cette forme, et de la répartition des masses imposée, découle alors un modèle gravimétrique avec des équipotentielles ellipsoïdales et concentriques.
La Terre a, en bonne approximation, la forme d'un ellipsoïde de révolution avec les caractéristiques suivantes :
- aplatissement = 1/298,257 ;
- "rayon" polaire = 6356,75 km (demi-petit axe de l'ellipsoïde de révoution);
- "rayon" équatorial = 6378,14 km (demi-grand axe de l'ellipsoïde de révoution);
- champ de pesanteur en surface, aux pôles, γpôle = 9,83 ms-2 ;
- champ de pesanteur en surface, à l'équateur, Υéquateur = 9,78 ms-2.
Remarquons qu'une surface équipotentielle n'est pas une surface à champ constant ("pente" pas nécessairement constante de part et d'autre d'un chemin horizontal) ! Ainsi, lorsqu'on reste à la surface de cet ellipsoïde de référence, on se déplace sur une équipotentielle, mais la valeur de la pesanteur varie de 9,83 au pôle Nord à 9,78 m.s-2 à l'équateur. On est donc un peu plus lourd, de 0,5%, aux pôles qu'à l'équateur.
Forme "réelle" de la Terre et géoïde
Dans le modèle théorique, les équipotentielles, dont la surface de la Terre, sont des ellipsoïdes de révolution concentriques. Dans les faits, la répartition des masses à l'intérieur de la Terre est plus complexe (enveloppes non homogènes, mouvements de matière ascendants et descendants, anomalies thermiques...) que dans un modèle concentrique. Les équipotentielles de pesanteur ne sont donc pas exactement ellipsoïdales. La surface moyenne des océans (surface libre et à l'équilibre -pour le niveau moyen- entre deux fluides -eau / atmosphère) est une équipotentielle de pesanteur qui couvre 70% de la surface de la Terre et qui est, de ce fait, prise comme équipotentielle de référence, appelée géoïde.
La détermination du géoïde (= la géodésie) par altimétrie satellitaire, sur les océans, doit être complétée sur les continents. En partant d'un point connu du géoïde on peut le prolonger, plus vers l'intérieur des terres, par la mesure du vecteur pesanteur qui est en tout point perpendiculaire au géoïde (on utilise le fait que les lignes de champ sont perpendiculaires aux surfaces équipotentielles). Un exposé de la détermination du géoïde en milieu continental a déjà été proposé dans de précédents articles.
On parle parfois de bosses et creux du géoïde... alors que ce dernier définit une surface horizontale de référence, puisqu'en tout point perpendiculaire à la verticale donnée par la pesanteur. Il ne peut y avoir de bosse ou de creux du géoïde que par rapport à une autre forme, un ellipsoïde de référence.
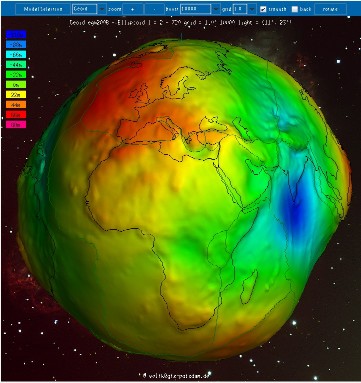
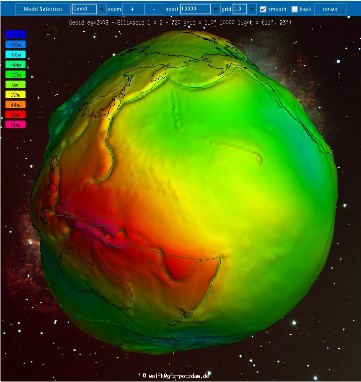
Source - © 2010 Wolfgang Köhler, ICGEM (menu "Gravity Visualization") Figure 6. Creux et bosses du géoide par rapport à un ellipsoïde de référence (1/4) On observe une bosse sur l'Atlantique Nord et un creux important au Sud de l'Inde. | Source - © 2010 Wolfgang Köhler, ICGEM (menu "Gravity Visualization") Figure 7. Creux et bosses du géoide par rapport à un ellipsoïde de référence (2/4) On observe une bosse du géoïde sur l'Ouest du Pacifique, du Japon à la Nouvelle-Zélande, en bordure de plaque. |
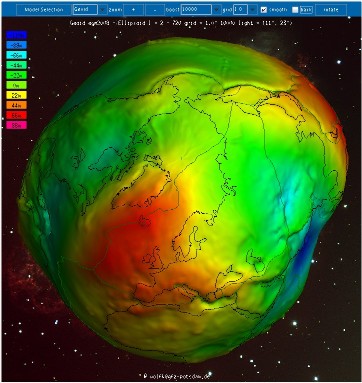
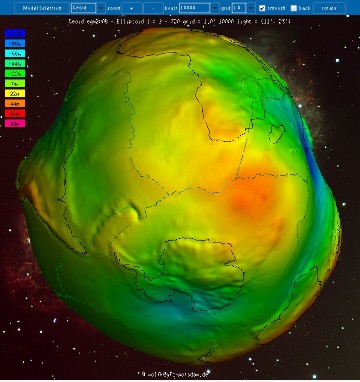
Source - © 2010 Wolfgang Köhler, ICGEM (menu "Gravity Visualization") Figure 8. Creux et bosses du géoide par rapport à un ellipsoïde de référence (3/4) Vue centrée sur le pôle Nord. | Source - © 2010 Wolfgang Köhler, ICGEM (menu "Gravity Visualization") Figure 9. Creux et bosses du géoide par rapport à un ellipsoïde de référence (4/4) On perçoit le creux du geoïde au Sud de l'Inde. Une bosse importante est observée le long de la côte occidentale de l'Amérique du Sud. |
Les bosses et creux mettent en évidence des excès et des déficits de masse par rapport au modèle "simple" de répartition des masses à l'intérieur de la Terre selon un ellipsoïde.
Petit aparté, altitude et distance au centre de la Terre
Les altitudes sont mesurées par rapport au géoïde (le niveau moyen des océans). Le point le plus élevé en altitude, donc par rapport au géoïde, est le sommet de l'Everest (8848 m). Du fait de la forme de la Terre, aplatie aux pôles et "renflée" à l'équateur (cf. ci-dessus, le rayon équatorial est environ 21 km plus grand que le rayon polaire), le sommet de l'Everest, vers 28° de latitude Nord, n'est par contre pas le point topographique le plus éloigné du centre de la Terre. C'est en effet le Sommet du Chimborazo, en Équateur, situé vers 2° de latitude Sud, qui avec ses 6268 m d'altitude est à plus de 6384 km du centre de la Terre contre 6382 km pour le sommet de l'Everest.
Gravimétrie : corrections, anomalies et intérieur de la Terre
Mesures et corrections
La pesanteur dépend de la position du point de mesure (distance au centre de la Terre ou altitude, et latitude) et des masses "ressenties" à ce point (Terre "moyenne" et perturbations diverses). Afin de ne garder d'une mesure que la partie renseignant sur les masses "invisibles" en profondeur on la corrige des effets superficiels, et connus : altitude et relief.
Pour corriger l'effet de l'altitude, on se replace par le calcul sur un ellipsoïde de référence d'altitude égale à 0 (γ0, r0). On parle de correction à l'air libre. Elle tient compte de l'altitude h à laquelle a été effectuée la mesure et vaut 2.h.γ0/r0.
Pour corriger l'effet de masse d'un relief, on enlève par le calcul la masse de roche comprise entre l'altitude h et l'altitude 0. On parle de correction de plateau. Elle dépend de l'altitude h et de la masse volumique ρ de la roche (connue ou estimée) et est égale à 2π.G.ρ.h.
De manière plus complète, on peut effectuer une correction de topographie qui prend en compte les reliefs entourant le point de mesure. Cette correction se fait d'après une carte topographique et selon des abaques prenant en compte le type (pic, vallée...) et la distribution spatiale des reliefs autour du point de mesure.
On appelle correction de Bouguer (1698-1758) la prise en compte de ces 3 corrections, la correction "simple" de Bouguer n'incluant pas la correction topographique.
Dans le cas particulier de la comparaison de 2 points de latitudes très différentes, on effectue, de plus, une correction de latitude (effet de la force centrifuge).
Ces corrections effectuées, on est ramené à une valeur que l'on peut comparer à la valeur attendue dans le cadre de l'ellipsoïde de référence choisi. Tout écart à ce modèle porte une information sur les écarts entre répartition réelle et répartition théorique des masses en profondeur.
Des anomalies pour sonder l'intérieur de la Terre
On appelle anomalie la différence entre une valeur mesurée corrigée et sa valeur "théorique".
Ainsi, une anomalie nulle (valeur corrigée = valeur théorique) indique que le modèle rend bien compte des observations, du moins au(x) point(s) de mesure considéré(s).
Une anomalie négative (valeur corrigée < valeur théorique) indique que la pesanteur est plus faible que ce que prévoit le modèle (ça "attire" moins que prévu), il y a donc un déficit de masse "local" par rapport au modèle.
Une anomalie positive (valeur corrigée > valeur théorique) indique que la pesanteur est plus forte que ce que prévoit le modèle (ça "attire" plus que prévu), il y a donc un excès de masse "local" par rapport au modèle.
Classiquement, l'existence d'anomalies négatives dans une chaîne de montagne a conduit au développement du concept d'isostasie : la croûte est considérée comme flottant sur un manteau fluide et la surface topographique dépendrait de l'épaisseur de la croûte sous-jacente ou de la masse volumique de celle-ci. En 1851, Airy proposa que la croûte, de masse volumique constante, était plus épaisse sous les chaînes de montagne. Ainsi, l'excès de masse apparent lié au relief de la montagne serait accompagné en profondeur par une racine crustale, de la croûte remplaçant alors du manteau plus dense, créant un déficit de masse compensateur. Peu après, Pratt proposa une alternative : à épaisseur de croûte constante, les anomalies observées indiqueraient des variations latérales de densité de la croûte, plus la croûte est dense, moins il y aurait de relief. Aujourd'hui, avec l'apport des coupes sismiques, on sait que des racines crustales sont présentes sous les montagnes, mais aussi que des variations latérales de densité existent et expliquent une partie des anomalies gravimétriques.
Si l'isostasie permet d'expliquer les anomalies de moyenne longueur d'onde (chaînes de montagnes, fosses océaniques...) par des réajustements à l'échelle de la croûte ou de la lithosphère, des anomalies de très courte longueur d'onde et d'autres de grande longueur d'onde subsistent.
Les anomalies de courte longueur d'onde indiquent généralement la présence de perturbations de masse superficielles (les premiers hectomètres à kilomètres). C'est le domaine de la prospection. La gravimétrie relative permettant de détecter de petites variations de la pesanteur, elle apporte des arguments à la présence éventuelle de matériaux peu denses (eau, pétrole, gaz, sel...) créant des déficits de masse, ou, à l'opposé, la présence de filons de minérais denses (fer, or, platine...) créant des excès de masse. Ces études sont associées à des études sismiques qui aboutissent à la définition de points de forages de prospection.
Les anomalies de grande longueur d'onde (typiquement les "anomalies" du géoïde par rapport à un ellipsoïde de référence) indiquent la présence en profondeur d'anomalies de densité par rapport à une distribution symétrique (ellipsoïdale). Elles sont à mettre en relation avec les mouvements de matière dans le manteau et avec les hétérogénéités latérales de température.
Quelques pistes pour fureter sur le web
Cours, exercices, données de géophysique, avec de la gravimétrie, site personnel de F. Chambat, page enseignement.
Cours et didactiels du BGI (Bureau Gravimétrique International).
Données gravimétriques du BRGM, parmi beaucoup d'autres.
La "gravithèque" du site FROG (lié au projet d'altimétrie satellitale GOCE). Voir les cours et ne pas hésiter à tester les autres rubriques.
Visualisation du géoïde sur la site de l'ICGEM (International Centre for Global Earth Models) : menu "Gravity Visualization"