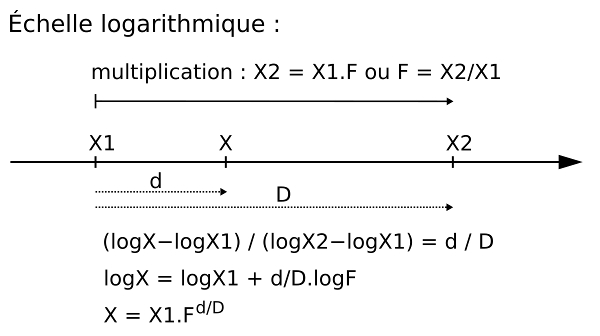Article | 27/05/2021
Le diagramme de phase de l’eau, un classique qui manque parfois de repères
27/05/2021
Résumé
De l’importance des échelles choisies pour tracer une courbe. Échelle linéaire, échelle logarithmique et interprétation de courbes de fonctions usuelles.
Table des matières
Article faisant suite à des échanges avec des enseignants confrontés à des diagrammes très répandus mais difficiles à comprendre et à utiliser car “faux”.
Au départ, une question essentielle et un diagramme de phase “classique”
Le diagramme de phase de l’eau est un incontournable pour comprendre les conditions de présence d’eau liquide sur Terre mais aussi dans le système solaire, l'eau liquide étant l'un des critères de base pour rendre possible la présence de vie de type terrestre. Cependant ce diagramme ne suffit pas à expliquer la présence de vapeur d'eau à des températures inférieures aux températures d'ébullition. Il faut pour cela prendre en compte la notion d'évaporation et de pression de vapeur saturante (pression maximale de vapeur d'eau dans un gaz en équilibre avec de l'eau liquide, pression dépendant des conditions de pression et de température)… ce qui explique que le linge sèche à pression ambiante sans être porté à 100°C.
Pour ces considérations, il est possible de revoir les articles de Planet-Terre traitant déjà de ces aspects : par exemple, De l'eau en ébullition dans une bouteille à basse température et basse pression : manipulation simple, geysers et autres analogies géologiques, ainsi que De l'eau à haute pression dans une presse à enclumes de diamant et de la glace à température ambiante, analogies avec le magmatisme et le métamorphisme, sans oublier Vapeur d'eau à la surface de la Terre et des planètes : distinction entre ébullition et évaporation, ou encore L'état supercritique en sciences de la Terre.
C'est l'apparition de la figure ci-dessous dans une discussion avec un enseignant qui soulevé le problème de savoir d'où venait la différence entre ce diagramme ceux que l'on trouve dans les articles cités dans le paragraphe précédent (des diagrammes “justes” sont redonnés en fin d'article).
Source - © 2016 ftrouillet / ACCES
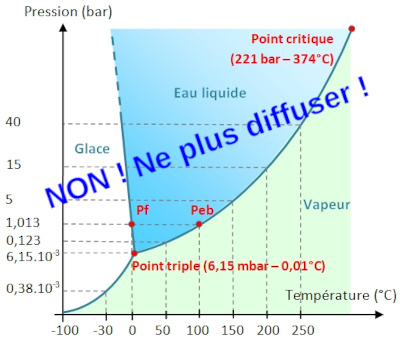
Figure 1. Un diagramme trop classique à ne plus propager
Ce diagramme adapté d'un diagramme répandu semble “normal” même si à y regarder de plus près on remarque vite soit qu'il est faux, soit qu'il n'a pas été adapté correctement. À ne plus diffuser en l'état.
Les échelles de pression et de température ne sont ni linéaires, ni logarithmiques (voir plus loin)… Diagramme pour le moins atypique !
Un souci assez vite décelé est celui des échelles des axes : elles ne sont ni linéaires ni logarithmiques mais… fantaisistes ?
Revenons d'abord sur les échelles dans les graphiques avant d'analyser ce diagramme, de tenter d'en comprendre la genèse et de proposer une représentation utilisable.
Repères à échelles linéaires ou logarithmiques et courbes usuelles
Rappelons d'abord comment sont construites les échelles des axes des graphiques couramment utilisés. On distingue les échelles linéaires et les échelles logarithmiques.
Pour un axe à échelle linéaire, une distance donnée entre 2 points correspond à une différence de valeur fixe : plus la distance est grande, plus la différence est grande. Par contre, pour un axe à échelle logarithmique, une distance donnée entre 2 points correspond à un rapport de valeur fixe : plus la distance est grande, plus le rapport est grand.
Dans ce qui suit, la notation “log” correspond à la fonction logarithme à base 10, définie comme la fonction réciproque de la fonction 10x.
Illustrons ce propos en exprimant la valeur “x” d'un point de l'axe situé entre les points de valeur x1 et x2 (x1 < x < x2). On notera “D” la distance sur l'axe entre les points de coordonnées x1 et x2, et “d” celle entre les points de coordonnées x1 et x.
Pour une échelle linéaire, notons “A” la différence x2 − x1 , soit x2 − x1 = A. Le rapport des différences des valeurs est proportionnelle au rapport des distance entre les points. On a donc, (x − x1) / (x2 − x1) = d/D, ce qui revient à (x − x1) / A = d/D, soit encore x = x1 +A.d/D. Pour un point situé “au milieu de x1 et x2, on alors x = x1 + A/2, soit x = (x1 + x2)/2 (coordonnée du milieu), et pour un point situé aux deux tiers entre x1 et x2, on obtient x = x1 + 2.A/3, soit x = (x1 + 2.x2)/3.
Figure 2. Coordonnées sur une échelle linéaire
Si on note “a” la différence (x − x1) on a a= d/D.A ou encore d= D.a/A.
Connaissant D et A, on en déduit a si on mesure d, ou on calcule d pour une différence a donnée.
Pour une échelle logarithmique, rappelons une propriété essentielle des logarithmes : log(a.bn) = log(a) + n.log(b). Notons ici “F” le facteur multiplicatif entre x1 et x2, soit x2 / x1 = F. Cette égalité s'écrit aussi log (x2) − log(x1) = log(F). À la différence fixe des valeurs pour l'échelle linéaire correspond donc une différence fixe des logarithmes des valeurs pour l'échelle logarithmique. C'est alors le rapport des différences des logarithmes des valeurs qui est proportionnel au rapport des distances entre les points. On a donc (log(x) − log(x1)) / (log(x2) − log(x1)) = d/D, ce qui revient à log(x/x1) / log(F) = d/D, soit encore log(x/x1) = (d/D).log(F) = log(Fd/D). Cette dernière équation revient à x/x1 = Fd/D soit, finalement, x = x1.Fd/D. Pour un point situé “au milieu” de x1 et x2, on alors x = x1.F1/2, et pour un point situé aux deux tiers entre x1 et x2, on obtient x = x1.F2/3. Pour F=10, on a alors un point du milieu ayant une valeur x égale à environ 3,16.x1 (soit 101/2.x1) et un point aux deux tiers avec une valeur d'environ 4,64.x1 (soit 102/3.x1).
Figure 3. Coordonnées sur une échelle logarithmique
Si on note “f” le rapport x/x1 on a alors log(f) = d/D.log(F) (soit (f = Fd/D) ou encore d = D.log(f)/log(F).
Connaissant D et F, on en déduit f si on mesure d, ou on calcule d pour un rapport f donné.
Pour une échelle logarithmique classique pour laquelle on mesure D pour F=10, on a alors f=101/2~3,16 pour d=1/2.D. Dans l'autre sens, on a d~0,3.D pour f=2 et d~0,7.D pour f=5.
L'usage des échelles linéaires et logarithmiques n'a pas qu'un impact sur le mode de calcul des coordonnées d'un point dans un graphique, mais aussi sur l'aspect des courbes. Ainsi, si l'on dit souvent qu'une droite est la représentation graphique d'une fonction affine (y=a.x+b), c'est qu'on se place par principe dans un repère linéaire, c'est à dire dont les 2 axes ont des échelles linéaires.
Le logarithme de zéro n'étant pas défini, un axe ne peut avoir une échelle logarithmique que s'il correspond à un paramètre dont les valeurs sont toujours positives ou toujours négatives, mais ne passent jamais par zéro. Pour un axe de température, on comprend alors l'intérêt de l'usage de la température absolue en kelvins (K) si on veut utiliser ce type d'échelle.
Pour se convaincre de l'importance des échelles utilisées sur l'aspect des courbes de fonctions “simples”, quatre fonctions “classiques” (affine, exponentielle, logarithmique et sinusoïde) ont été représentées dans quatre repères : un repère linéaire (2 échelles linéaires), deux repères semi-logarithmiques (une échelle linéaire et l'autre logarithmique), l'un log-linéaire (ordonnées logarithmiques) et l'autre linéaire-log (ordonnée linéaire), et un repère logarithmique ou repère log-log (2 échelles logarithmiques). Jugez vous-même.
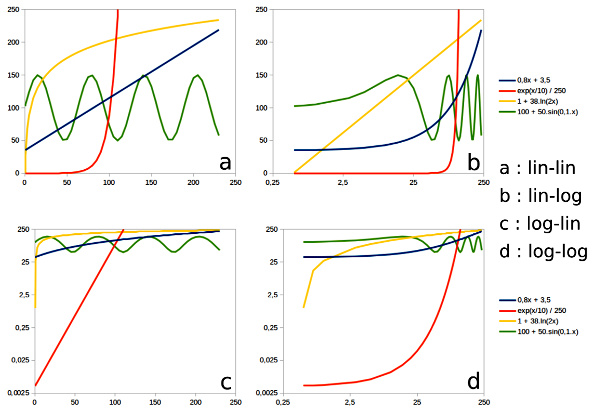
Figure 4. Quelques fonctions simples représentées dans des repères mêlant échelles linéaires et logarithmiques
On voit très bien que l'aspect des courbes dépend du repère et des échelles choisis. Nous sommes généralement plutôt habitués aux repères linéaires (lin-lin).
On observe qu'une droite est bien une fonction affine dans un repère linéaire (lin-lin), mais correspond à un logarithme dans un repère lin-log ou à une exponentielle dans un repère log-lin. Qui parierait sur une fonction sinusoïdale simple (strictement périodique) en voyant les courbes vertes dans les repères lin-log et log-log ? La fonction affine n'est pas facile à “détecter” dans les repères non linéaires.
Figures séparées lin-lin, lin-log, log-lin, log-log. Vous est proposé le fichier ods ayant servi à établir ces courbes (pour en faire d'autres selon ses besoins).
Le ”bon” diagramme et l'origine possible de l'erreur
Revenons au diagramme de phase de l'eau posant problème et analysons-le.
Concernant l'axe des abscisses, l'échelle semble être linéaire d'après les graduations indiquées de −100°C à +250°C. Mais si on repère sur l'axe la position du point critique on arrive à une température de l'ordre de 320°C et non pas presque 375°C. Une petite erreur de graduation de l'axe lors de l'adaptation du graphe originel ?
Pour l'axe des ordonnées, on peut comparer les longueurs et les facteurs multiplicatifs pour plusieurs couples de points. Condition nécessaire mais pas suffisante, plus la distance entre deux points est grande, plus le facteur multiplicatif doit l'être aussi. Prenons les points de pression croissante 1,013, 5, 15 et 40. On a un facteur multiplicatif de ~5 entre 1,013 et 5, de 3 entre 5 et 15, et de 2,67 entre 15 et 40, mais les distances entre les points sont dans les proportions 9, 13, 17. Les distances augmentent quand les rapports diminuent… Ce n'est pas une échelle logarithmique (le fait qu'elle n'est pas linéaire saute aux yeux). Un autre test est de partir des pressions “certaines” pour vérifier la position d'autres valeurs. Les deux pressions assurées sont celle du point triple (6,15.10−3 bar) et celle du point critique (221 bar). Le facteur multiplicatif est de l'ordre de 35935. Tentons de trouver la position sur l'axe de la pression terrestre “standard” (1,013 bar). On utilise alors l'équation (log(x) − log(x1)) / (log(x2) − log(x1)) = d/D avec, ici x1=6,15.10−3, x=1,013, x2=221. On obtient d/D=0,4866, ce qui signifie que, sur l'axe des ordonnées, le point 1,013 devrait être presque à la moitié de la distance entre point triple et point critique. On n'y est pas, cela se voit, ce que l'on peut “vérifier” en mesurant le rapport d/D sur le graphique, de l'ordre de 0,157.
Le diagramme a donc des axes à échelles ni linéaires, ni logarithmiques !
La genèse de ce diagramme semble cependant pouvoir être élucidée. En effet, on trouve en fouillant un peu de “bons” diagrammes en cherchant sur le web. Notons la page Diagramme de phase du site Futura Sciences, sur laquelle on trouve à la fois un diagramme de phase de l'eau étendu aux hautes pressions et utilisable pour bien des illustrations, ainsi qu'une figure intitulée “Diagramme de phase d'un corps pur”, attribuée à l'Université de Sherbrooke (Québec, Canada) qui pourrait être un exemple de figure originelle “générale” à partir de laquelle des adaptations diverses pour l'eau ont constitué autant de dérives, faute de temps pour approfondir le sujet.
À partir d'un tel diagramme général de “corps pur” aux basses pressions, on peut le reprendre et attribuer aux points triple et critique les valeurs du corps étudié. Ce faisant on oublie de modifier au passage les tracés exacts des limites de phase. Par exemple, la limite solide-liquide a un pente inversée entre l'eau (ici dans le bon sens) et le CO2 (limite qui aurait été dans le “mauvais” sens si on avait utilisé ce diagramme “corps pur” pour l'adapté au CO2), les autres limites sont convexes ou concaves selon les corps considérés (voir, en illustration, les figures 1 et 2 de L'état supercritique en sciences de la Terre). On obtient alors un mauvais diagramme de phase de l'eau avec 2 points de coordonnées connues. Mais pour des besoins d'illustration, il est alors décidé de positionner d'autres points discutés dans le cours ou l'article. Pour placer ces points, il faut graduer les axes. Le plus simple est l'axe des températures, généralement linéaire. Une erreur, d'étourderie sans doute, fait que l'axe des abscisses est mal gradué. Ensuite, pour positionner les autres points, il suffit de partir de la température : en plaçant le point d'ébullition à 100°C, on a immédiatement la position de la pression à 1,013 bar et donc la pression standard à la surface de la Terre. De même pour les autres points. Malheureusement, la courbe liquide-vapeur étant concave sur le graphique alors qu'elle est convexe en réalité pour l'eau, le point de pression 1 bar se trouve placé trop bas. Même la légère erreur sur la température, qui décale le point 100°C vers la droite et remonte donc le point d'ébullition recherché, ne permet pas de corriger l'erreur fondamentale qui a consisté a prendre un diagramme de phase quelconque comme point de départ pour ensuite l'adapter avec plus ou moins de succès. Le diagramme discuté n'est certainement pas le diagramme originellement fautif, il a certainement été repris d'une autre source qui en avait repris une autre… Finalement, au bout de quelques reprises, ce diagramme diffuse et, lorsqu'un utilisateur recherche un diagramme de phase de l'eau, il trouvera des diagrammes très proches, tous faux, mais qui chacun légitime les autres. Si jamais, le “bon” diagramme est aussi trouvé, il apparaitra “bizarre” et souvent, faute de temps, c'est le nombre qui emportera la décision pour savoir lequel prendre.
Pour illustrer vos cours, exercices… il est cependant préférable de partir de données justes et donc “utilisables”.
Source - © 2011 Olivier Dequincey
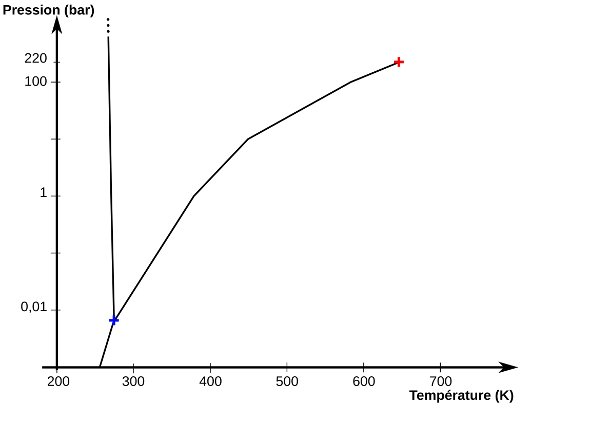
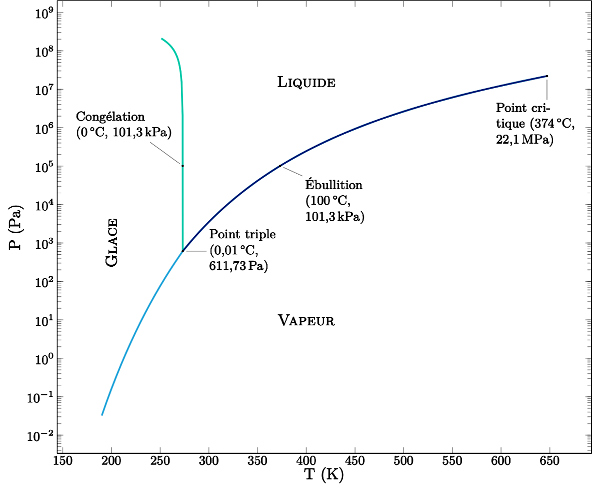
Figure 5. Exemple de diagramme de phase de l'eau pour les basses pressions
Diagramme semi-logarithmique simple à compléter selon ses besoins.
Le fichier ods ayant servi à établir les courbes usuelles dans plusieurs repères contient aussi une page avec de quoi tracer un diagramme de phase de l'eau (avec plus de points de traçage que pour celui proposé ici) et le visualiser dans ces différents repères. Les données utilisées dans ce fichier sont extraites du site The Engineering Toolbox, et ses pages Water Boiling Points at Higher Pressure, Water - Boiling Points at Vacuum Pressure et Ice / Water - Melting Points at Higher Pressure.
Figure 6. Diagramme de phase de l'eau semi-logarithmique pour les relativement basses pressions
Diagramme semi-logarithmique simple à compléter selon ses besoins.