La magnitude d'un séisme : définitions, déterminations

Lorsqu'un séisme frappe une zone habitée, il est comparé aux précédents sur la base du nombre de morts, du coût économique de la reconstruction, de la difficulté d'accès (destruction des infrastructures de transport), du nombre de personnes à reloger... La comparaison des séismes en fonction des dégâts occasionnés établit une échelle des intensités (type échelle de Mercalli ou échelle MSK avec des intensités allant de I à XII). Une telle échelle, idéale pour les impacts sur l'activité humaine, a de nombreuses limitations pour l'étude scientifique des séismes : seuls les séismes impactant des zones habitées sont pris en compte ; l'intensité dépend du type d'habitation (normes para-sismiques, nombre d'étages des constructions,...) mais aussi de facteurs géologiques locaux (nature du substratum,...). Cependant, cette échelle d'intensité reste la seule échelle de comparaison disponible pour les séismes historiques "anciens", c'est-à-dire antérieurs à la mise en place des réseaux sismiques (voir, par exemple, le séisme de Lambesc de 1909). En l'absence d'autres données, les cartes d'intensités isosismiques permettent aussi de déterminer la direction des failles ayant joué, ce qui complète par exemple un mécanisme au foyer donnant deux plans potentiels (voir, par exemple, le séisme de L'Aquila de 2009).

Dans les cas favorables, des données de terrain permettent d'estimer la "puissance" du séisme : connaissance du type de roche ayant "rompu", de la taille du plan de faille et du déplacement maximal le long de ce plan (observation de failles en surface). Là aussi, des limitations existent. Seuls sont concernés les séismes terrestres affectant des zones d'accès facile et ayant laissé des traces importantes et observables.

Aujourd'hui, tout séisme est observé par un réseau mondial de sismomètres (plusieurs réseaux nationaux et régionaux échangeant leurs informations). Pour chaque séisme on peut donc avoir des sismogrammes classiques, c'est-à-dire montrant la succession ondes P puis ondes S et enfin ondes de surface avec des amplitudes ni trop élevées (trop près de l'épicentre), ni trop faibles (trop loin de l'épicentre).

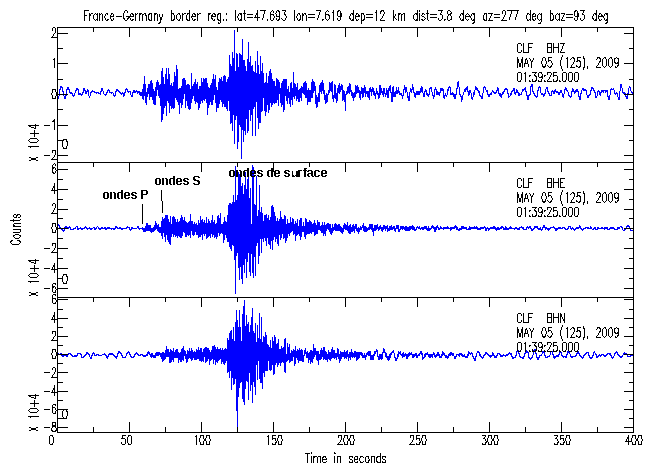
Source - © 2010 Observatoire GÉOSCOPE

Figure 1. Un sismogramme du séisme du 5 mai 2009 en Allemagne (près de la frontière avec la France)

Il y a trois enregistrements, un pour les mouvements verticaux (Z) et deux selon deux axes horizontaux (E et N). Station sismique de Chambon la Forêt, vers Orléans.

Sur ce sismogramme, le décalage temporel entre l'arrivée des ondes P et S, dont les vitesses respectives sont connues, renseigne sur la distance à l'épicentre (ici environ 420 km). Pour une distance épicentrale donnée, l'amplitude des ondes varie en fonction de l'énergie sismique libérée.

Sur la base d'un sismogramme (ou de la combinaison de sismogrammes, ou du sismogramme reconstruit dans la direction du rai sismique), on peut, par exemple, estimer la distance épicentrale et mesurer l'amplitude maximale des ondes de surface. À l'aide d'un abaque ou d'une formule empirique, on peut exprimer ces données extraites en une magnitude qui permettra de comparer les différents séismes. Quelques minutes après un séisme majeur, les observatoires sismologiques sont en mesure de donner une magnitude (ou une fourchette de magnitude), avant d'avoir la moindre idée de ce qui s'est passé sur le terrain. Connaître le plus tôt possible l'énergie d'un séisme est capital, par exemple, si l'on veut évacuer préventivement des zones susceptibles d'être affectées par un tsunami.

La comparaison des séismes nécessite, pour utiliser la même magnitude dans un réseau sismique, une calibration des sismomètres afin de prendre en compte les différents types de matériel et les effets géologiques locaux des stations sismiques. Plusieurs échelles de magnitude ont été développées. Selon les échelles, on prend en compte l'amplitude maximale des ondes des surface, ou celle des ondes S voire des ondes P, ou bien non pas une valeur maximale mais une valeur intégrée sur 1 à 20 secondes. L'atténuation différentielle des ondes en fonction de la distance à l'épicentre, la saturation possible des sismomètres pour les séismes puissants (dépendant aussi du type d'onde mesuré), la faible résolution pour les séismes lointains, expliquent que les différentes échelles développées sont adaptées à des gammes de puissances sismiques différentes et complémentaires : pour une puissance donnée, l'échelle la plus adéquate est celle qui a la meilleure sensibilité. Par exemple, l'échelle historique de Richter et Gutenberg (Richter 1935 puis Richter et Gutenberg en 1936 puis1956) est bien adaptée aux séismes de magnitude 2 à 6.

Le développement des sismomètres, qui mesurent aussi désormais des accélérations en plus des déplacements, a abouti à de nouveaux modes de calculs, à des calibrations avec les anciens sismomètres et à la définition de nouvelles échelles (surtout pour les forts séismes). Les formules de calcul de magnitudes utilisées ont été déterminées de façon à ce que les échelles soient complémentaires et que les magnitudes données soient comparables si on utilise deux échelles a priori adaptées à la détermination de la puissance d'un séisme. Par exemple, la formule de calcul de Kanamori (1977) (magnitude de moment) est telle qu'un séisme de magnitude 5 correspond exactement à un séisme de magnitude 5 sur l'échelle de Richter.

Ainsi, quelque soit le mode précis de calcul de la puissance d'un séisme, on peut parler de « magnitude sur l'échelle de Richter ». Dans les faits, ce sera une magnitude de Richter au sens strict ou bien une magnitude rapportée à une échelle de Richter "élargie". La précision d'une magnitude est de l'ordre de 0,25 degré de magnitude. Souvent, une première estimation est ensuite affinée au fur et à mesure de l'accumulation des données des différents réseaux sismiques.

Toutes les échelles sont logarithmiques. Ainsi, un séisme de magnitude 5 est "beaucoup plus puissant" qu'un séisme de magnitude 4, et non pas "25% plus puissant" ce qui serait le cas d'une échelle linéaire. Nous reviendrons sur ce point plus loin.

D'un point de vue physique, un séisme est aussi l'expression de la dispersion d'énergie via des ondes sismiques Un séisme peut aussi être vu comme le résultat de l'application d'un moment sismique dont seule une partie, l'énergie sismique, est dispersée sous forme d'ondes sismiques ; le reste de l'énergie provoquant des fractures, des déplacements et de la chaleur par friction.

Le moment sismique (en N.m) est défini comme le produit M₀ = μ.S.d ; avec "μ" la rigidité de la roche (en N.m^-2), "S" la surface du plan de faille ayant rompu (en m²) et "d" le déplacement le long de ce plan (en m). D'où une estimation possible via les données de terrain mais aussi par traitement des données de sismogrammes. Remarquons que l'usage utilise le N.m pour l'expression d'un moment qui est un travail et donc une énergie (1 N.m = 1 J).

Énergie sismique et moment peuvent être déterminés selon les sismomètres disponibles. Richter avait aussi proposé une estimation de l'énergie sismique à partir de la magnitude, à partir d'une relation empirique.

Magnitude (M), énergie sismique (E_s) et moment sismique (M₀) sont donc reliés par des équations. Les équations données ci-dessous, diffèrent parfois des formules que l'on peut trouver en faisant un peu de bibliographie (ou en furetant sur la toile), et cela pour deux raisons principales :

Magnitude - moment sismique :

Magnitude - énergie sismique :

Énergie sismique - moment sismique :

Revenons sur la "puissance" des séismes. Nous avons vu que la comparaison des dégâts se fait via l'échelle d'intensité Mercalli ou MSK. Voyons maintenant ce que signifie la magnitude pour comparer deux séismes en terme d'énergie libérée.

Soit deux séismes de magnitude M₁ et M₂, tels que M₂ = M₁ + A, les formules précédentes permettent de comparer les énergies (totales M₀ ou sismiques E_s) dégagées par ses deux séismes.

M₂ - M₁ = A --> 2/3.log₁₀(E_s2) -2/3.log₁₀(E_s1) = A, soit log₁₀(E_s2) - log₁₀(E_s1) = log₁₀(E_s2/E_s1) = 3/2.A, soit encore (E_s2/E_s1) = 10^3/2.A

On remarque immédiatement, qu'une différence de 2 degrés de magnitude (A=2) correspond à une énergie sismique 1000 fois plus importante (10³).

On retrouve la même formule en remplaçant E_s(énergie sismique) par M₀(moment sismique). Appliquons la formule précédente pour comparer des magnitudes et des énergies sismiques de séismes.

Remarquons ici que la précision de l'ordre de 0,25 degré de magnitude correspond à une détermination de la quantité d'énergie à un facteur 2 près, ce qui peut sembler énorme, mais reste faible quand on compare deux séismes séparés par plus d'un degré de magnitude.

Si l'on prend le séisme de magnitude 7 à Haiti du 12 janvier 2010 (M=7) comme référence, alors le séisme du Sichuan de mai 2008 (M=7,9) est 22,4 fois plus énergétique, le séisme du 27 février 2010 au Chili (M=8,8) l'est 500 fois plus, et le séisme "record" de 1960 au Chili (M=9,5) 5600 fois plus.

Il existe une comparaison usuelle entre séisme et bombes, telle qu'une bombe atomique d'une kilotonne de TNT correspond à un séisme de magnitude 4. Cette comparaison implique, si on reprend la formule magnitude - énergie sismique et qu'on trouve l'équivalence TNT - énergie (1g de TNT équivaut à 1000 calories, soit 4184 J), qu'il est considéré dans cette "analogie" empirique que seul 0,5 % (1/200) de l'énergie de la bombe est propagée sous forme sismique. La conversion de la totalité de l'énergie "explosive" en énergie sismique aboutirait donc à un séisme 200 fois plus énergétique, soit, pour une bombe d'une kilotonne de TNT, à un séisme de magnitude 5,5(3).

La bombe Little Boy, ayant explosé au-dessus d'Hiroshima le 6 août 1945, avait une puissance de 15 kilotonne de TNT. L'énergie de cette bombe correspond donc soit à un séisme de magnitude ~4,8 (comparaison usuelle des bombes), soit à un séisme de magnitude 6,3 (toute l'énergie en énergie sismique).

La comparaison bombe - séisme permet ici de rappeler que le développement important des réseaux sismiques et de sismomètres de plus en plus performants (pouvant enregistrer des séismes éloignés) après la Seconde Guerre Mondiale tient en partie à la volonté des deux blocs d'alors de détecter les essais de bombes nucléaires de l'autre bloc. Les mesures lors de ses propres essais permettaient d'estimer la fraction d'énergie propagée sous forme d'énergie sismique en fonction du type et des conditions des essais. Ainsi, via les séismes engendrés lors des essais, il était possible de compter les essais de l'autre camp et d'estimer la puissance maximale des bombes testées.

Les équivalences magnitude - énergie, permettent de comparer les énergies sismiques à des quantités d'énergies naturelles ou anthropiques (chute d'astéroïde, volcanisme, énergie solaire, production / consommation d'énergie...).

Comparons, par exemple, l'énergie sismique des 4 séismes précédemment cités avec l'énergie cinétique d'une météorite arrivant au sol. Pour une météorite chondritique de densité 3,3 et de vitesse d'arrivée au sol de 30 km/s, les séismes d'Haiti, du Sichuan, du Chili en 2010 et du Chili en 1960, correspondent à des météorites de diamètres respectifs de 2,4 m, 6,7 m, 18,9 m et 42,3 m qui laisseraient des cratères de diamètres respectifs de l'ordre de 50 m, 130 m, 400 m et 850 m (en prenant un cratère environ 20 fois plus grand que la météorite).

On peut aussi faire un calcul dans l'autre sens. À la limite Crétacé-Tertiaire, ayant vu la disparition entre autres des Dinosaures, une météorite d'une dizaine de kilomètres de diamètre, ayant engendré un cratère de 200 km, s'est abattue sur Terre. Son énergie cinétique, selon les mêmes hypothèses que ci-dessus, correspond à l'énergie sismique libérée par un séisme de magnitude 13(,05) ou au moment sismique d'un séisme de magnitude 9,9 (ce qui est ici certainement plus proche de la magnitude du séisme engendré par l'impact car l'essentiel de l'énergie a été dissipée pour sublimer la météorite, "creuser" le cratère, fondre des roches, projeter des éjectas...).

De même, l'éruption plinienne du volcan indonésien Krakatoa en 1883 aurait généré une énergie comparable à 13.000 Little Boy, soit une énergie comparable à l'énergie sismique d'un séisme de magnitude 8,3.

Autre comparaison. L'énergie consommée en France chaque année (E_F) est de l'ordre de 274,6 Mtep soit 1,15 10¹⁹ J. Ce qui donne log₁₀(E_F) = 19,06, soit l'équivalent de l'énergie sismique libérée lors d'un séisme de magnitude 9,8. L'énergie consommée en France en 1 an représente donc plus de 30 fois l'énergie sismique libérée par le puissant séisme du Chili du 27 février 2010, et même environ 2,8 fois l'énergie sismique libérée par le séisme "record" de 1960.