L'histoire de l'âge de la Terre

Suivant leurs différentes croyances, les Hommes se préoccupaient ou non de l'origine de la Terre. Et il y avait autant de récits de cette « création » que de peuples s'y intéressant. Pour les anciens Égyptiens, la Terre est née (on ne sait pas trop comment) du Noun, un “monde” inerte, un chaos, sans terre, sans vie, sans mort, sans jour ni nuit, sans aucune espèce vivante. C'était une grande étendue d'eau, l'Océan primordial. Pour les Grecs archaïques, la Terre (Gaïa) était née à partir du désordre (Chaos), à un âge non précisé, alors que pour de nombreux philosophes de la Grèce classique (Aristote…), la Terre avait toujours existé. Le bouddhisme ne s'intéresse pas à l'origine du monde, mais à son évolution. Pour les trois religions monothéistes, (par ordre chronologique d'apparition, judaïsme, christianisme, et islam), il y a un même récit de la création de la Terre, des astres et de la vie par un Dieu préexistant. La Création dura 6 jours. Dieu créa d'abord le ciel, la Terre et la lumière (1^er jour), ensuite il sépara les eaux et le ciel (2^e jour), puis il forma la mer, les terres émergées, et les plantes (3^e jour), puis le Soleil, la Lune et les étoiles (4^e jour), puis les oiseaux et les animaux marins (5^e jour), et il termina par les reptiles, les mammifères et enfin l'Homme (6^e jour). Il se reposa le 7^e jour. Beaucoup de ces éléments se retrouvent dans des récits sumériens antérieurs à l'écriture de la Bible.

Avant de se demander quand a eu lieu cette semaine extraordinaire, on peut, comme le recommandent les programmes de lycée, chercher dans l'art comment les artistes ont représenté cette création de la Terre. Les artistes (peintres, enlumineurs…) ont abondamment représenté la création de l'Homme, un peu moins celles des plantes et des animaux, et très peu les créations “géologiques” ou “astronomiques”. Par exemple, les ultra-célèbres fresques de la Chapelle Sixtine (peintes par Michel-Ange au début du XVI^e siècle entre 1508 et 1512) représentent la création d'Adam que tout le monde connait et où Dieu touche le doigt d'Adam. Moins connues mais toujours dans la Chapelle Sixtine, Michel-Ange a aussi peint la création du Soleil et de la Lune ; mais rien sur la création de la Terre. Il faut rechercher dans des œuvres des siècles précédents pour retrouver des représentations de la création de la Terre. Citons-en deux : un Dieu architecte dans une Bible moralisée du XIII^e siècle (auteur anonyme), œuvre conservée à la Bibliothèque nationale autrichienne de Vienne, et une Création du Monde, datant de 1445, peinte par Giovanni di Paolo (1398-1482) et conservée au Metropolitan Museum of Art (MET) de New York. Ces deux représentations sont symboliques, et ne cherchent pas à expliquer comment Dieu s'y est pris pour créer la Terre.

Source - © 1220-1230 Anonyme / Österreichische Nationalbibliothek Figure 1. La Création du Monde dans la Bible moralisée (codex 2554) de Vienne, livre enluminé datant de la première moitié du XIIIe siècle On y voit un Dieu architecte avec un compas (on est dans le siècle des bâtisseurs de cathédrales). On y reconnait la Terre au centre, Le Soleil, la Lune et les étoiles, et l'eau au-dessus des cieux.

Source - © 1445 Giovanni di Paolo / Metropolitan Museum of Art, New York Figure 2. La Création du Monde de Giovanni di Paolo (milieu 15e siècle)

Source - © 1508-1512 Michel-Ange / kerdonis.fr Figure 3. La création du Soleil et de la Lune par Michel-Ange (début du XVIe siècle)

Comment dater cette création de la Terre, des astres, de la vie et de l'Homme avec seulement ces livres sacrés ? L'interprétation à la lettre de ces textes, sources des illustrations ci-dessus, permet de calculer l'âge de la Terre, car ces récits donnent l'âge des personnages de cette histoire. D'après ces textes, Noé, par exemple, vécut 950 ans, Mathusalem 969 ans, Abraham 175 ans… On vivait vieux à l'époque ! Il suffit alors, si l'on interprète ces chiffres à la lettre, de faire une addition, puis de recaler ces âges bibliques avec les calendriers romain puis julien pour avoir la date de la création du Monde. Par exemple, l'évêque irlandais Ussher (1581-1656) calcula que Dieu commença la Création au début de la nuit du 22 octobre de l'an 4004 av. J.-C. ! D'autres chronologies moins caricaturales furent proposées sur de telles bases religieuses, et toutes donnaient des âges de quelques milliers d'années.

Mais les géologues, dès le XVII^e siècle, avaient du mal avec ces courtes durées. Comment expliquer en quelques milliers d'années la formation de profondes vallées, de hautes montagnes… ? L'intervention du Déluge, commode, n'expliquait pas tout.

On peut noter que l'interprétation à la lettre de ces textes conduit à la fois à une Terre très jeune et au créationnisme. En 2011, une étude faite par Ipsos et l'agence Reuter (évoquée dans la page Créationnisme) donnait des chiffres concernant le pourcentage de la population croyant au créationnisme dans différents pays. On peut supposer que la fréquence des partisans d'une Terre très jeune est du même ordre de grandeur. Citons ces pourcentages pour quelques pays, dans l'ordre décroissant : l'Arabie saoudite (75 %), le Brésil (47 %), les USA (40 %), l'Inde (33 %), la Pologne (25 %), le Japon, la Chine et la majorité des pays Ouest-européens dont la France (autour de 10 %). Ce “classement” traduit un combiné de (1) l'importance de l'influence des plus rétrogrades des religieux, et (2) de la qualité de l'enseignement public. Les professeurs de science, de SVT en particulier, ont donc encore un rôle important à jouer, même en France (10 %, c'est beaucoup) !

À partir du XVIII^e siècle, les scientifiques commencèrent à séparer science et religion. Buffon (1707-1788) publia discrètement (dans le tome 1 des Suppléments à l'Histoire Naturelle, 1774) un mémoire intitulé Expériences sur les progrès de la chaleur dans les corps. En quelques pages, il décrit des expériences faites sur le refroidissement de boulets de canon chauffés dans une forge. Pourquoi Buffon a-t-il étudié le refroidissement de boulets ? Parce qu'il pensait que Terre et planètes étaient des morceaux du Soleil qui en avaient été arrachés par la collision avec une comète. La Terre avait donc eu une origine très chaude. Il extrapola à la Terre les résultats obtenus sur ces petites sphères. Il obtint plusieurs résultats, les extrapolations variant selon le choix de certaines hypothèses. Il a choisi de publier le plus petit des âges calculés, 96 670 ans, quand même 16 fois plus grand que les âges bibliques. Et il n'a pas du tout exploité ce chiffre dans la suite de son œuvre. Dans un pays et à une époque où la religion était puissante, on n'était jamais trop prudent ! On peut lire des extraits des travaux de Buffon et des commentaires à leur sujet dans Buffon, ou comment le siècle des Lumières envisageait l'origine du monde.

Source - © 1749 in Buffon – Photo Pierre Thomas

Figure 4. L'origine de la Terre, extrait de l'œuvre de Buffon (1749)

Buffon proposait que la Terre soit un fragment du Soleil arraché par le passage d'une comète ; c'est pour cela qu'il a supposé une Terre initiale à haute température et qu'il a étudié la vitesse de refroidissement de boulets pour évaluer l'âge de la Terre. On peut noter que Buffon a dessiné un Dieu ressemblant beaucoup au Dieu créant Adam de Michel-Ange (Chapelle Sixtine). Mais dans le dessin illustrant le livre de Buffon, Dieu ne touche rien, n'intervient pas, mais est présent, surveille… Dessiner Dieu était une mesure de prudence sous Louis XV (rappelons-nous la triste fin du chevalier de la Barre).

Illustration issue de Buffon, 1749. Histoire naturelle, générale et particulière, Tome premier, chapitre Preuves de la théorie de la Terre, p.185

Durant la fin du XVIII^e et tout le XIX^e siècle, il y eut deux types d'approches pour dater la Terre : l'approche géologique qui restait semi-quantitative à l'époque, et l'approche physique plus quantitative et appliquant les lois de la physique naissante. Les géologues voyaient des montagnes et leur érosion, le remplissage des mers anciennes par des sédiments. Il était très difficile à ces époques de mesurer une moyenne des vitesses d'érosion et de sédimentation, extrêmement variables. Ce qui était sûr, c'est que ces vitesses étaient très faibles. Par exemple, les vallées du Rhône et de son affluent le Gard ne s'étaient pas approfondies significativement entre l'époque romaine et le XIX^e siècle, comme l'attestent les ruines de ponts romains qu'on y trouve. Pour que l'“énormité” de l'érosion ou de la sédimentation constatées ait eu lieu, il fallait des centaines de millions d'années.

Source - © 1851 Édouard Baldus Figure 5. Le Pont du Gard photographié en 1851, soit environ 18 siècles après sa construction par les Romains L'absence d'érosion mesurable pendant ces 18 siècles montrait l'extrême lenteur des phénomènes géologiques aux géologues du XIXe siècle.

Source - © 1784 in Palassou – Photo Pierre Thomas Figure 6. Vallées des Pyrénées, gravure extraite d'un livre du géologue Pierre Bernard Palassou (1745–1830) L'épaisseur des couches sédimentaires, leurs plissements, la profondeur des vallées… tout cela impliquait un temps très long pour la formation et l'érosion des Pyrénées. Illustration issue de Pierre Bernard Palassou, 1784. Essai sur la Minéralogie des Monts-Pyrénées

De même, l'étude des fossiles, de leur variation dans la succession des strates et leur comparaison avec les êtres vivants actuels montraient que les êtres vivants évoluaient au cours du temps. Et comme l'évolution est insensible sur plusieurs millénaires (comme le montre la comparaison entre les animaux actuels et les animaux momifiés par les Égyptiens, cf. L'évolution est un phénomène lent), il fallait des centaines de millions d'années pour “transformer” les animaux anciens en animaux actuels.

Source - © 2015 Richard Carter, The great Darwin fossil hunt

Figure 7. Planche 3 du livre de Darwin (1809-1882) Geological Observations on South America (1846), livre décrivant des fossiles collectés en Amérique du Sud lors de son tour du monde à bord du Beagle (1831-1836)

Ce sont, entre autres, les observations faites au cours de ce voyage qui ont permis à Darwin non pas de démontrer l'Évolution (il n'y avait plus de doute chez les vrais naturalistes du milieu du XIX^e), mais d'en proposer un mécanisme.

Tous ces raisonnements étaient basés sur le principe que la nature actuelle obéissait aux mêmes règles que la nature passée, principe clairement énoncé par Charles Lyell (1797-1875) dans les années 1830-1835. Mais quelques autres naturalistes (dont George Cuvier, 1769-1832) expliquaient les mêmes observations (érosion, sédimentation…) avec des temps plus courts en faisant appel à des « catastrophes », des « déluges », brèves périodes avec érosion, sédimentation et évolution très rapides.

Le défaut de ces approches naturalistes, c'était d'être relativement empiriques, et non fondées (à l'époque) sur des mesures précises et sur des lois physiques, biochimiques… bien établies.

L'utilisation des lois de la propagation de la chaleur bien connues dans la deuxième moitié du XIX^e siècle (les lois de Fourier datent de 1822) ont permis à lord Kelvin (1824-1907) de reprendre les idées de Buffon sur le refroidissement de la Terre, non pas expérimentalement, mais en calculant le temps nécessaire à une Terre pour passer de l'état d'une boule de magma à la Terre actuelle avec son degré géothermique superficiel de 30 K/km. Après plusieurs valeurs proposées, un consensus autour de 20 à 40 Ma s'établit dans la communauté des physiciens des années 1890.

Source - © 2014 Pierre Thomas

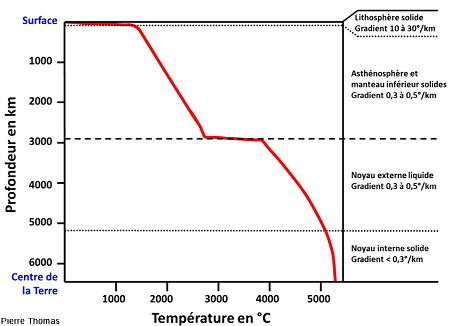
Figure 8. Évolution de la température interne de la Terre en fonction de la profondeur

La température n'augmente très fortement avec la profondeur que dans deux zones restreintes : la lithosphère superficielle (d'épaisseur comprise entre 0 et 150 km) et de part et d'autre de la limite manteau/noyau (vers 2900 km de profondeur). Ces deux zones correspondent à ce que les physiciens appellent des « couches limites thermiques », minces couches situées au sommet et à la base des cellules de convection terrestre pour lesquelles la variation de température avec la profondeur est très faible, et égale au gradient adiabatique (ou plus précisément isentropique).

Au XIX^e on ne mesurait le gradient thermique qu'en surface (~30K/km) et peu de physiciens envisageaient la possible convection de l'intérieur de la Terre. De plus la production de chaleur interne par radioactivité ne fut envisagée qu'à partir du début du XX^e siècle.

Figure à retrouver dans La chaleur de la Terre et la géothermie.

Les astronomes de la fin du XIX^e siècle proposaient que le Soleil tire son énergie de sa contraction. Un rapide calcul de perte d'énergie potentielle d'un corps « très grand » (idéalement infini) ayant la masse du Soleil (1,9891.10³⁰ kg), se contractant en rayonnant sa puissance actuelle (luminosité, J de 4.10²⁶ W) pour atteindre sa taille actuelle (diamètre de 1 392 684 km) prouvait que cette contraction durait depuis largement moins que 100 Ma. Pour cela, il suffit d'appliquer la formule d'Helmholtz (1821-1894) : τ= E/L, τ étant le temps caractéristique pendant lequel l'étoile peut rayonner une puissance L avec une énergie totale libérable E= G.M²/ 2R, avec G la constante de gravitation universelle, M et R les masse et rayon du Soleil.

Et, en cette fin du XIX^e siècle, John Joly (1857-1933) reprit les idées d'Edmond Halley (1656-1752, celui qui a découvert la périodicité de la comète qui porte désormais son nom). Ce dernier proposait que l'océan primitif était constitué d'eau douce. Cet océan reçoit par les fleuves de l'eau très légèrement salée, alors qu'il perd par évaporation de l'eau parfaitement douce. Halley pensa (sans pouvoir le faire) que si on connaissait la faible salinité moyenne des fleuves, leur débit total, et le volume total des océans, il serait facile de calculer combien de temps il aurait fallu à ces fleuves pour amener à la mer tout le sel qui s'y trouve. Deux siècles plus tard, Joly connaissait les valeurs de la salinité de la mer et des fleuves, le volume de la mer, la somme des débits des grands fleuves, et put faire les calculs en négligeant la précipitation des évaporites, roches somme toute assez rares (dépôts issus de la concentration d'eaux douces ou marines par évaporation et aboutissant à la précipitation de sels). Il trouva un âge de la Terre (ou plus précisément des océans) d'environ 80 Ma.

Les géologues demandaient plusieurs centaines de millions d'années pour expliquer leurs observations, les physiciens en proposaient quelques dizaines pour expliquer leurs mesures et leurs calculs. La physique nucléaire débutant au tout début du XX^e siècle et la découverte des dorsales dans la deuxième moitié du XX^e siècle donnèrent raison aux géologues et expliquèrent pourquoi les physiciens de l'époque avaient eu tort.

Figure 9. Portraits de quatre des acteurs de la querelle entre une Terre à histoire longue et une Terre à histoire courte

Lyell et Darwin (en haut) proposaient une histoire “longue” sur la base d'observations et de mesures géologiques, alors que Kelvin et Joly proposaient une histoire “courte” sur la base de mesures et de modèles physiques (modèles qui, plus tard, se sont avérés incomplets).

La radioactivité fut découverte en 1896. On a alors rapidement montré qu'un isotope radioactif P (P comme “père”) se transforme en un isotope radiogénique F (F comme “fils”), et ce avec une loi connue :

avec λ la constate radioactive caractéristique de chaque noyau radioactif, P la quantité d'élément père mesurée aujourd'hui dans l'échantillon considéré, P₀ la quantité initiale de père dans l'échantillon, et t l'âge de l'échantillon.

On a une équation unique et deux inconnues (P₀ et t) : ce qui ne se résout pas. On peut prendre le fils, en écrivant que :

F représentant la quantité d'élément fils mesurée aujourd'hui dans l'échantillon, F₀ la quantité initiale d'élément fils dans l'échantillon, et (P₀−P) la quantité d'élément père qui s'est désintégrée.

En reportant l'équation 2 dans l'équation 1, on arrive à :

Encore une équation à deux inconnues (F₀ et t), ce qui ne se résout toujours pas !

Dans certains cas particuliers, P₀ ou F₀ sont connus. Citons-en trois. Dans le cas de la méthode de datation au ¹⁴C, ¹⁴C₀ est constant et (approximativement) égal à la concentration en ¹⁴C de l'atmosphère (anté-industrielle et anté-nucléaire). P₀ est donc connu. Pour la datation potassium-argon (K-Ar) et dans les minéraux riches en potassium (comme l'orthose [KAlSi₃O₈], les micas blancs…), on peut considérer que ⁴⁰Ar₀ est négligeable devant le ⁴⁰Ar radiogénique. Dans certains types de minerais d'uranium et de thorium, le Pb₀ et/ou le He₀ sont négligeables devant le Pb et l'He radiogéniques. Dans ces deux derniers cas, F₀ est connu car supposé nul. Donc, sauf pour de tels cas particuliers (rares et ne permettant pas de dater la formation de la Terre), on ne peut pas dater un échantillon unique.

Il existe de nombreux couples P-F dont un des plus utilisés est le couple ⁸⁷Rb-⁸⁷Sr que nous prendrons comme exemple. L'équation 3 s'écrit alors ⁸⁷Sr = ⁸⁷Sr₀ + ⁸⁷Rb.(e^λt− 1), bien sûr toujours impossible à résoudre puisqu'il y a toujours deux inconnues, t et ⁸⁷Sr₀ . Mais, à côté du ⁸⁷Sr pour partie radiogénique, pour partie déjà présent dans l'échantillon au temps t=0, il existe un strontium ni radioactif ni radiogénique, ⁸⁶Sr, dont la quantité, bien que variable d'un échantillon à l'autre en fonction de la teneur de l'échantillon en strontium, est constante dans le temps dans un échantillon donné. On peut donc écrire pour un échantillon ⁸⁶Sr = ⁸⁶Sr₀.

Or, un processus géologique peut former plusieurs “échantillons” à partir d'un même milieu, par exemple plusieurs minéraux à partir d'un même magma, des roches différentes par différenciation dans un même réservoir magmatique… Les échantillons nés d'un même milieu sont dits cogénétiques. Ces échantillons cogénétiques peuvent être chimiquement différents. Le rubidium étant un métal alcalin (monovalent, comme Na et K) et le strontium un alcalinoterreux (divalent, comme Mg et Ca), des échantillons par exemple riches en orthose [KAlSi₃O₈] seront riches en rubidium et pauvre en strontium, et inversement pour des échantillons riches en amphibole [par exemple, en actinote Ca₂(Mg,Fe)₅Si₈O₂₂(OH)₂]. Ils sont chimiquement différents certes, mais isotopiquement identiques au temps 0. En effet, les processus géologiques ne séparent pas les isotopes d'un même élément si ceux-ci sont suffisamment “lourds” pour que leur différence de masse soit négligeable par rapport à leur masse moyenne. Donc, quand un processus géologique fabrique des roches (ou des minéraux) différents au même moment à partir d'un même milieu, les isotopes du strontium ne sont pas séparés. Le rapport (⁸⁷Sr/⁸⁶Sr)₀ du milieu de genèse est inconnu, variable d'un milieu à un autre, mais est identique pour tous les échantillons formés à partir de ce même milieu au même moment. On reprend alors l'équation 3 et on divise les deux membres par une valeur constante, à savoir ⁸⁶Sr de l'échantillon (qui est égal à ⁸⁶Sr₀). Cela nous donne :

Cette équation a toujours 2 inconnues, ⁸⁷Sr₀/⁸⁶Sr₀ et t, et diviser les deux membres d'une équation à deux inconnues par une même quantité ne permet toujours pas de la résoudre. Mais si on prend 2 échantillons contemporains et cogénétiques, on aura deux équations (une par échantillon) mais avec seulement deux inconnues, t, que l'on cherche, et le rapport ⁸⁷Sr₀/⁸⁶Sr_0, inconnu mais identique dans les deux échantillons puisque, rappelons-le, les processus géologiques ne séparent pas les isotopes lourds. Et un système de 2 équations à 2 inconnues se résout !

La suite est une histoire de “cuisine mathématique.” On peut résoudre graphiquement un système de n équations à 2 inconnues si n≥ 2.

L‘équation 4,

est de la forme

Si on prend n échantillons contemporains et cogénétiques, qu'on en analyse les quantités ⁸⁷Sr, ⁸⁶Sr et ⁸⁷Rb, et qu'on reporte ces analyses dans un diagramme ⁸⁷Sr/⁸⁶Sr (Y) fonction de ⁸⁷Rb/⁸⁶Sr (X), ces n points seront théoriquement alignés sur une droite de pente e^λt− 1 (a). Cette droite est appelée “isochrone” et sa pente permet de calculer t. Si les points sont alignés, à moins d'un hasard totalement improbable si n est grand, c'est qu'ils sont contemporains, cogénétiques et d'âge donné par la pente. Si les échantillons sont non contemporains ou non cogénétiques, alors les points analytiques ne s'aligneront pas sur une droite.

Et dès le début du XX^e siècle, d'abord avec des méthodes où F₀ était connu, on a pu dater des échantillons de roches d'âge supérieur à 2 milliards d'années^[2], en particulier des minerais d'uranium et des granites. Les chronologies courtes étaient donc fausses.

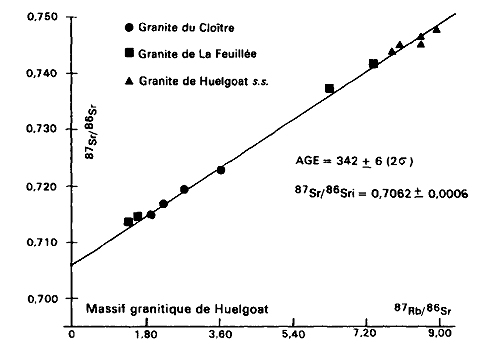
Source - © 1988 Notice de la carte géologique de Huelgoat

Figure 10. Exemple d'une droite isochrone obtenue avec la méthode Rb–Sr, celle du complexe granitique de Huelgoat, en Bretagne

Ce complexe granitique est en fait composé de trois granites différents, eux-mêmes chimiquement et minéralogiquement légèrement variables : les granites de La Feuillée, du Cloitre et de Huelgoat sensu stricto. Des arguments géologiques indiquent que ces trois granites sont cogénétiques et contemporains. L'analyse de 13 échantillons pris dans ces 3 granites montre qu'ils sont alignés sur une droite dans un diagramme ⁸⁷Sr/⁸⁶Sr fonction de ⁸⁷Rb/⁸⁶Sr. Cet alignement (1) confirme que ces trois granites sont contemporains et cogénétiques, ce qu'indiquaient déjà des études géologiques, (2) permet de calculer la pente de cette droite (égale à e^λt− 1), ce qui donne un âge de 342 ± 6 Ma. Les granites bretons sont effectivement plus vieux que les 100 Ma maximum que donnaient à la Terre les physiciens du XIX^e siècle.

Il existe beaucoup d'autres chronomètres que le couple rubidium-strontium, dont les deux chronomètres ²³⁵U-²⁰⁷Pb et ²³⁸U-²⁰⁶Pb, chronomètres que l'on peut combiner en une méthode combinée dite Pb-Pb. On trace alors des droites isochrones dans un diagramme ²⁰⁷Pb/²⁰⁴Pb en fonction de ²⁰⁶Pb/²⁰⁴Pb, le ²⁰⁴Pb n'étant ni radioactif ni radiogénique (il “joue le rôle” du ⁸⁶Sr dans la méthode Rb-Sr). L'âge est donné par la pente, qui, dans cette méthode Pb-Pb est égale à [²³⁵U/²³⁸U.(e^λ₂₃₅t– 1)/(e^λ₂₃₈t– 1)].

En choisissant parmi toutes ces méthodes basées sur la radioactivité, on peut, selon les cas et les méthodes employées, dater des minéraux isolés, des roches magmatiques ou métamorphiques (mais hélas beaucoup plus rarement des roches sédimentaires). La roche la plus vieille connue à ce jour a environ 4,2 Ga. C'est une roche volcanique (métamorphisée) qui provient du Québec (Nuvvuagittuq Greenstone Belt). Cette datation est encore sujette à des débats scientifiques et méthodologiques. Le plus vieux minéral connu est un zircon (ZrSiO₄) australien (Jack Hills) daté de 4,4 Ga. La Terre est donc plus vieille que 4,4 Ga. Mais comment dater la Terre globale, et non pas telle roche, tel minéral, telle formation géologique… ?

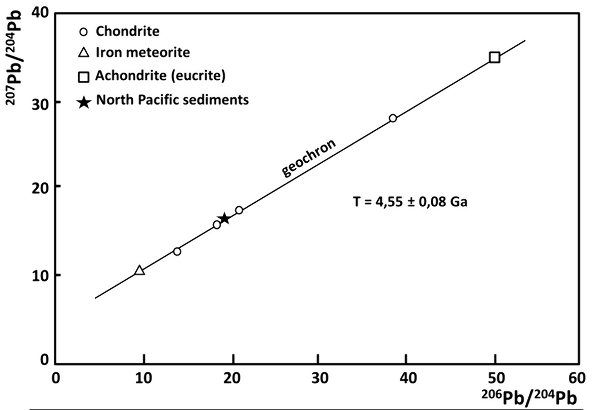
C'est le chronomètre Pb-Pb qui a donné le premier âge précis pour la Terre. En 1953, Clair Patterson (1922-1995) entreprit de dater les météorites. En prenant plusieurs minéraux dans une même météorite, il trouva une isochrone donnant un âge de 4,5 Ga. En analysant globalement plusieurs types de météorites chimiquement et minéralogiquement différentes (chondrites, achondrites, météorites de fer…), il trouva aussi un âge de 4,5 Ga. Outre l'intérêt de connaitre l'âge des météorites, cela prouvait (à moins d'un malencontreux hasard hautement improbable) que toutes les météorites étaient contemporaines et cogénétiques. Tous les objets du système solaire qu'on pouvait analyser à l'époque (les météorites provenant de la ceinture des astéroïdes) étaient contemporains et cogénétiques. Or, le système solaire forme un ensemble cohérent : tous ses corps, astéroïdes compris, sont dans un même plan, tournent dans le sens qui est aussi le sens de rotation du Soleil sur lui-même… Il n'est pas illogique de penser que l'ensemble des corps du système solaire, Terre comprise, soient contemporains et cogénétiques. Il ne reste plus qu'à le confirmer ou l'infirmer. Mais quel(s) échantillon(s) prendre pour dater la Terre entière ? Il fallait trouver un (des) échantillon(s) terrestre(s) dont le plomb soit représentatif du plomb de toute la Terre et non pas de telle ou telle formation géologique. Patterson s'est dit que le peu de plomb contenu dans les sédiments des plaines abyssales océaniques moyennait sans doute les isotopes du plomb dissout dans l'eau de mer qui, lui-même, moyennait les plombs provenant des continents, des basaltes océaniques, du manteau… Il a donc supposé que ce plomb océanique était isotopiquement représentatif du plomb des silicates de la Terre. Et, après analyse, le plomb de ces sédiments océaniques se place parfaitement sur l'isochrone des météorites, ce résultat fut publié en 1956. Cela prouve, à moins d'un hasard hautement improbable, que Terre (en toute rigueur ses silicates) et météorites sont contemporaines et cogénétiques, et ont ce même âge de 4,5 Ga, qui est l'âge du système solaire. Cet âge a été confirmé et précisé depuis 1956 par beaucoup d'autres méthodes basées sur la radioactivité.

Source - © 1962 D'après Murthy et Patterson, redessiné

Figure 11. Exemple d'une droite isochrone (geochron en anglais) pour déterminer l'âqe de la Terre, publiée par Clair Patterson, republiée 6 ans plus tard dans un article de Murthy et Patterson (1962), et redessinée pour cet article

Articles sources.

C.C. Patterson, 1956. Age of meteorites and the earth, Geochimica et Cosmochimica Acta, 10, 4, 230-237 [pdf]

V.R. Murthy, C.C. Patterson, 1962. Primary isochron of zero age for meteorites and the Earth, Journal of Geophysical Research, 67, 3, 1161-1167

On peut alors se demander pourquoi les physiciens du XIX^e siècle s'étaient autant trompés. Parce que leurs modèles étaient très incomplets. Joly ne connaissait pas les dorsales et ne savait pas que leur volcanisme sous-marin absorbe le sodium de la mer (cf. Un volcanisme bien méconnu et pourtant si riche d'enseignement : le volcanisme du Crétacé supérieur du Pays Basque, ses pillow-lavas et la salinité de l'eau de mer). Les astronomes ne connaissaient pas la fusion de l'hydrogène en hélium, source de l'énergie du Soleil qui ne fut proposée qu'en 1919. Kelvin ne connaissait pas la radioactivité, source de chaleur qui limite le refroidissement de la Terre. On ne peut pas reprocher ces “ignorances” à ces scientifiques du XIX^e siècle. On peut par contre leur reprocher de ne pas avoir discuté avec les géologues pour juger de la pertinence de leurs observations et de leurs idées. Mais ce n'étaient pas quelques « ramasseurs de cailloux » qui allaient mettre en doute la physique classique qui montrait chaque jour sa toute-puissance. On peut aussi reprocher à Kelvin d'avoir négligé les diverses possibilités de convection (à l'état solide, liquide, mixte) internes à la Terre, ce dont a tenu compte en 1895 l'un de ses élèves, Perry, ce qui, dans de nombreux cas, donnait un âge plus grand. Mais on ne l'a que très peu écouté à l'époque. Allait-on écouter un « jeune homme » qui osait contredire le « grand » Kelvin ?

Une fois l'âge de la Terre connu, il reste deux grandes questions : la Terre est “née” il y a 4,5 Ga, mais à partir de quoi, et comment ? Mais c'est une autre histoire.