Article | 19/01/2017
Les oppositions des planètes, observations autour des oppositions de Jupiter et Saturne en 2017
19/01/2017
Résumé
À partir de l'exemple des planètes Jupiter et Saturne, explication des observations que l'on peut faire autour de leurs oppositions par la disposition de ces planètes et de la Terre dans le système solaire. Sont abordés les transits de satellites de Jupiter, les saisons de Saturne, et la parallaxe planétaire ou stellaire (parsec).
Table des matières
Le printemps 2017 est pour les 2 planètes géantes, Jupiter et Saturne, le moment de leur passage à l'opposition (avril pour Jupiter, juin pour Saturne). L'opposition est la position dans laquelle la Terre se trouve alignée entre le Soleil et un objet (planète, astéroïde, comète) dont l'orbite autour du Soleil est externe à celle de la Terre. C'est aussi le moment où ces planètes sont les plus lumineuses (à l'œil nu), les plus grosses (à la lunette ou au télescope), et sont visibles tout au long de la nuit, comme peut l'être la pleine lune (la pleine lune n'étant autre, géométriquement, que l'opposition de la Lune).
Géométrie de l'opposition – Exemple de Jupiter
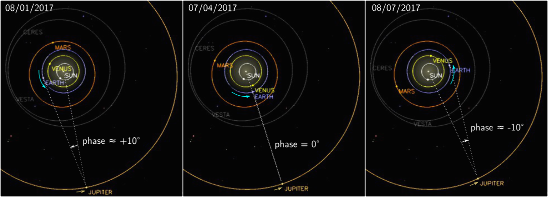
Lors de son opposition, Jupiter nous parait éclairée pleinement, contrairement aux autres périodes de l'année, même si, en pratique, l'aspect de la planète dans un télescope ne change quasiment pas. En effet, l'angle maximal Soleil-Jupiter-Terre, qu'on appelle l'angle de phase de Jupiter, n'atteint au maximum que 10° environ (Figure 1). En conséquence, le disque de Jupiter n'apparait jamais moins éclairé qu'à 99% depuis la Terre : on distingue donc à peine un bord un peu plus sombre que l'autre, et on ne voit jamais un croissant de Jupiter ! C'est la même chose pour toutes les planètes extérieures : l'angle de phase maximal de Mars, plus proche du Soleil, est de l'ordre de 45° (le disque de Mars apparaît alors éclairé à 85%) ; celui de Saturne, plus éloignée du Soleil, d'un peu moins de 6° (le disque de Saturne apparaît toujours éclairé à plus de 99%).
La situation est par contre totalement différente pour les planètes intérieures à l'orbite de la Terre (Vénus et Mercure) pour lesquelles des phases sont visibles depuis la Terre, de presque 0° (éclairées à 100%, quand elles sont derrière le Soleil) à 180° (en transit devant le Soleil). L'observation de ces phases des planètes intérieures par Galilée a été un argument en faveur du système héliocentrique copernicien.
Source - © 2017 D'après simulations Solar System Simulator (Caltech/JPL)
On a repéré en pointillés les directions Soleil-Jupiter et Terre-Jupiter et indiqué la valeur approximative de l'angle de phase Soleil-Jupiter-Terre. Minimal à l'opposition (0° le 7/04), il est maximal environ 3 mois avant ou après (10° les 8/01 et 8/07). Des flèches courbées le long des orbites de la Terre et de Jupiter symbolisent le sens et la valeur relative de leur mouvement orbital.
Le changement de phase de Jupiter ou Saturne n'est pas décelable à l'oculaire d'un petit télescope sur le disque de ces planètes. En revanche, pour Jupiter, l'angle de phase variable est mis en évidence par les transits de ses satellites et de leurs ombres sur la planète. Lors de l'opposition, les satellites et leurs ombres sont parfaitement superposés sur Jupiter (Figure 2) alors qu'avant l'opposition, les ombres précèdent les satellites sur la planète (Figure 3), et qu'après l'opposition, les ombres suivent les satellites (Figure 4). Des simulations du système de Jupiter en perspective (Figure 5), aux mêmes dates, permettent de visualiser ce changement de disposition géométrique.
Source - © 2017 D'après simulations Stellarium Remarquer la superposition parfaite entre Ganymède et son ombre sur le disque de Jupiter. | |
Source - © 2017 D'après simulations Stellarium Remarquer le décalage, « en avance », de l'ombre d'Io par rapport au satellite, qu'on peut estimer à presque 1 rayon de Jupiter. Ce décalage est dû au fait que le Soleil n'est pas directement « dans notre dos », mais légèrement sur la gauche (voir schéma ci-dessous). | Source - © 2017 D'après simulations Stellarium Remarquer le décalage, « en retard » cette fois, de l'ombre d'Europe par rapport au satellite, qu'on peut estimer à 1 rayon de Jupiter et deux tiers (5/3 donc). Ce décalage, inverse du cas précédent, est dû au fait que le Soleil n'est pas directement « dans notre dos », mais légèrement sur la droite (voir schéma ci-dessous). |
Source - © 2017 D'après simulations Celestia La ligne de visée Terre-Jupiter correspond à la verticale. Des flèches rouges le long des orbites des satellites indiquent le sens de leur mouvement orbital. La direction Soleil-Jupiter est indiquée par une flèche jaune pointant, depuis Jupiter, en direction du Soleil. L'angle φ (entre les lignes en pointillés blancs) est l'angle de phase Soleil-Jupiter-Terre. Remarquer l'écart, noté par la cote" s", entre les lignes de visée (depuis la Terre) menant au satellite de Jupiter ou à son ombre, avant et après l'opposition. | |
Les transits des satellites de Jupiter et de leurs ombres permettent donc de savoir si l'on observe avant ou après l'opposition. Mieux, on peut retrouver l'angle de phase φ Soleil-Jupiter-Terre en appliquant une relation trigonométrique. En effet, on connaît les rayons des orbites d'Io et Europe par rapport au centre de Jupiter (c'est leur élongation maximale au cours de leur révolution), respectivement 6 et 9,6 rayons de Jupiter (RJ). On considère ensuite que le plan image des ombres projetées sur Jupiter est à 1 RJ du centre de la planète (c'est à peu près le cas quand l'ombre est proche du milieu de son transit). Dans l'exemple de la figure 3 ci-dessus, il y a une séparation apparente s ≈ 1 RJ entre Io et son ombre sur Jupiter, et la distance D vraie entre Io et cette ombre vaut donc D = 6 – 1 = 5 RJ. Les angles étant petits, on a alors de manière approchée : φ ≈ sinφ ≈ s / D ≈ 1/5 = 0,2 radian, soit φ≈ 11°. Dans le cas de la figure 4, en gardant les mêmes notations, on a cette fois : s ≈ 5/3 RJ et D = 9,6 – 1 = 8,6, d'où φ ≈ sinφ ≈ s / D ≈ (5/3) / 8.6 = 0,19 radian, soit φ≈ 11° également. On retrouve bien les valeurs d'angles de phase donnés par les simulations. Un petit exercice d'application de trigonométrie à proposer aux collègues de mathématiques ?
Pour suivre cette évolution, vous pouvez prévoir d'observer des transits de Jupiter, grâce à une lunette ou un télescope, au cours du premier semestre 2017. Les transits de satellites de Jupiter ont lieu assez fréquemment, mais pas toutes les nuits non plus... Pour savoir si lors d'une nuit d'observation vous pourrez voir des transits des satellites de Jupiter, voici quelques possibilités :
- utiliser le logiciel Stellarium, en zoomant sur Jupiter et en faisant défiler le temps ;
- consulter une liste de tous les transits calculée à partir des éphémérides de l'IMCCE, comme celle mise en ligne sur le site PGJ astronomie (colonne de droite pour la France métropolitaine seulement) ;
- utiliser l'almanach interactif (utilisant les mêmes éphémérides) mis en ligne sur le site du magazine américain Sky&Telescope à la page dédiée à l'observation des satellites de Jupiter, après s'être enregistré sur le site (il suffit de donner un pseudo et un email).
Géométrie de l'opposition de Saturne
Saturne passe à l'opposition le 15 juin 2017 vers midi en France métropolitaine, avec son rapprochement maximal annuel à minuit la nuit suivante (à 9,04 UA de la Terre, UA pour Unité Astronomique – la distance moyenne Terre-Soleil soit ~150 millions de km). La brillance de Saturne sera alors maximale avec une magnitude de 0, la même que celle de l'étoile Véga, qui est par définition la référence 0 de l'échelle des magnitudes (Vega est derrière Sirius la plus brillante des étoiles visibles depuis la France métropolitaine, au coude à coude avec Arcturus). Notons que la luminosité de Saturne (vue depuis la Terre) varie assez peu sur une année car Saturne orbitant loin du Soleil (entre 9 et 10 UA), la révolution de la Terre autour du Soleil (à 1 UA) n'augmente et ne réduit cette distance que d'environ 10%. Il en résulte que la magnitude de Saturne varie de 0,5 unité seulement autour de chaque opposition.
En revanche, d'une opposition à l'autre, la luminosité de Saturne varie par la combinaison de deux facteurs : la distance de Saturne au Soleil (qui varie de 1 UA), et, surtout, la surface apparente des anneaux autour de la planète, surface qui change lentement avec la révolution de Saturne autour du Soleil. En effet, comme celui de la Terre, l'axe de rotation de Saturne (et de son système d'anneaux et de satellites) présente une obliquité non nulle, c'est-à-dire qu'il est incliné par rapport au plan de son orbite, d'environ 26,7° (23,4° pour la Terre). En raison de cette obliquité semblable, Saturne connait des saisons à la géométrie comparable aux saisons terrestres (mais en 29 fois plus lent, du fait de la durée de l'"année de Saturne").
Au cours des saisons, l'angle entre le plan des anneaux de Saturne et la ligne de visée Terre-Saturne évolue. À l'équinoxe de Saturne, les anneaux nous montrent leur tranche et sont quasiment invisibles ; aux solstices, les anneaux sont par contre penchés vers la Terre de près de 27° et montrent une surface maximale (cf. Jeux d'ombres sur Saturne, ses anneaux et ses satellites pendant l'équinoxe de 2009). Or le solstice de l'été Nord de Saturne a justement lieu le 17 mai 2017, à peine un mois avant l'opposition de 2017. Les anneaux apparaitront donc déployés dans toute leur splendeur autour de Saturne, augmentant d'autant la luminosité apparente de l'ensemble.
À titre d'exemple, lors de l'opposition la plus proche du dernier équinoxe, de printemps Nord, en août 2009, la magnitude maximale de Saturne n'était que de 0,5, et ce malgré une distance à la Terre plus réduite (8,4 contre 9 UA en 2017), car les anneaux, vus par la tranche, étaient quasiment invisibles. Le point de l'orbite de Saturne le plus près du Soleil, qu'on appelle le périhélie, coïncide presque avec son solstice d'hiver Nord. Cette saison est donc la plus favorable pour observer la planète, car elle est alors à la fois plus proche et avec ses anneaux inclinés vers la Terre : elle apparait donc à la fois plus lumineuse et plus large dans un télescope. Par exemple, au dernier solstice d'hiver Nord, en 2002, Saturne était plus proche du Soleil, et donc de la Terre (8 UA), qu'en 2017 (9 UA), et avec les anneaux bien visibles sa magnitude a atteint -0,5. En terme de luminosité, l'opposition la plus défavorable de la dernière "année saturnienne" a eu lieu en 1995, lors de l'équinoxe précédent, d'automne Nord, avec une magnitude de 0,67.
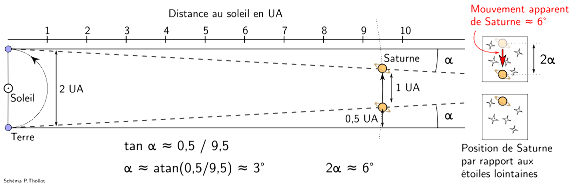
La prochaine opposition montrant Saturne aussi lumineuse que celle de 2017 n'aura pas lieu avant 2028, à l'approche du prochain solstice d'hiver Nord, en 2032. Entre temps, les 4 années encadrant le prochain équinoxe (le 5 mai 2025), offriront des spectacles rares : des transits des satellites de Saturne et de leurs ombres devant la planète, observables par les télescopes professionnels. Dans l'année autour de l'équinoxe, de rares transits de Titan et de son ombre seront même observables (une demi-douzaine au plus seront visibles de France métropolitaine de novembre 2024 à janvier 2025, mais hélas pas pendant l'opposition). Il faudra pour cela un bon instrument amateur, permettant un grossissement supérieur à 100x de qualité, car l'ombre de Titan fera moins d'une seconde d'arc (1") sur le disque de Saturne ! Ces transits sont rares car Titan orbite autour de Saturne à une distance d'environ 10 fois le diamètre de la planète, qui ne représente donc qu'environ arctan(1/10) ~ 5,7° d'angle vu depuis Titan. Cet angle étant petit devant l'obliquité du système de Saturne, ce n'est que proche de l'équinoxe que l'ombre de Titan se trouve projetée sur le disque de Saturne.
Opposition et mouvement rétrograde – La parallaxe
Les déplacements vrais que réalisent Jupiter et Saturne autour du Soleil se font vers l'Est (en regardant le système solaire par le Nord, dans le sens trigonométrique direct, inverse des aiguilles d'une montre). Depuis la Terre, d'une année à l'autre, c'est effectivement ce qu'on observe. Cependant, les quelques mois autour de l'opposition sont particuliers : Jupiter et Saturne semblent "reculer" dans le ciel (c'est-à-dire se déplacer vers l'Ouest) d'une nuit à l'autre. C'est aussi le cas pour la planète Mars. On parle alors de mouvement "rétrograde" (ou "rétrogradation"), par opposition au mouvement vrai "prograde" (vers l'Est), visible hors des périodes d'opposition.
À quoi est due cette rétrogradation apparente ? Au fait que la Terre tourne plus près et plus vite autour du Soleil que ces planètes (la Terre fait un tour en 1 an, contre environ 12 ans pour Jupiter et 30 ans pour Saturne), et, ce faisant, elle les "double par l'intérieur" régulièrement. Au cours de ce dépassement, le point de vue que porte un observateur terrestre sur Jupiter ou Saturne change par rapport aux étoiles en arrière-plan (des centaines de milliers de fois plus éloignées). L'effet est analogue à ce que l'on constate en tenant son pouce levé devant soi bras tendu, immobile, en le regardant alternativement avec chaque œil : si l'on ouvre d'abord l'œil droit, puis le gauche, le pouce semble s'être déplacé vers la droite par rapport à l'arrière-plan. Ce changement de position apparente d'un objet du fait du changement de position de l'observateur est nommé la parallaxe. Elle a eu, et a toujours, un rôle majeur en astronomie.
Examinons le détail du phénomène pour Saturne, pour laquelle il est encore assez tôt (au jour où sont écrites ces lignes) pour remarquer bientôt le changement de sens de son mouvement apparent. Sur l'échelle de temps d'une opposition (prenons 6 mois, pour simplifier) le mouvement propre de Saturne est relativement faible. Orbitant en moyenne à 9,5 UA, Saturne dessine une orbite d'environ 2.π x 9,5 = 60 UA de longueur, qu'elle parcourt en environ 30 ans. En 6 mois, Saturne parcourt donc "seulement" 1 UA (à une vitesse proche de 10 km/s tout de même). Dans le même temps de six mois, la Terre se déplace (à 30 km/s) d'un "côté" à l'autre d'un diamètre de son orbite, soit, par définition, de 2 UA. Le schéma, Figure 6 ci-dessous, permet alors de comprendre ce qu'il se passe pour un observateur terrestre.
Dans l'intervalle de 6 mois, Saturne se déplace d'environ 1 UA, la Terre de 2 UA. Trois mois avant l'opposition la Terre (rond bleu) et Saturne (avec anneaux) sont situées à leur position inférieure sur le schéma et Saturne est visible depuis la Terre, faisant un angle α avec la direction symbolisée par l'horizontale. Trois mois après l'opposition les planètes sont à leurs positions supérieures et Saturne est vue depuis la Terre sous un angle α dans l'autre sens. Au total le mouvement apparent de Saturne depuis la Terre correspond à un mouvement "rétrograde" (par rapport à son mouvement vrai) de 2α.
En un temps donné, le déplacement de la Terre autour du Soleil est plus grand que celui de Saturne. En conséquence, par rapport à une direction donnée vers les étoiles (l'horizontale sur le schéma), étoiles des centaines de milliers de fois plus éloignées que Saturne et que l'on peut donc considérer à l'infini, le sens du mouvement apparent de Saturne est dominé par le mouvement de la Terre autour du Soleil, et non par le mouvement vrai de Saturne. Ainsi, pour un observateur terrestre qui passe d'un côté à l'autre du Soleil, Saturne semble "reculer" vers l'Ouest sur le fond des étoiles, mais c'est un effet de changement de point de vue : son mouvement vrai la fait bien "avancer" dans le même temps vers l'Est autour du Soleil.
Les deux vidéos ci-dessous (Figure 7 et Figure 8), générées avec le logiciel open sourceCelestia, permettent de visualiser l'opposition de Saturne soit depuis le Soleil (on ne voit alors que le mouvement vrai, prograde), soit en suivant la Terre dans sa révolution autour du Soleil (on voit alors le mouvement apparent depuis la Terre, rétrograde).
Source - © 2017 Simulation Celestia Figure 7. Animation du système solaire centrée sur Saturne, où la prise de vue suit le Soleil, de mars à octobre 2017, au cours de l'opposition de Saturne Observer le mouvement prograde vers l'Est (ici vers la gauche) de Saturne par rapport aux étoiles d'arrière-plan des constellations du Serpentaire et du Sagittaire. | Source - © 2017 Simulation Celestia Figure 8. Animation du système solaire centrée sur Saturne, où la prise de vue suit la Terre dans sa révolution autour du Soleil, de mars à octobre 2017, au cours de l'opposition de Saturne Observer l'établissement, rapide en début d'animation, d'un mouvement rétrograde vers l'Ouest (ici vers la droite) de Saturne par rapport aux étoiles d'arrière-plan des constellations du Serpentaire et du Sagittaire. Vers la fin de l'animation le mouvement se ré-inverse et redevient prograde. La grille des coordonnées écliptiques, projetée sur l'arrière-plan, permet de mesurer l'amplitude de la rétrogradation apparente de Saturne, d'environ 6° (un peu plus d'un "carreau" de 5° de la grille). |
Ce mouvement rétrograde des planètes extérieures à la Terre, à l'explication simple, pose beaucoup plus de problèmes si l'on postule de manière erronée que les planètes tournent autour de la Terre… Afin d'expliquer les rétrogradations, le modèle géocentrique de Ptolémée (lui-même basé sur les travaux de ces prédécesseurs, Hipparque notamment), ne fait pas vraiment tourner les planètes autour de la Terre : elles tournent sur un petit cercle, nommé épicycle, dont le centre, immatériel, tourne sur un grand cercle autour de la Terre. Il faut donc la combinaison de ces deux mouvements circulaires pour expliquer le mouvement rétrograde des périodes d'opposition. Un modèle héliocentrique ne fait au contraire appel qu'à un seul mouvement de révolution, autour du Soleil, et sans épicycle centré sur un point immatériel.
Au premier ordre, un modèle héliocentrique est donc à la fois plus simple et plus parcimonieux. On peut dès lors, pour simplifier, présenter cet argument comme décisif en faveur de l'héliocentrisme… Malheureusement, dans le détail, le changement de point central ne suffit pas à décrire les mouvements précis des planètes plus simplement. Pour approcher finement les mouvements planétaires, Copernic, dont le système héliocentrique a été publié en 1543, avait dû introduire aussi des cercles supplémentaires à ceux des orbites planétaires, car Copernic utilisaient des orbites circulaires. Comme Kepler l'a découvert vers 1605 et publié en 1609, les orbites des planètes autour du Soleil sont elliptiques, et non circulaires et c'est seulement cette modification qui permet de rendre compte élégamment des déplacements apparents de chaque planète par une trajectoire « mathématiquement simple ».
De la parallaxe planétaire à la parallaxe stellaire
Le mouvement rétrograde apparent des planètes extérieures est dû à la parallaxe entre les planètes du système solaire : on peut éventuellement parler de parallaxe planétaire. Seule la parallaxe planétaire est visible à l'œil nu (de quelques degrés pour Jupiter et Saturne à une bonne quinzaine de degrés pour Mars), mais le phénomène de parallaxe est généralisable à d'autres objets... On définit ainsi la parallaxe d'un objet céleste comme la moitié de celle qu'il montre du fait du mouvement de la Terre autour du Soleil en 6 mois (un diamètre de son orbite, soit 2 UA). Dit autrement, c'est, pour un observateur se décalant de 1 UA dans le système solaire, l'amplitude du mouvement apparent d'un objet céleste sur le fond du ciel. Dans l'analogie du pouce tendu devant soi, les deux yeux seraient écartés de 1 UA !
L'amplitude de la parallaxe pour les objets hors du système solaire est cependant extrêmement faible. Même pour l'étoile la plus proche, Proxima Centauri, elle approche à peine une seconde d'arc (1"), c'est à dire 1/3600e de degré ! Cela correspond à la taille apparente d'une pièce de 1 euro qui serait tenue par quelqu'un au sommet de la Tour Eiffel, mais vue depuis… la butte Montmartre, à près de 5 km de là ! À titre de comparaison, la taille apparente de Jupiter à l'opposition est de l'ordre de 45 fois supérieure, et il faut déjà un bon télescope pour en trouver l'image confortable...
La parallaxe stellaire étant minuscule, il a fallu attendre le milieu du XIXème siècle pour que les progrès instrumentaux permettent aux astronomes de la détecter (la première fois par Bessel, en 1838, pour une étoile dont on avait remarqué un mouvement propre continu de plusieurs secondes d'arc par an, laissant supposer une relative proximité, 61 Cygni). Avant cette première mesure, on avait déjà pu conclure, puisqu'on ne voyait pas de parallaxe de quelques secondes d'arc, que les étoiles étaient extrêmement éloignées !
Depuis qu'on arrive à la mesurer, la parallaxe stellaire est toujours la méthode utilisée pour mesurer les distances des étoiles "relativement" proches de nous. Cette méthode est associée à une unité de distance géométriquement liée à la parallaxe. Par définition, une parallaxe de 1 seconde d'arc correspond à une distance de 1 parsec : la parallaxe de l'étoile "tient" 1 fois par seconde d'arc (voir Figure 9, en haut). Une parallaxe plus petite correspond à une distance d'autant plus importante : par exemple, une étoile de 0,1 seconde d'arc de parallaxe (parallaxe 10 fois plus petite – il en "tient" 10 par seconde d'arc) se trouve à 10 parsecs de la Terre (10 fois plus loin).
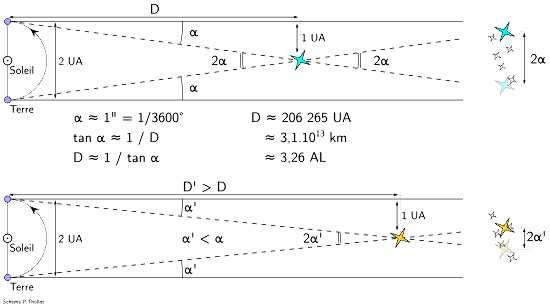
Figure 9. Représentation schématique de la parallaxe stellaire
À gauche, on a schématisé le Soleil et la Terre, avec sa révolution autour du Soleil au cours de 6 mois, pendant laquelle elle parcourt 2 UA.
Au centre, on a représenté deux étoiles lointaines (en bleu et jaune) sans conserver l'échelle utilisée pour l'orbite de la Terre : elles sont en réalité beaucoup plus loin.
À droite, on a figuré le mouvement apparent de ces deux étoiles par rapport à d'autres, situées beaucoup plus loin, et donc apparemment immobiles.
En haut, une étoile bleue, située à une distance D de la Terre, montre en 6 mois un mouvement apparent d'un angle de 2α. Pour α = 1", par définition, D = 1 parsec. Comme α est très petit (α ≈ π/180/3600 ≈ 5.10-6 radian) on peut faire l'approximation trigonométrique α ≈ sinα ≈ tgα ≈ 1/D, d'où on tire que la distance D ≈ 1/α ≈ 206265 UA, soit 3,26 AL (année-lumière).
En bas, une étoile jaune située à une distance de la Terre D', supérieure à D, montre un mouvement apparent α', inférieur à α.
Une simple relation trigonométrique (voir Figure 9, ci-dessus) implique que le parsec vaut environ 200 000 UA ! L'UA (≈ 150 millions de km) donne l'ordre de grandeur des distances dans le système solaire ; les étoiles les plus proches sont à quelques parsecs ; donc les distances interstellaires sont de l'ordre du million de fois plus grandes que les distances interplanétaires, pourtant déjà difficiles à appréhender. Le parsec vaut environ 3,1.1013 km, ce qui est du même ordre de grandeur que l'année-lumière (AL, avec 1 AL ≈ 0,95.1012 km ; 1 parsec ≈ 3,26 AL). Comme l'année-lumière, le parsec est bien une unité « astronomique » !
Depuis 1997, le catalogue le plus précis des parallaxes stellaires dans notre galaxie est celui construit à partir des mesures du télescope spatial Hipparcos de l'ESA, lancé en 1989. La parallaxe des étoiles du catalogue Hipparcos atteint une précision de l'ordre du millième de seconde d'arc (ou milli-arc-seconde – mas). Cette précision permet d'estimer des distances correctes jusqu'à l'ordre de l'ordre du millier de parsecs, ou quelques milliers d'AL. C'est peu en comparaison avec la taille de notre galaxie (100 000 AL de diamètre).
À l'échelle de la Galaxie ("notre" galaxie, la Voie Lactée), d'autres méthodes ont historiquement pris le relais de la parallaxe. L'une d'elles est basée sur le rapport entre la luminosité intrinsèque de certaines étoiles variables (les "céphéides"), qui dépend de leur période, et celle effectivement observable, qui donne donc leur distance. Courantes, certaines céphéides sont assez proches pour que la mesure de leur parallaxe ait permis de connaître leur luminosité intrinsèque. Celles plus éloignées servent alors de "bornes de mesure" dans la Galaxie.
Mais la parallaxe n'a pas dit son dernier mot et l'Europe, il est parfois bon de le rappeler, est à la pointe en ce domaine. Le télescope spatial Gaia de l'ESA (voir la page de la mission Gaia sur le site du CNES, l'agence spatiale française), lancé fin 2013, a ainsi été conçu pour cataloguer 1 milliard d'étoiles (la Galaxie en compte encore 100 fois plus) en portant la précision sur la parallaxe des dizaines de millions d'étoiles les plus brillantes à une dizaine de micro-arc-secondes. Il devrait donc permettre de mesurer des distances d'étoiles brillantes à l'échelle de toute la Galaxie, et même dans les nuages de Magellan, petites galaxies satellites de la Voie Lactée. Jusqu'à environ 50 parsecs du système solaire, Gaia devrait même permettre de caractériser les distances et propriétés de toutes les étoiles présentes (des géantes rouges aux naines blanches ; plusieurs dizaines de milliers). Au-delà le catalogue ne sera pas exhaustif car les étoiles faibles seront invisibles au télescope. Le catalogue Gaia définitif ne devrait être terminé qu'en 2020, mais une première version, sans données de parallaxes, a déjà été publiée fin 2016 : elle contient les positions de 1 milliard d'étoiles, dont 99% n'étaient auparavant pas référencées !
Malgré la précision de Gaia, les parallaxes des galaxies (autres que les galaxies satellites de la Voie Lactée) sont bien trop faibles pour être mesurables, et les distances intergalactiques sont mesurées par d'autres critères que la simple géométrie.