Article | 06/10/2005
Fonte de la banquise (glace de mer) et élévation du niveau marin
06/10/2005
Résumé
Pourquoi la fonte de la banquise n'influence pas le niveau de la mer de manière significative. Processus à facteurs multiples et ordres de grandeur relatifs.
Table des matières
La question
Voici, ci-dessous, la question telle qu'elle nous a été posée.
Suite à l'article concernant "l'élévation du niveau marin par fonte des glaces", je suis assez étonné d'y relever l'affirmation suivante : « la fonte des glaces de mer (banquises) n'influence pas le niveau marin », suivie de l'explication : « en effet, comme les glaces de mer flottent, elles déplacent un volume d'eau de mer dont le poids est égal au poids de la glace (principe d'Archimède) ». « Si cette glace océanique fond, l'eau de fonte occupe exactement le volume d'eau de mer que la glace occupait, sans modifier le niveau marin », cette affirmation suivie de deux expérimentations :
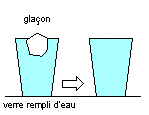
- un verre d'eau douce dans lequel un glaçon en fondant ne modifie pas le niveau de l'eau (sensé représenter les glaces de mer) ;
- un verre d'eau dans lequel un glaçon est ajouté et modifie effectivement ce niveau (sensé représenter les glaces continentales).
Si cette seconde expérimentation tombe sous le sens, l'ajout de matière ne pouvant qu'entraîner une hausse de niveau de l'eau, il n'en va pas de même pour la première qui, bien qu'obéissant au principe d'Archimède, ne correspond en rien à la situation des "glaces de mer" qui flottent, elles, sur de l'eau salée dont le poids volumique est supérieur à celui de l'eau douce. Ce fait implique que la glace émergera davantage en eau saline qu'en eau douce et qu'elle creusera un déplacement moindre. Or, comparé au cas de l'eau douce, le volume de déplacement étant réduit et le volume d'eau de fonte restant inchangé, il semble évident que si le niveau du liquide reste inchangé en eau douce, il monte en eau salée. Cette conclusion peut être facilement démontrée par la fonte de glaçons dans 2 verres d'eau, l'un rempli d'eau douce et l'autre d'eau salée. La différence de niveau après la fonte des glaçons sera d'autant plus évidente que le diamètre des verres sera réduit (long-drink) et que la quantité de sel et de glaçons ne soit pas comptée, ces glaçons ne devant évidemment pas reposer sur le fond du verre.
La réponse
Avant de répondre précisément à votre question, nous pouvons dire en préambule que votre question pose le problème de la notion d'ordre de grandeur, de valeur ou de phénomène du 1er et 2ème ou 3ème ordre. Très souvent, en sciences expérimentales ou naturelles, on simplifie en négligeant les effets de 2ème ou 3ème ordre, surtout si ces effets, réels, sont perdus dans d'autres aussi important mais de tout autres causes. La fonte des glaces continentales fait varier le niveau de la mer d'environ 100 m (-120 m lors du dernier maximum glaciaire, +80 m si Groenland et Antarctique fondaient). L'élévation, réelle, que vous proposez, que nous avons négligée dans l'article "l'élévation du niveau marin par fonte des glaces", et que nous détaillerons ci-dessous se chiffre en millimètres, c'est-à-dire 105 fois moins. Il est donc tout à fait légitime de la négliger, d'autant plus qu'à la fonte des glaces (continentale ou marine) se superpose d'autres variations du niveau des mers qui peuvent être d'ordre de grandeur voisin que ces quelques millimètres (augmentation du stockage d'eau et de sédiments dans les lacs de barrage, élévations de la Scandinavie et du Canada qui "prennent de la place" dans la mer et la font donc monter, invasion de plaine basse par la mer qui fait baisser l'océan…).
Sur ce, vous aviez raison, car en toute rigueur le schéma (figure 1) de l'article "l'élévation du niveau marin par fonte des glaces", n'est valable que si l'eau qui constitue la glace et l'eau dans lequel flotte le glaçon ont la même salinité (et donc la même masse volumique lorsqu'elles se retrouvent à la même température).
Or il est vrai que les valeurs de salinité de la banquise (glace formée à partir de l'eau de mer) peuvent se discuter. Lorsque vers -1,9°C, la mer commence à geler, des cristaux d'eau douce se forment mêlés à une saumure (sursalée par rapport à l'eau de mer initiale).
- si la banquise est constituée de cette saumure et/ou de cristaux de sel ou de sulfates piégée entre les cristaux d'eau douce, sa masse volumique moyenne peut se rapprocher de celle de l'eau de mer initiale ;
- si la banquise n'est constituée que de cristaux d'eau douce, alors on se rapproche du cas de votre expérience avec un glaçon d'eau douce dans de l'eau salée et on peut en effet s'attendre à une variation du niveau de l'eau après fonte du glaçon.
Mais, il faut se rendre compte que votre expérience dans un verre d'eau (long-drink) est un peu loin de ce qui se passe en réalité en raison :
- des problèmes d'échelle : le rapport des surfaces banquise/océan total ne correspond pas au rapport surface du glaçon/section du verre (surtout si c'est un long-drink), le rapport des volumes pose le même problème. Le modèle du verre de long-drink n'est pas correctement dimensionné. Il faudrait une bassine ou un cristallisoir avec un glaçon car le rapport surface du glaçon/surface totale de la bassine doit être voisin de 1/10 compte tenu des valeurs réelles des surfaces de l'océan et des banquises.
- des problèmes de salinité : la glace de mer s'est formée à partir de l'eau de mer. La situation réelle est vraisemblablement intermédiaire entre les deux cas extrêmes cités précédemment (glace d'eau douce et glace de même salinité que l'eau de mer). D'ailleurs, dans la littérature, la salinité de la glace de banquise est variable de 0 à 10 g/L et sa masse volumique varie entre 1000,86 et 1000,92 kg/m3 ;
- de l'existence de courants (par exemple la saumure salée et froide plonge en profondeur).
Plaçons-nous dans le cas "doublement extrême" d'une glace de mer constituée uniquement d'eau douce et d'une fonte totale de cette banquise.
Expliquons qualitativement les conséquences de cette fonte.
Le volume total de la banquise a, d'après le principe d'Archimède, la même masse que le volume d'eau de mer déplacé par la partie immergée de la banquise. Comme la glace de la banquise a une masse volumique inférieure à celle de l'eau de mer, il est donc normal que la banquise flotte et dépasse donc du niveau marin. Le rapport entre l'épaisseur la racine et l'épaisseur de la banquise est égal au rapport entre la masse volumique de la glace et celle de l'eau océanique.
Lorsque la banquise fond, l'eau de fonte qui en résulte a une masse volumique plus élevée que la glace et occupe donc un volume moindre que celui de la banquise. Reste à comparer le volume occupé par cette eau de fonte (Vf) à celui qu'occupait la partie immergée de la banquise (Vi).
- Si Vf>Vi, alors le niveau de la mer s'élève.
- Si Vf=Vi, le niveau de la mer reste constant.
- Si Vf<Vi, le niveau de la mer s'abaisse.
Ces volumes dépendent uniquement des masses volumiques des différents types d'eau (glace, eau de fonte et eau océanique).
Estimons quantitativement la variation du niveau marin engendrée par cette fonte de la totalité des glaces de mer.
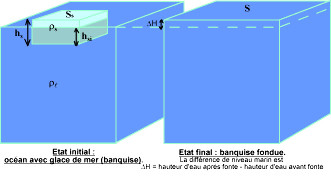
Les notations utilisées sont indiquées dans la légende de la figure 2.
Figure 2. Représentation schématique de la fonte d'une banquise
- ms : masse de l'eau solide (banquise), comme il y a conservation de la masse de l'eau après changement d'état ms = mf où mf= masse de l'eau résultant de la fonte de la banquise.
- ρs : masse volumique de l'eau solide (banquise)
- Ss : surface de la banquise
- hs : épaisseur totale de la banquise
- hsi : épaisseur immergée de la banquise
- ρℓ : masse volumique de l'eau liquide (océan)
- ρf : masse volumique de l'eau résultant de la fonte de la glace
- hf : hauteur d'eau liquide (océan) dans l'état final : niveau de la mer après fonte de la banquise
- S : surface totale de l'océan (surface de la banquise comprise)
Calculons la différence de volume (ΔV) entre le volume d'eau libéré par la fonte de la banquise et le volume d'océan occupé par la banquise :
ΔV = (ms/ρf ) - Ss. hsi = Ss. hs.ρs /ρf - Ss. hsi
Or la banquise est en équilibre donc d'après le principe d'Archimède :
- poids de la banquise = poussée d'Archimède de l'océan sur la banquise
- poids de la banquise = poids du volume d'océan déplacé par la banquise
Avec les notations précédentes et g, constante de gravité :
- ρs. g . hs. Ss = ρℓ . g . hsi . Ss
- soit, ρs. hs= ρℓ . hsi, après simplification.
- d'où, hsi = ρs. hs/ ρℓ.
ΔV devient donc ΔV = Ss. hs.ρs /ρf - Ss. hs. ρs /ρℓ = Ss. hs.ρs (1 /ρf - 1 /ρℓ)
La variation de hauteur de l'océan notée ΔH, s'écrit alors :
- ΔH = ΔV/S = (Ss. hs.ρs /S)(1 /ρf - 1 /ρℓ)
On vérifie bien que si l'eau de fonte et l'océan ont la même masse volumique c'est-à-dire si ρf = ρℓ alors ΔH=0.
Mais avec les valeurs numériques (en gras : sont celles directement utilisées dans la formule) ci-dessous, on trouve une variation de hauteur de 4,4 mm, ce qui est vraiment négligeable et ce d'autant plus que cette valeur correspond au cas où la banquise supposée composée uniquement d'eau douce fondrait dans sa totalité.
Océan | Banquise totale (arctique + antarctique) cf. Note | Eau de fonte de la banquise | |
Volume total (km3) | 64.000 | ||
Épaisseur (m) | 3.790 | 1,89 | |
Surface (km2) | 34.000.000 | ||
Masse volumique (kg/m3) | 917 (920 à -45°C) | ||
Salinité (g/L) | 35 | 0 | 0 |
Température (°C) | 5 | 0 | 0 |
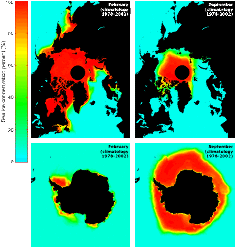
Le volume total et l'épaisseur moyenne de la banquise ont été calculés en prenant les valeurs maximales (figure 3) données pour la banquise arctique (15 millions de km2 et 3 m d'épaisseur) et pour la banquise antarctique (19 millions de km2 et 1 m d'épaisseur). Ces valeurs ont tendance à décroître depuis 25 ans. L'épaisseur moyenne a été obtenue avec la formule suivante (15x3 +19x1)/(15+19) ≈ 1,89 m.
Source - © 2002 National Snow and Ice Data Center, Univ. of Colorado, Boulder
Figure 3. Extensions minimales et maximales des banquises arctique (en haut) et antarctique (en bas)
La couleur représente la concentration en glace de l'eau de mer : bleu pour la mer sans glace, rouge pour la glace.
Enfin n'oublions pas que pour l'instant la dilatation thermique de l'océan est le facteur principal de variation du niveau marin en cas de réchauffement du climat. La fonte de la banquise quant à elle, n'influence pas les variations du niveau de la mer, mais ce n'est pas pour autant qu'elle est sans conséquence sur l'évolution du climat. En effet, la banquise, par sa couleur claire, a un fort pouvoir de réflexion des rayons solaires, et donc un rôle dans les variations de l'albédo de la surface de la Terre. Une augmentation de sa taille favorise le refroidissement naturel de la Terre alors que sa fonte amplifie le réchauffement climatique en diminuant l'albédo moyen de la surface terrestre.