Article | 31/03/2000
Modélisation de l'effet Coriolis
31/03/2000
Résumé
Expérience avec un saladier permettant de comprendre l'enroulement des nuages par effet Coriolis.
Table des matières
Idée originale : Gérard Vidal, ENS-Lyon. Validation scientifique de ce dossier : François Chamaraux et Maxime Clusel, élèves de deuxième année au Magistère des Sciences de la Matière de l'ENS-Lyon. Expérimentation pédagogique : Benoît Urgelli avec Gary Benattar, élève en classe de troisième à Lyon.
Ce travail a été réalisé en décembre 1999 au Laboratoire des Sciences de la Terre de l'ENS de Lyon, en collaboration avec le Laboratoire de Sciences Physiques.
Problématique
Les questions
Observation des figures d'enroulement des nuages autour de dépressions atmosphériques. Ces figures sont des cyclones.
Hémisphère Nord : on constate que l'enroulement est dans le sens anti-horaire. Hémisphère Sud : on constate que l'enroulement et dans le sens horaire. Sur les deux images, on constate qu'il n'y a pas d'enroulement à l'équateur.
Comment apparaissent ces figures, où apparaissent-elles ? Comment expliquer les différents sens d'enroulement entre l'hémisphère Nord et Sud ? Pourquoi n'y a-t-il pas de figures d'enroulement à l'équateur ?
hypothèses formulées
Première hypothèse
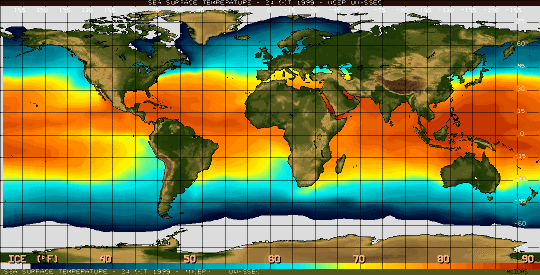
La différence de température entre les hémisphères Nord et Sud changerait l'enroulement des nuages. Or, sur une carte des températures à la surface du globe, on constate qu'il y a le même écart de température dans les deux hémisphères.
Figure 3. Températures océaniques de surface
Conclusion : ce n'est pas la différence de température qui permet de comprendre l'enroulement des nuages.
Seconde hypothèse
Il y a plus de masse continentale dans l'hémisphère Nord que dans l'hémisphère Sud. Avec cette hypothèse, difficile d'expliquer l'enroulement inverse.
Troisième hypothèse
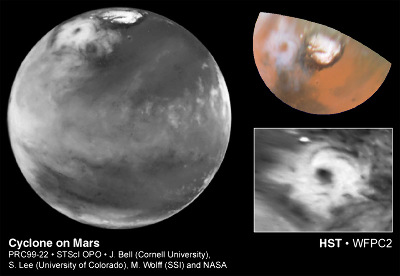
L 'éloignement de la planète par rapport au Soleil. On observe alors d'autres planètes du système solaire ayant une atmosphère.
Sur Vénus, planète dont le sens de rotation est rétrograde : pas de figures d'enroulement. Par contre, comme sur la Terre, il y a des mouvements d'enroulements des masses atmosphériques sur Mars et sur les planètes gazeuses (Jupiter),.
Conclusion : ce n'est pas l'éloignement par rapport au Soleil qui explique l'existence de figures d'enroulement cyclonique.
Observations complémentaires : vitesse de rotation des planètes
Si on compare les mouvements sur Vénus et sur la Terre : la Terre tourne sur elle-même en 23,934 heures alors que Vénus tourne sur elle-même en 243 jours (avec le sens de rotation inverse de celui de la Terre). Vénus tourne donc beaucoup plus lentement que les autres planètes ayant une atmosphère. On peut donc penser que la présence de figures d'enroulement est liée à la vitesse de rotation des planètes à atmosphère.
On va donc essayer de montrer que l'existence de figures d'enroulement cyclonique est liée à la rotation de la planète. Pour cela, on désire construire un modèle tournant à des vitesses de rotation différentes.
Dispositif
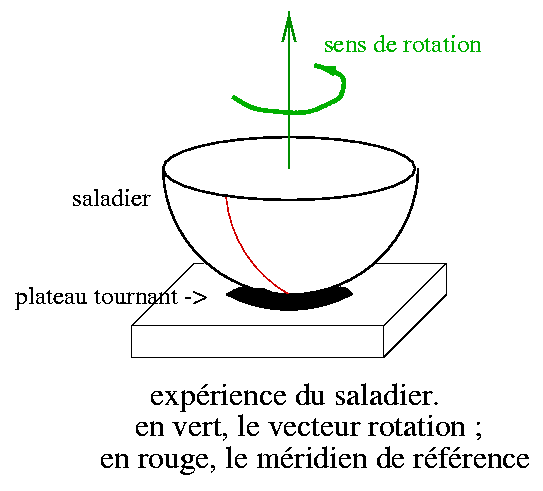
Montage
La maquette comprend :
- 1 saladier transparent de 30 cm de diamètre, sur lequel on trace une ligne verticale correspondant à un méridien ;
- 1 tour de potier ;
- un rhéostat ;
- un tachymètre digital ;
- de la pâte à fixer (type "Patafix)" ;
- du miel coloré avec de l'encre bleu ;
- 5 billes d'écolier de masses différentes.
Figure 7. Le montage
Préparation technique
Fixer la base du saladier au tour de potier à l'aide de la pâte à fixe.
À l'aide d'un rhéostat (alimentation à tension variable de 0 à 10V) que l'on branche sur l'alimentation du tour de potier, on peut régler électriquement la vitesse de rotation du dispositif.
La mesure de la vitesse de rotation se fera avec un tachymètre digital (données en tours par minute). Les billes sont trempées dans le miel coloré (si le miel est trop visqueux, on peut le chauffer quelques secondes au four à micro-ondes)
Déposer à l'aide d'un spatule la bille enduite de miel au fond du saladier (pôle Nord ou pôle Sud suivant le sens de rotation du tour). Réglage de la vitesse à 5V sur le rhéostat, ce qui correspond à 180 t/min environ. Ne pas dépasser 1 A lors de l'alimentation du tour de potier.
Ce dispositif ne nous a pas permis, malheureusement, de faire varier la vitesse de rotation.
Par contre on peut facilement faire tourner dans un sens, puis dans l'autre. Faire varier également la masse de la bille.
Résultats
Résultats en faisant varier le sens de rotation du dispositif
Sous l'effet de la force centrifuge, la bille monte le long de la paroi du saladier. Mais sa trajectoire n'est pas méridienne. Elle est déviée à droite ou à gauche par rapport au méridien suivant le sens de rotation horaire ou anti-horaire du tour de potier. Cette nette déviation de la bille est liée à l'existence de la "force" de Coriolis.
Deuxième série d'expériences, en faisant varier la masse de la bille
Pour chaque bille, on mesure l'angle de déviation de la trajectoire par rapport au méridien pour un sens et une vitesse de rotation fixés.
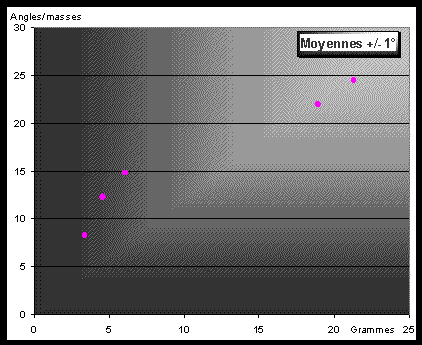
Masses des billes | Angle de déviation 1ère série de mesures (+/-1°) | Angle de déviation 2e série de mesures (+/-1°) | Moyenne des angles de déviation |
M1 = 3,4 g | 7,5° | 9° | 8,25° |
M2 = 4,6 g | 16,5° | 8° | 12,25° |
M3 = 6,1 g | 15° | 14,5° | 14,75° |
M4 = 18,9 g | 21° | 23° | 22° |
M5 = 21,3 g | 26° | 23° | 24,5° |
Il est souhaitable de réaliser une troisième série d'expérience pour diminuer les incertitudes. À partir de ce tableau de résultat on peut tracer la courbe ci-dessous.
Figure 8. Courbe expérimentale
On constate que plus la bille est lourde, plus elle est déviée par rapport à la trajectoire méridienne.
L'effet Coriolis dépend donc du sens de rotation du dispositif et de la masse de l'objet qui se déplace dans le repère tournant. Avec un dispositif plus performant, on aurait pu montrer le rôle de la vitesse de rotation sur l'effet Coriolis.
Source - © 2000 Planet-Terre - ENS de Lyon
Modélisation de l'effet Coriolis
Durée ~ 5min20s.
Retrouvez l'explication du montage dans Expérience sur les forces d'inertie.
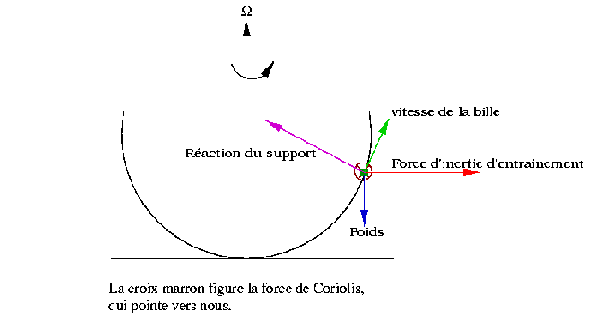
Bilan des forces
Figure 9. Le bilan des forces
Dans le référentiel tournant, la bille est soumise à son poids, à la force d'inertie d'entraînement, à la force de Coriolis, et à la réaction du support. C'est la force d'inertie d'entraînement qui impose à la bille de monter le long des parois, et la force de Coriolis dévie la bille, donnant ainsi une trajectoire en forme de spirale.