Article | 23/10/2000
Évolution saisonnière de l'insolation et de la température en un lieu donné
23/10/2000
Résumé
Les variations saisonnières de température en relation avec la variation de l'angle d'incidence des rayons solaires.
Table des matières
La question
Données récoltées à Paris | Janv | Fév | Mars | Avr | Mai | Juin | Juil | Aout | Sept | Oct | Nov | Déc |
Irradiation globale (en kJ/m2/j) | 3000 | 5200 | 9400 | 14400 | 17100 | 18900 | 19000 | 16800 | 12900 | 7500 | 4000 | 2500 |
Température moyenne (en °C) | 1 | 2.5 | 6.5 | 11 | 15 | 18 | 20 | 19.5 | 16 | 11 | 5.5 | 1.5 |
« À partir du tableau ci-dessus, j'ai obtenu une courbe mettant en relation température moyenne en fonction de l'irradiation (dans le but de faire un sujet de devoir). »
« Un lissage (important) permet-il d'affirmer qu'il y a proportionnalité ? Peut-on utiliser ce graphe pour introduire la notion d'effet de serre... En effet, il semble y avoir une différence nette entre les mois d'automne et de printemps : pour une même énergie reçue, la température est plus élevée en automne qu'au printemps. Est-ce dû au taux de CO2 ? »
La réponse
Un point donné choisi n'importe où à la surface de la Terre (ici Paris) voit l'angle d'incidence des rayons solaires osciller au cours de l'année d'un maximum à un minimum et vice versa.
Cette oscillation est liée au fait que l'axe de rotation de la Terre sur le plan de l'écliptique est inclinée et orientée toujours dans la même direction (celle de l'étoile polaire). L'orientation de l'axe de rotation par rapport aux rayons solaires soleil varie donc...
On peut modéliser simplement cette oscillation à l'aide de la maquette de l'Observatoire de Lyon.
Source - © 2001 Claude Piguet, Obs. Saint Genis Laval, Lyon
Figure 1. Maquette Terre - Soleil
La Terre réagit comme tout autre corps susceptible de s'échauffer ou de se refroidir. La plupart de l'énergie responsable de l'échauffement de la surface de la Terre vient du soleil (relayé pour une part par l'atmosphère). Au premier ordre, la quantité d'énergie reçue dépend de l'angle d'incidence des rayons solaires.
Ainsi, pour un point géographique donné, l'évolution de l'énergie reçue au cours du temps est matérialisée par une courbe périodique (et si l'énergie solaire émis est supposée constante, c'est une courbe sinusoïdale!).
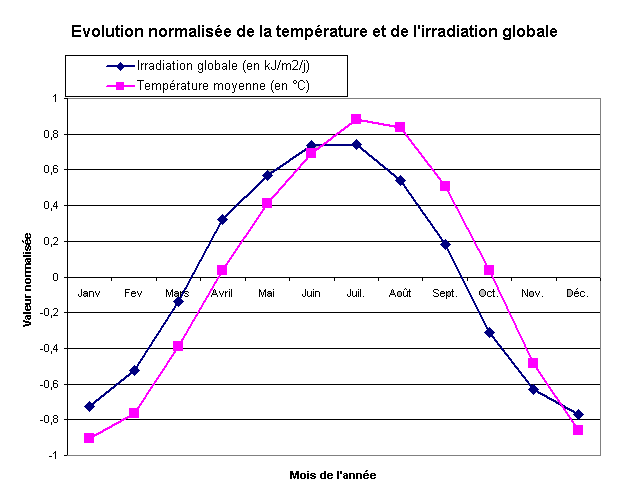
Pour pouvoir comparer la variation en fonction de temps de l'énergie reçue (signal d'entrée) et de la température (signal réponse), on normalise la valeur de l'énergie en pointant (E-Emoy) / Emoy en fonction du temps. (Emoy est l'énergie moyenne reçue au point géographique considéré).
On réalise le même traitement mathématique pour pointer la température normalisée (T-Tmoy) / Tmoy en fonction du temps.
Source - © 2000 Pierre Thomas, ENS de Lyon | Source - © 2000 Pierre Thomas, ENS de Lyon |
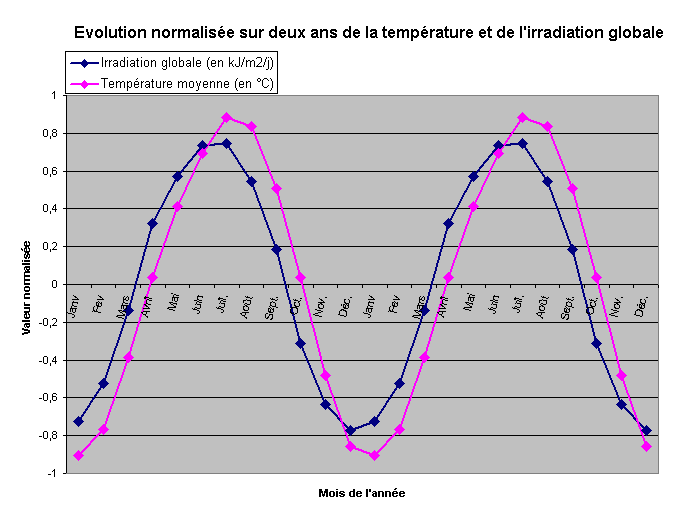
Évolution normalisée de la température et de l'irradiation totale sur un et deux ans.
On observe alors que l'allure de la courbe des températures est identique à celle de l'énergie reçue MAIS "décalée" dans le temps, avec un retard.
Ce décalage temporel correspond à l'inertie thermique de la planète.
Pour vous en convaincre, vous pouvez observer les animations de la réponse de Pierre THOMAS qui montrent très clairement ce "décalage".
Une observation plus fine de ces animations met en évidence le décalage différentiel entre continents et océans qui n'ont pas les mêmes propriétés thermiques.
Voir aussi
La réponse de Pierre THOMAS, Professeur à l'ENS de Lyon.