Advection et convection

La question suivante fait suite à la conférence de Francis Albarède sur "La géochimie et la géodynamique du manteau" donnée dans le cadre du Plan Académique de Formation (académie de Lyon) sur le manteau terrestre :

« Le dictionnaire de géologie et le site de Météo-France donne la définition suivante de la convection et de l'advection : “...au sens météorologique, l'emploi du terme "convection" se limite au transport horizontal des propriétés de l'air, le transport vertical desdites propriétés étant désigné par un autre terme l'advection (il s'agit en fait de l'advection horizontale)...”. »

« Serait-il possible de définir clairement ces termes ? »

Vous m'avez fait toucher du doigt qu'une définition précise de la convection est très rarement donnée dans les livres, même lorsqu'ils y sont consacrés.

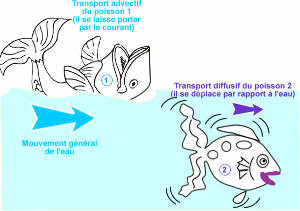
Tout d'abord, reprenons les définitions simples. Les transports d'un point à un autre se font soit par advection soit par diffusion. Imaginons des poissons dans une rivière. Le mouvement général de l'eau assure le transport advectif des poissons. Le mouvement des poissons par rapport à l'eau (par exemple en se repérant sur une feuille morte dérivant dans le courant) est le transport diffusif (figure 1).

Source - © 2005 Florence Kalfoun

Figure 1. Exemple de transport advectif et de transport diffusif

De façon générale, l'advection est le transport de chaleur, de matière, etc à la vitesse du milieu environnant et la conduction (ou diffusion) est le transport relatif par rapport au milieu environnant en mouvement.

Où se trouve la convection là-dedans? Je prends la définition du Landau et Lifschitz de Mécanique des fluides : "Les écoulements qui s'établissent dans un fluide soumis à l'action de la force de la pesanteur constituent ce que l'on appelle la convection naturelle". Ozisik (Transfert de chaleur, ma traduction) est encore plus précis: "Les variations de température dans un fluide créent un gradient de densité qui, dans un champ de pesanteur et sous l'effet de la poussée d'Archimède, donnera à son tour naissance à un mouvement convectif. Le mouvement du fluide déclenché par la poussée d'Archimède est appelé convection naturelle".

La convection est donc un mouvement qui résulte d'une instabilité gravitaire à l'intérieur d'un système déformable: on ne peut limiter cette instabilité aux effets thermiques sur la densité puisque dans l'océan, il est connu que le sel a un effet (la circulation océanique est dite convection thermo-haline), dans l'atmosphère l'humidité et le brouillard peuvent avoir un effet, et dans le manteau il est maintenant admis que la teneur en fer ne peut être ignorée et l'on parle de "panache compositionnel" pour le manteau sous l'Afrique du Sud. Les courants de turbidité sont aussi une forme de convection. Mais pour la simplicité de l'exposé, on peut se limiter à l'effet thermique: une zone chaude située en dessous d'un zone froide résulte en une inversion de densité et donc en une instabilité: toute fluctuation de position à la limite des deux zones déclenchera la convection si le remplacement de matériel lourd par du matériel léger libère de l'énergie, c'est-à-dire si la poussée d'Archimède peut produire du travail. La conversion de cette énergie en chaleur (dissipation) confère un caractère irréversible à la convection.

Dans le manteau, très visqueux, quasiment tout ce travail est converti en chaleur car les vitesses restent très faibles et l'énergie cinétique est négligeable!

Dans l'atmosphère, c'est un peu différent car les effets inertiels (énergie cinétique) ne peuvent pas être négligés et l'air est compressible. Les cellules de Hadley sont néanmoins une structure convective typique qui collecte la chaleur aux endroits chauds pour la redéposer aux endroits froids. Elles sont déclenchées par une instabilité verticale localisée aux basses latitudes mais, puisque l'air ne s'échappe pas de la troposhère, le panache s'étale horizontalement. Le mouvement vertical doit être compensé par des apports horizontaux à la base, ce qui est un peu compliqué par la force de Coriolis qui ne joue pas dans le manteau (vitesses trop faibles). Le premier paragraphe de la définition du dictionnaire décrit bien le caractère un peu abusif de la description météo qui est lié au très fort rapport de la dimension horizontale à l'épaisseur de l'atmosphère. Ce rapport permet de séparer nettement le transfert vertical du transfert horizontal. Le propre du jargon de spécialité est de raccourcir une acception de spécialiste mais cet usage sème la confusion lorsque l'on passe au manteau ou même à l'océan

Dans le passé, on utilisait indifféremment le terme de mouvement advectif et de mouvement convectif pour désigner le mouvement du milieu dans son ensemble. Si l'on réserve le terme de convection aux mouvements provoqués par la poussée d'Archimède, on exclut ceux provoqués par d'autres causes: tout le monde sait qu'un convecteur mural n'a pas de ventilateur. Le qualificatif de "naturelle" pour ce type de convection tombe progressivement en désuétude. A proximité d'un ventilateur, dans un tuyau d'arrosage sous pression, on parlait autrefois de convection forcée, ce que l'usage moderne a remplacé par le terme général d'advection. L'advection est donc le transport d'une quantité additive (la chaleur, l'énergie interne, un élément chimique arbitraire, les charges électriques) par le mouvement du milieu, quelle que soit l'origine de ce mouvement (instabilité gravitaire ou entraînement forcé).

La vitesse de l'advection est donc la vitesse locale de la matière. Le flux advectif est le contenu en chaleur de la masse transportée par le matériel advecté par unité de temps*, c'est à dire le produit de la vitesse d'advection par le contenu en chaleur de l'élément de volume. Le flux conductif de chaleur est indépendant du mouvement: il est proportionnel au gradient de température (loi de Fourier ou, pour la diffusion la loi de Fick). Le flux total de chaleur est la somme du flux conductif et du flux advectif. J'ai ignoré bien sûr partout le transfert radiatif.

* Je trouve très lumineuse l'idée simple que la vitesse est le flux advectif de volume, ce qui se démontre aisément : le flux de masse devient le flux de volume fois la masse volumique, le flux advectif de chaleur devient le flux de masse fois la quantité de chaleur par unité de masse, etc.