Article | 22/03/2019
La Terre aplatie : le théorème de Clairaut
22/03/2019
Résumé
Après le calcul de Newton pour une Terre ellipsoïdale homogène en rotation axiale, Clairaut résout le calcul de l'aplatissement pour une Terre plus réaliste, stratifiée en couches de densités différentes, grâce à un système d'équations toujours utilisées de nos jours.
Table des matières
Transcription par Daphné Lemasquerier et Frédéric Chambat de la présentation de Frédéric Chambat du 12 octobre 2015 à l'ENS de Lyon, donnée dans le cadre du cours pluridisciplinaire des écoles doctorales EPIC, PHAST et INFOMATH intitulé La Terre, sa forme, sa rotation, ses marées - Morceaux choisis mathématiques, géophysiques et historiques.
Avertissement
Cet article est très calculatoire et rebutera à priori un lecteur peu habitué aux gradients, laplaciens et autres fonctions harmoniques, même si le raisonnement suivi reste compréhensible à qui ne peut refaire les calculs. Ce sont sans doute les esprits plus “physiciens” qui apprécieront le plus ce développement explicite des équations de Clairaut.
Newton avait su faire en 1687 le calcul de l'aplatissement ε d'une Terre en rotation axiale supposée homogène et ellipsoïdale de révolution, en fonction du petit nombre sans dimension m qui représente la force centrifuge à l'équateur normalisée par la gravité moyenne (cf. La Terre est un peu aplatie : comment Newton calcule l’aplatissement « sans sortir de chez lui »). Il trouvait . En 1743, Clairaut a résolu le problème équivalent plus ardu pour une Terre stratifiée en couches de densités différentes. Il trouve alors que ε = Cm où C est une constante qui dépend de la stratification en densité ρ(r). C'est ce calcul qui est présenté ici. Il débouche sur diverses équations de Clairaut, toujours utilisées de nos jours.
Forme d'une Terre non homogène en équilibre hydrostatique et en rotation autour de l'axe des pôles ?
L'équilibre hydrostatique auto-gravitant répond à deux équations. La première fait intervenir l'équilibre entre la pression p et la pesanteur , où W est le potentiel de pesanteur. La seconde est connexe au théorème de Gauss et relie W à la densité ρ et à la vitesse angulaire de rotation de la Terre ω :
- ;
- (éq. 1)[1]
La première relation est possible si le terme de droite est bien un gradient (auquel cas, elle sert à déterminer la pression). Pour que ce soit le cas, il faut et il suffit que le rotationnel du second membre soit nul, en notant ∧ le produit vectoriel, les formules classiques des opérateurs différentiels montrent que cela revient à :
- .
Cette relation montre que les surfaces de potentiel de pesanteur constant doivent être des surfaces de densité constante (isopycnes). On peut aussi montrer que les interfaces, ainsi que les surfaces d'équipression, doivent être de telles surfaces équipotentielles et isopycnes (la surface d'un lac au repos, par exemple, est une équipression, une équipotentielle et une isopycne).
On ne sait pas résoudre ces relations en toute généralité (numériquement, on sait peut-être). C'est-à-dire qu'on ne sait pas quelles sont toutes les formes d'équilibre possibles d'une planète en rotation. Dans le cas où la rotation est peu rapide, c'est-à-dire où le paramètre m est petit (force centrifuge à l'équateur faible devant la gravité), on utilise une technique de perturbation au voisinage de la configuration sphérique : on suppose que la Terre est proche de la symétrie sphérique. La configuration sphérique (dite de référence) de la Terre est alors définie comme étant une moyenne latérale de la Terre aplatie. Elle est caractérisée par l'équilibre sans rotation (ω=0) et on désigne par l'indice 0 cette configuration de référence sphérique :
- ;
- (éq. 2)
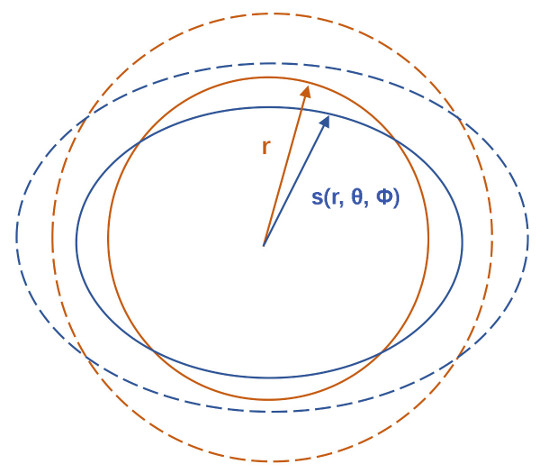
Le fait que la Terre soit supposée proche de la symétrie sphérique, revient à dire que la distance au centre s d'une surface équipotentielle de pesanteur est supposée proche de son rayon moyen r (figure 2). On définit alors h, δω et δr comme de petites variations par rapport à la configuration de référence sphérique :
- s(r,θ,Φ) = r + h(r,θ,Φ) avec h ≪ r ;
- W(r,θ,Φ) = W0(r) + δW(r,θ,Φ) avec δW ≪ W0 ;
- ρ(r,θ,Φ) = ρ0(r) + δρ(r,θ,Φ) avec δρ ≪ ρ0 (éq. 3)
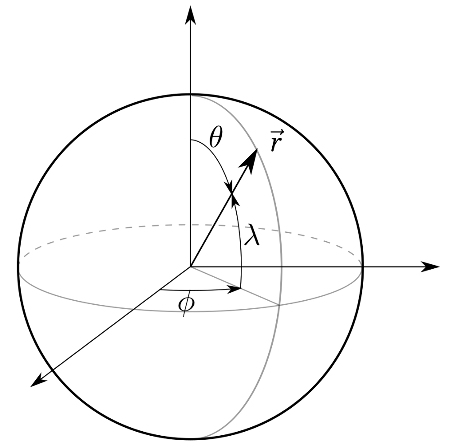
avec r, θ et Φ les 3 variables du repère sphérique (figure 1).
Figure 1. Repère sphérique
r ∈ [0, +∞[ est le rayon, Φ ∈ [0, 2π] la longitude, et θ ∈ [0, π] la colatitude ( λ = π/2 − θ est la latitude).
Le fait que la densité sur une sphère de rayon r est choisie égale à celle sur la surface déformée correspondante s'écrit ρ(s,θ,Φ) = ρ0(r), c'est-à-dire ρ(r+h,θ,Φ) = ρ0(r+h,θ,Φ) + δρ(r+h,θ,Φ) = ρ0(r). D'autre part, un développement au premier ordre en h/r donne : ρ0(r+h) ≈ ρ0(r) + (∂ρ0/∂r)h. En notant avec un point la dérivée radiale, on obtient alors tout compte fait :
- (éq. 4)
Le fait que les surfaces considérées sont des équipotentielles s'écrit quant à lui : W(s,θ,Φ) = W0(r) + C(r). En procédant de la même manière que précédemment et en utilisant , on obtient alors :
- (éq. 5)
En soustrayant les équations 1 et 2, on a par ailleurs . En injectant dans cette relation les équations 4 et 5 et en choisissant C de façon à ce que son laplacien soit 2ω2 (C est donc la partie sphérique du potentiel centrifuge), on obtient une équation aux dérivées partielles vérifiée par h :
- (éq. 6)
Dans cette équation, on se donne ρ0(r) qui permet de calculer g0(r). On veut alors déterminer h(r,θ,Φ). Deux conditions aux limites sont nécessaires. Au centre, il ne faut pas qu'il y ait de trou ; il faut donc que les surfaces s(r,θ,Φ) = cste puissent converger jusqu'au centre, ce qui s'exprime par s(0,θ,Φ) = 0, soit h(0,θ,Φ) = 0, ∀ (θ,Φ). À l'extérieur, le potentiel vérifie . Il faut que ce potentiel et son gradient soient les mêmes que le potentiel interne et son gradient à la surface de la Terre (r=R) : cela donne une condition supplémentaire sur le potentiel interne, qui dépend de ω.
Pour résoudre ces équations, on utilise classiquement la séparation des variables, et pour cela on projette h(r,θ,Φ) sur une base de fonctions qui ne dépend que des variables angulaires θ et Φ, ce sont les fonctions harmoniques sphériques.
Les fonctions harmoniques sphériques
Les harmoniques sphériques sont l'équivalent des séries de Fourier[2] sur la sphère : elles s'appliquent à une fonction des deux variables θ et Φ du repère sphérique (figure 1). Leur propriété est que toute fonction f(θ,Φ) peut se décomposer sous la forme :
où l est le degré de l'harmonique, m est l'ordre, sont les coefficients du développement, et sont les fonctions harmoniques sphériques qui forment ainsi une base des fonctions définies sur la sphère.
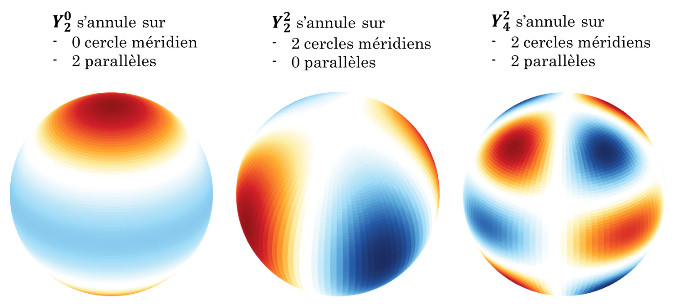
Les sont des fonctions qui oscillent en θ et en Φ. Elles s'annulent sur m cercles méridiens, et l−m parallèles (figure 3). Par exemple, pour représenter une Terre aplatie aux pôles, on utilise , qui s'annule uniquement sur deux parallèles :
- .
Figure 3. Exemples d'harmoniques sphériques
La couleur indique la valeur de la fonction : rouge pour les valeur positives, bleu pour les valeurs négatives, blanc pour les valeurs nulles.
Indiquons aussi que la première harmonique est constante : . Outre le fait que ces fonctions forment une base, une propriété essentielle est qu'elles sont des fonctions propres du laplacien :
- (éq 7)
Résolution des équations
Décomposons h grâce aux harmoniques sphériques :
- .
En injectant cette expression dans l'équation 6, puis en utilisant l'équation 7 et la propriété :
- ,
on voit que l'équation 6 s'écrit sous la forme :
- ,
avec a, b et cl des fonctions connues de ρ0(r) et g0(r) mais que nous n'explicitons pas. cl dépend, de plus, de l.
Comme les forment une base, il vient :
- (éq. 8)
Le cas l = 0 définit juste la sphère par rapport à laquelle on mesure la hauteur h. En choisissant par convention la sphère qui a le même rayon moyen que la Terre déformée, on a la solution identiquement nulle (cela provient aussi du choix de C). On ne s'intéressera plus maintenant qu'au cas l ≠ 0.
En harmoniques sphériques, la condition au centre s'écrit bien entendu :
- (éq. 9)
Pour la condition au bord, il faut procéder à un certain nombre de calculs que nous ne détaillons pas ici[3], et qui donnent :
- ;
- (éq. 10)
On remarque que pour (l,m) ≠ (2,0), le système (équation et conditions aux limites) est complètement homogène : la fonction nulle, h = 0, est solution évidente. Poincaré (1902) a montré que c'était la seule solution, quel que soit la densité ρ0(r), pour autant qu'elle décroisse avec le rayon.
La solution générale contient donc un seul terme, en (l,m) = (2,0) :
- .
Physiquement, cela provient du fait que le potentiel de rotation est une somme de deux harmoniques sphériques uniquement, l'harmonique l = 0 et l'harmonique (l, m) = (2,0).
La forme de la Terre est donc connue : . C'est à peu près un ellipsoïde de révolution autour de l'axe de rotation. Il reste à déterminer h(r) ou, ce qui est équivalent, son aplatissement. Ce dernier est défini par la différence relative entre l'axe équatorial et l'axe polaire :
- .
En introduisant cette nouvelle variable à la place de h, on obtient un nouveau système d'équation. On introduit aussi , la densité moyenne dans la sphère de rayon r, qu'on peut définir par :
- .
La condition au centre (équation 9) n'est pas immédiate à transformer. Disons juste que pour la trouver, il faut faire un développement en série de r au voisinage du centre. Tous comptes faits, les équations 8, 9 et 10 deviennent :
- ;
- ;
- (« équations de Clairaut »)
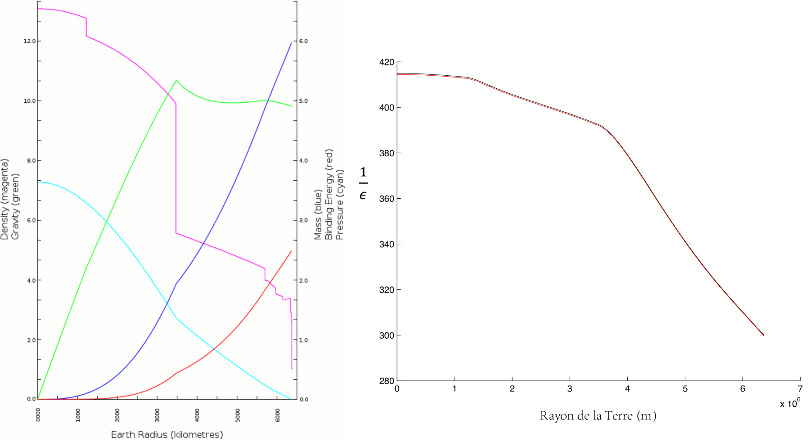
Il s'agit du système des « équations de Clairaut », permettant de déterminer l'aplatissement des ellipses à tout rayon. Connaissant ρ0(r) à partir d'un modèle moyen de Terre comme le modèle PREM, et la vitesse angulaire de rotation de la Terre ω, on est donc capable de résoudre numériquement cette équation différentielle, et d'en déduire la forme de la Terre non homogène et hydrostatique. La figure 4 donne par exemple l'évolution de 1/ε obtenue par résolution de ce système à partir de la densité du modèle PREM. L'aplatissement calculé de la Terre est de l'ordre de 1/300 en surface et de 1/415 au centre. On peut améliorer ce calcul en le faisant au deuxième ordre en ε (cf. Chambat et al., 2010 [1]), et au troisième ordre pour certaines planètes naines (cf. Rambaux et al., 2015 [3]). On trouve alors environ 1/299 pour l'aplatissement en surface, très proche de l'observé, qui est 1/298,25. La Terre est donc très proche de l'équilibre hydrostatique. Grâce au calcul de Clairaut, on sait corriger de l'effet d'ellipticité les observations gravimétriques, sismologiques, etc.
Figure 4. Calcul de l'aplatissement ε par les équations de Clairaut appliquées au modèle PREM
À gauche : densité (rose, en g/cm3), gravité (vert, en m/s2), masse (bleu, en 1024 kg), pression (cyan, en 1011 Pa) et énergie gravitationnelle (rouge) déduits du modèle PREM.
À droite : évolution de l'inverse de l'aplatissement en fonction du rayon, déterminée en injectant le modèle PREM dans l'équation différentielle en ε. L'aplatissement est minimal au centre de la Terre.
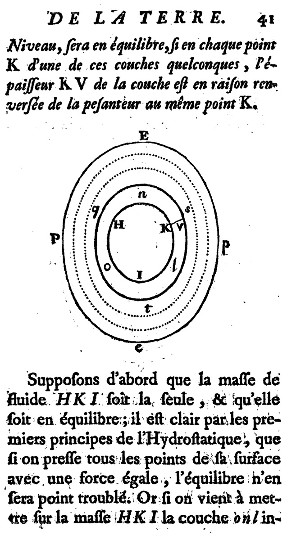
Terminons par un hommage à Clairaut. Sa Théorie de la figure de la Terre [2] (1743) est une œuvre majeure de l'hydrostatique et probablement la plus importante sur la forme de la Terre (figures 5 à 8). On trouvera des informations de qualité sur Clairaut, et en grande quantité, sur l'extraordinaire site clairaut.com, réalisé par Olivier Courcelle. On pourra visionner quelques exposés filmés à l'occasion du tricentenaire de Clairaut (2013) sur le site de l'Académie des sciences.
Bibliographie
F. Chambat, Y. Ricard, B. Valette, 2010. Flattening of the Earth: further from hydrostaticity than previously estimated, Geophysical Journal International, 183, 727-732 [pdf]
A.C. Clairaut, 1743. Théorie de la figure de la terre tirée des principes de l'hydrostatique, David Fils, Paris, 351p
N. Rambaux, F. Chambat, J.C. Castillo-Rogez, 2015. Third-order development of shape, gravity, and moment of inertia for highly flattened celestial bodies. Application to Ceres, Astronomy & Astrophysics, 584, A127 [pdf]
[1] Le gradient est la dérivée première en 3D : . Le laplacien, noté ∆ ou ∇2, est la somme des dérivées secondes : .
[2] Une fonction f définie sur un cercle (= périodique de période 2π) peut s'écrire sous la forme , c'est-à-dire qu'elle se développe en une série de sinusoïdes, qu'on appelle développement en série de Fourier.
[3] Il faut écrire que le potentiel de pesanteur est la somme du potentiel centrifuge dont on connait la forme, et du potentiel de gravité, qui est harmonique (son laplacien est nul) et dont on connait donc la forme en harmoniques sphériques. En écrivant la continuité, au bord r = R, du potentiel et de son gradient, on obtient ainsi la condition.