Le compactage dynamique, une méthode pour construire sur des alluvions meubles

Source - © 2014 Pierre Thomas

Figure 1. Série de 6 images prises tous les 1/3 de seconde montrant la chute d'une masse d'acier de 12 tonnes, d'un diamètre de 2m et tombant d'une hauteur d'environ 15 m (un immeuble de 5 étages)

En arrivant à terre, cette masse tasse le sol, ce qui le rendra plus compact, et plus apte à supporter une construction.

Cette série de photos a été prise en juillet 2014 sur un chantier situé à Villard-Bonnot (Isère) et destiné à accueillir un entrepôt. Le tassement du sol était effectué par l'entreprise Ménard spécialisée en géotechnique. Au fond, le Mont Saint Eynard, dont le sommet est constitué de calcaire tithonique et d'où a été prise la photo de la figure 18.

Source - © 2014 Pierre Thomas Figure 2. Une des deux grues et une des 3 masses chargées d'effectuer le tassement du sol sur le chantier de Villard-Bonnot (Isère) en juillet 2014 La grue mesure 25 m de hauteur ; la masse de 12 tonnes mesure 2 m de côté pour 40 cm d'épaisseur.	Source - © 2014 Pierre Thomas Figure 3. Gros plan sur la masse de 12 tonnes de dimensions environ 0,4 x 2 x 2 m
Source - © 2014 Pierre Thomas Figure 4. Instantané montrant la masse de 12 tonnes arrivant au sol	Source - © 2014 Pierre Thomas Figure 5. Empreinte de la chute de la masse de 12 tonnes après un choc unique sur un sol déjà pré-compacté

Construire sur des argiles et/ou des alluvions sableuses plus ou moins gorgées d'eau est très problématique. La Tour de Pise, bâtie sur les alluvions de l'Arno le rappelle. Sans vouloir rivaliser avec ce célèbre monument, un entrepôt est en construction à Villard-Bonnot (banlieue NE de Grenoble, Isère) sur les alluvions récentes de l'Isère. Comment faire en sorte que cette construction soit stable ? Plusieurs solutions sont possibles, qui dépendent entre autres de l'épaisseur et de la nature des terrains meubles, et de la nature et du poids de la construction. Le compactage dynamique est l'une de ces solutions, choisie par le constructeur de l'entrepôt. Pour cela, il a fait appel à une entreprise de géotechnique, en l'occurrence l'entreprise Ménard. Le compactage dynamique consiste à tasser le sol en faisant tomber d'une grande hauteur, sur toute la surface à compacter, une masse très lourde. Il existe plusieurs variantes de cette technique, entre deux modes opératoires extrêmes. Le premier mode opératoire, celui illustré sur les images qui précèdent, consiste simplement à faire tomber une ou plusieurs fois une masse sur l'ensemble de la surface à compacter. La dépression engendrée par une première chute peut être comblée par des alluvions locales avant les chutes suivantes. Le deuxième mode opératoire est plus complexe. On fait d'abord un trou à la pelleteuse, et on le remplit avec des granulats (de quelques centimètres de diamètre) de roche dure (du calcaire urgonien venant des de carrières de l'Ouest grenoblois dans le cas de ce chantier). On fait tomber une ou plusieurs fois la masse, ce qui tasse et enfonce ces granulats durs dans le sous-sol meuble, ce qui laisse un trou. On remplit à nouveau ce trou de granulats, et on recommence autant de fois qu'il le faut. Toutes les combinaisons de ces deux modes opératoires sont possibles. Dans le cas du futur entrepôt de Villard-Bonnot, environ 400 points seront compactés avec le deuxième mode opératoire. C'est sur ces sites les plus compactés que seront bâtis les piliers et autres points d'ancrage qui devront supporter la charge la plus importante due au futur entrepôt. Entre ces futurs points d'ancrage, le compactage sera plus simple, fait avec le premier mode opératoire. Une fois connu le cahier des charges du constructeur, le choix de la méthode de stabilisation, le mode opératoire du compactage, le nombre et l'emplacement des points d'ancrage très compactés… tout cela doit être déterminé par le géologue de l'entreprise de géotechnique. Ces choix auront été précédés d'études ponctuelles de tassement, de plusieurs forages de reconnaissance de plusieurs mètres de profondeur…

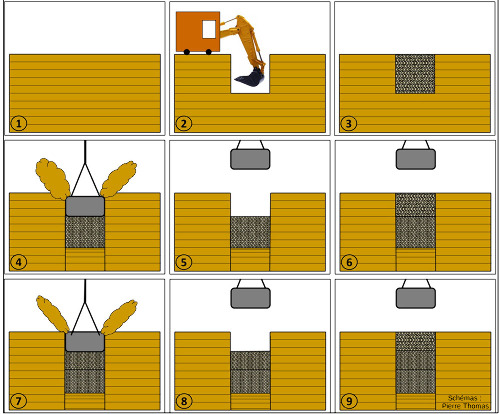
Source - © 2014 Pierre Thomas

Figure 9. Schéma résumant le deuxième mode opératoire de compactage, celui qui donne les points d'ancrage les plus aptes à supporter de fortes charges

On fait d'abord un trou à la pelleteuse (2), et on le remplit avec des granulats (de quelques cm de diamètre) de roche dure, ici, du calcaire urgonien venant des de carrières de l'Ouest grenoblois pour ce chantier (3). On fait tomber une ou plusieurs fois la masse, ce qui tasse et enfonce ces granulats durs dans le sous-sol meuble, ce qui laisse un trou (4 et 5). On remplit à nouveau ce trou de granulats (6), et on recommence autant de fois qu'il le faut (7, 8 et 9).

Source - © 2014 Pierre Thomas Figure 10. Une masse plus lourde (19 tonnes) et plus "étroite" (1,5 m de "diamètre") La chute d'une telle masse provoque une pression dynamique beaucoup plus importante que celle provoquée par les chutes des figures précédentes, et cela compacte le sous-sol meuble d'une manière beaucoup plus efficace.	Source - © 2014 Pierre Thomas / Olivier Dequincey pour Planet-Terre - ENS de Lyon Source - © 2014 Pierre Thomas Figure 11. Vidéo de la chute d'une masse de 19 tonnes
Source - © 2014 Pierre Thomas Figure 12. La masse de 19 tonnes juste après une chute	Source - © 2014 Pierre Thomas Figure 13. Trou laissé par une chute de la masse de 19 tonnes, qui vient d'être relevée et légèrement déplacée Emmanuel Javelaud donne l'échelle.

Source - © 2014 Pierre Thomas Figure 14. Tranchée faite sur le chantier de Villard-Bonnot Le sous-sol est composé d'argiles sableuses non consolidées déposées là par les crues de l'Isère	Source - © 2014 Pierre Thomas Figure 15. Paroi d'une tranchée faite sur le chantier de Villard-Bonnot Le sous-sol est composé d'argiles sableuses non consolidées déposées là par les crues de l'Isère
Source - © 2014 Pierre Thomas Figure 16. Détail de la paroi d'une tranchée faite sur le chantier de Villard-Bonnot Le sous-sol est composé d'argiles sableuses non consolidées déposées là par les crues de l'Isère

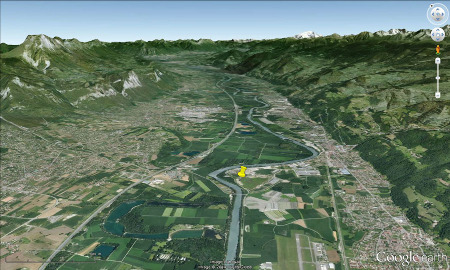Source - © 2014 Pierre Thomas Figure 17. Contexte géologico-morphologique du futur entrepôt (punaise jaune) de Villard-Bonnot au NE de l'agglomération grenobloise (Isère) Le chantier est situé juste à côté de l'Isère, rivière alpine qui a rempli sa vallée d'alluvions meubles. Bâtie dans le lit majeur de l'Isère, la zone du futur entrepôt est inondable, et l'entrepôt devra être surélevé pour être à l'abri des inondations. À gauche, le massif de la Chartreuse, avec la Dent de Crolles. À droite, le massif de Belledonne. Entre les deux, la vallée du Grésivaudan. Au fond légèrement à droite, le Mont Blanc.

Source - © 2014 Pierre Thomas Figure 18. La vallée du Grésivaudan vue du sommet du Mont Saint Eynard, juste au-dessus de Grenoble La flèche indique la localisation approximative du chantier de Villard-Bonnot.

En classe de Terminale (en 1969, il est vrai), le professeur de physique démontrait aux élèves (qui devaient le comprendre et l'apprendre) que la distance verticale z parcourue pendant un temps t par un corps en chute libre soumis à une seule force, son poids, lui-même dû à une accélération constante, la gravité terrestre, pouvait s'écrire de la manière suivant : $z=\frac{1}{2}.g.t^2$.

C'est en 1602 que Galilée a démontré expérimentalement cette relation (la distance parcourue par un corps en chute libre est indépendante de sa masse et varie comme le carré du temps de chute), après, dit-on, des observations qualitatives menées depuis le haut de la Tour de Pise. Il a quantifié ses observations de Pise, sans chronomètre précis, sans caméra ou appareil photo, mais avec d'élégants dispositifs expérimentaux dont certains sont conservés au Museo Galileo de Florence (Italie). La chute d'une masse de 12 tonnes sur une hauteur d'une vingtaine de mètres est suffisamment brève pour qu'on puisse considérer la résistance de l'air comme négligeable. On est donc dans les conditions proposées par Galilée. Les appareils photographiques modernes permettent de prendre des images en rafale (3 images/seconde dans le cas de mon appareil). Si on juxtapose régulièrement des photos de la chute de la masse de 12 tonnes, on peut voir si la distance parcourue est proportionnelle au temps (vitesse constante), au carré du temps… Si la distance parcourue était proportionnelle au temps, le centre de la masse décrirait un segment de droite sur la juxtaposition de photographies. Si la distance parcourue était proportionnel au carré du temps comme le prétendait Galilée, le centre de la masse décrirait un fragment de parabole sur la juxtaposition de photos. L'expérience faite en 2014 reproduit bien la loi énoncée par Galilée en 1602.

Source - © 2014 Pierre Thomas

Figure 19. Le "dispositif expérimental" utilisé pour redémontrer (à Villard-Bonnot en 2014) les lois de la chute des corps énoncées par Galilée en 1602

Au fond, le synclinal perché d'Urgonien de la Dent de Crolles.

Source - © 2014 Pierre Thomas

Figure 20. Lois de Galilée redémontrées à Villard-Bonnot…

Cette figure montre la juxtaposition régulière de six photos prises tous les 1/3 de seconde pendant la chute de la masse de 12 tonnes. Les centres des masses sur chacune des six photos ont été reliés par une ligne rouge. Si la distance parcourue était proportionnelle au temps, la ligne rouge serait un segment de droite. Si, comme le propose Galilée, la distance parcourue était proportionnelle au carré du temps, la ligne rouge dessinerait une courbe $z=\frac{1}{2}.g.t^2$, et serait un fragment de parabole. La ligne effectivement obtenue ressemble à un fragment de parabole. Il semble donc bien que Galilée avait raison !