Article | 15/06/2001
La forme de la Terre : plate, oblongue ou aplatie aux pôles ?
15/06/2001
Résumé
Évolution historique des idées à propos de la forme et de la taille de la Terre.
Table des matières
- La Terre sphérique des Anciens
- Le globe terraqué
- La triangulation géodésique
- Oblongue ou aplatie ?
- Les explications de l'aplatissement du globe
- De quelle "figure de la Terre" parle-t-on ?
- Nouvelle contradiction entre théorie et mesures géodésiques
- Des déterminations toujours plus précises et des explications nouvelles
- Bibliographie
- Citations
Tout au long de l'histoire, la figure de la Terre a intrigué, questionné. Comment connaître la forme d'une planète à laquelle on est pieds et poings liés ? La Terre a-t-elle à grande échelle une figure régulière ? Celle-ci est-elle la même que celle que prendrait une masse fluide ? Comment la Terre solide a-t-elle pu acquérir une figure d'équilibre ?
La Terre sphérique des Anciens
Dès le VIième siècle av. J.-C., les philosophes grecs, qui ne connaissent que le pourtour de la Méditerranée, s'interrogent sur la forme et l'étendue de leur promontoire : qu'y a-t-il derrière ce que l'on voit ? Jusqu'où s'étend la Terre ?
La Terre est supposée plate, de la forme d'un disque, entièrement ceinturée par le fleuve Océan et recouverte d'un ciel en coupole hémi-sphérique. L'hémi-sphéricité est suggérée par le mouvement des astres qui décrivent de grands arcs de cercles au cours de la journée et de la nuit. Le retour journalier de mouvements similaires pose question. Certains pensent que les astres, après avoir disparu de l'horizon, reviennent à leur point de départ en empruntant le fleuve Océan. D'autres avancent que ce sont chaque jour de nouveaux astres qui se déplacent dans le ciel, certaines parties de la Terre ayant le pouvoir de les allumer ou de les éteindre.
Quel support pour la Terre ?
Sur quoi s'appuie la Terre pour ne pas tomber vers un autre lieu du ciel ? L'interrogation est déroutante. Après l'avoir imaginé soutenue par un pilier imaginaire, Thalès (VIième siècle av. J.-C.) fait reposer la Terre sur de l'eau -les mouvements de l'eau sont la cause des tremblements de terre- et Anaximène (VIième siècle av. J.-C.) sur de l'air.
Anaximandre (VIième siècle av. J.-C.) rompt avec ces idées et le premier, par un défi de la pensée, il ose concevoir une Terre isolée, privée de tout appui, en équilibre au centre d'un ciel entièrement sphérique. Les astres peuvent maintenant passer sous la Terre et recommencer chaque jour leur course céleste sans jamais l'interrompre. La Terre reste éternellement au repos puisqu'elle n'a plus aucune raison de se diriger vers un lieu du ciel plutôt qu'un autre, toutes les directions se valant. Elle a, selon Anaximandre, la forme d'un cylindre, telle une colonne de pierre tronquée, dont seule la face supérieure est habitée.
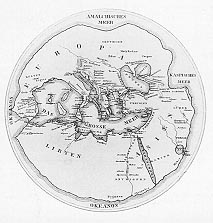
Figure 1. Carte d'Hécatée de Milet (VIe siècle av. J.-C.)
Carte reconstituée par des historiens allemands.
Et la Terre devint ronde...
Parménide (v. 515-450 av. J.-C.), qui se rattache à l'école pythagoricienne (Pythagore, v. 560-480 av. J.-C.), poursuit les réflexions d'Anaximandre et suppose que la Terre est sphérique. Ses motivations semblent essentiellement d'ordre esthétique et géométrique et reposent sur des considérations de symétrie entre la Terre et le ciel sphérique qui l'enveloppe. Pour que l'ensemble Terre-ciel soit de symétrie parfaite, ne faut-il pas que la Terre soit elle-même de forme sphérique ?
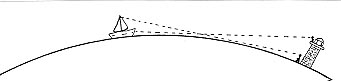
La rotondité de la Terre s'impose face à l'image du disque au IVe siècle av. J.-C., entre Platon (v. 428-348 av. J.-C.) et Aristote (v. 384-322 av. J.-C.). Platon prouve la sphéricité en donnant deux indices : la forme des éclipses de Lune qui montre que l'ombre projetée de la Terre est toujours circulaire (Figure 2) et le changement dans la configuration des cieux étoilés (hauteur des étoiles sur l'horizon) lors des déplacements en latitude qui s'expliquent par la courbure de la Terre faisant obstacle à une vision complète du ciel (Figure 3). Plus tard, un troisième indice est rapporté par Strabon (v. 58 av. J.-C.- 23 apr. J.-C.) : lorsqu'un bateau s'éloigne d'un port, sa coque, progressivement masquée par l'horizon (la courbure de la Terre), disparaît avant son mât (Figure 4).
Figure 3. Courbure de la Terre indiquée par l'observation des étoiles En deux lieux différents du globe, la direction d'une étoile ne fait pas le même angle avec la verticale. | Figure 4. Courbure de la Terre indiquée par l'observation d'un bateau s'éloignant du port Lorsqu'un bateau s'éloigne au large, sa coque disparaît avant son mât... |
Aristote donne également une explication physique à la rotondité de la Terre. Chaque portion d'élément terre qui constitue la planète possède une tendance à se mouvoir vers le centre de la Terre. Cette chute provoque une agglomération des différentes parties, tassement et compression, et impose que le volume total soit approximativement semblable sur chaque côté, autrement dit que la Terre ait sensiblement la forme régulière et symétrique de la sphère. C'est la première apparition de la notion de figure d'équilibre.
Les premières mesures de la circonférence terrestre
Reconnaître la sphéricité de la Terre est une chose, mais encore faut-il en déterminer le rayon... Eudoxe (v. 400-355 av. J.-C.) développe la géographie mathématique et met au point trois méthodes pour déterminer la latitude d'un lieu : l'observation de la hauteur du pôle céleste sur l'horizon, l'observation de la hauteur méridienne des étoiles ou du Soleil, et le rapport entre la durée du jour le plus long de l'année et celle du jour le plus court. C'est en établissant l'écart de latitude entre deux lieux situés sur un même méridien et en estimant la distance que les sépare, qu'Eudoxe peut donner la première valeur de la circonférence terrestre rapportée par Aristote.
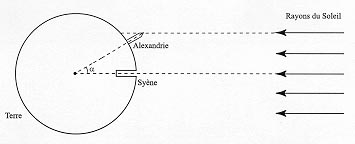
C'est cependant Eratosthène (284-192 av. J.-C.) qui est connu pour avoir donné la première estimation précise de la circonférence terrestre en se servant de la différence de hauteur du Soleil le jour du solstice d'été (Figure 5).
Eratosthène sait qu'à Syène -aujourd'hui Assouan en Egypte-, le jour du solstice d'été, à midi, les rayons solaires tombent verticalement par rapport au sol et éclairent un puit jusqu'à son fond. Au même moment à Alexandrie, ville située à peu près sur le même méridien mais plus au nord, le Soleil n'est déjà plus au zénith. La longueur de l'ombre d'un obélisque permet de connaître l'angle que fait la direction du Soleil avec la verticale du lieu et par là même de déterminer celui que fait les deux villes à partir du centre de la Terre. Pour en déduire la valeur de toute la circonférence terrestre, il "suffit" à Eratosthène d'estimer la distance séparant les deux villes en comptant le nombre de pas effectué lorsqu'on relie les deux villes à la marche !
Poseidonios (v. 135-50 av. J.-C.) fait une nouvelle mesure au Ier siècle av. J.-C. Il note que dans l'île de Rhodes l'étoile Canopus ne fait que frôler l'horizon alors qu'elle atteint une hauteur méridienne de 7°30' à Alexandrie située très approximativement sur le même méridien. Il lui suffit là encore d'estimer la distance entre Rhodes et l'Egypte en se servant du temps de navigation des bateaux pour connaître la circonférence du globe.
Si la latitude des lieux peut être connue assez facilement, la détermination des longitudes est bien plus délicate : elle s'effectue à partir de l'estimation des distances (comptabilisation des jours de marche ou de navigation) converties en mesures angulaires. Hipparque de Nicée (IIe siècle av. J.-C.) montre que l'observation simultanée des éclipses de Lune en des lieux différents donne une méthode plus rigoureuse. L'éclipse survient en effet au même moment absolu qui correspond à des heures locales différentes. Le décalage de temps représente en heures les écarts de longitudes. Ces observations sont cependant rares et de médiocre qualité.
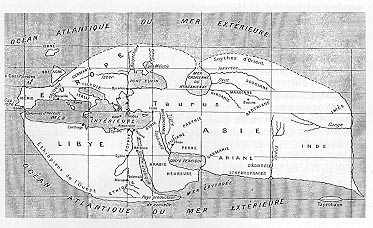
Figure 6. Carte du monde par Strabon
La carte du monde connu de Strabon (Figure 6), inspiré de celle d'Eratosthène (IIIe siècle av. J.-C.). Eratosthène utilise deux axes origines, l'un pour les latitudes (le parallèle de 36° de latitude nord qui passe par Gibraltar, le détroit de Sicile et Rhodes) et l'autre pour les longitudes (le méridien passant par Rhodes). Le monde connu ne couvre pas un quart de la surface du globe. Qu'est-ce qui occupe les autres quartiers du globe ? (in G. Aujac, Strabon et la science de son temps, Paris, Les Belles Lettres, 1966, p.341)
Les choses en restent là durant des siècles, malgré quelques nouvelles tentatives d'évaluation de la circonférence de la part des astronomes arabes.
Le globe terraqué
Le monde habité est-il une île unique ou les autres quartiers du globe possèdent-ils également des terres émergées ? La question se pose encore aux savants occidentaux du XIVe siècle puisqu'à leur époque les trois quarts de la surface terrestre restent inexplorés. Une question plus lancinante se dessine en creux : sommes-nous les seuls habitants de la Terre ?
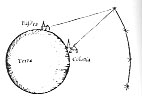
Jean Buridan (1300-1358) considère que la terre et l'eau forment deux sphères de centres distincts : la terre domine la mer sur un seul quartier du monde où la vie a pu être abritée et est entièrement recouverte dans les autres (Figure 7). Cette situation provient de l'hétérogénéité de la Terre qui est plus légère du côté exposé au Soleil et plus dense du côté immergé. Le centre de pesanteur est donc différent du centre de grandeur de la sphère de terre. Or c'est autour du premier que s'arrange l'eau qui se décale ainsi par rapport à la terre. Le raisonnement est cohérent et la vison de la Terre bien différente de celle que l'on peut avoir aujourd'hui.
Figure 7. Les sphères d'eau et de terre de Buridan
La découverte de l'Amérique par Christophe Colomb (1450-1506) en 1492, puis les explorations maritimes de Vasco de Gama (1469-1524), de Vespucci (1454-1512) et de Magellan (1480-1521) montrent que la thèse de Buridan est fausse : les océans ne font que combler les dépressions les plus profondes de la surface, et dans toutes les parties du monde, il existe des terres émergées et des habitants. La terre et l'eau ne forment donc qu'une seule et même sphère qui reçoit le nom de "globe terraqué", remplacé ensuite par "globe terrestre".
Kepler (1571-1630), en 1618, confirme ces propos. Il remarque judicieusement que les plus hautes montagnes ne sont jamais élevées de beaucoup au-dessus des mers et donc que la figure de la Terre solide est bien sensiblement la même que celle des eaux. À des chemins parcourus sur terre ou sur mer correspondent également toujours des degrés égaux dans le ciel, ce qui ne pourrait pas être le cas si la Terre n'était pas sphérique. Mais pourquoi donc la Terre solide est-elle être ronde et non beaucoup plus bosselée ? Soit elle a été crée d'emblée sphérique, soit elle était, à cause du feu ou de l'eau, dans un état initial fluide qui lui a permis de se laisser modeler librement par la gravité et d'acquérir sa forme ronde. La figure d'équilibre de la Terre imposerait donc une fluidité originelle. C'est la première interrogation sur l'état physique de la Terre au moment de sa formation.
La triangulation géodésique
En 1528, Jean-François Fernel (1497-1558), médecin d'Henri II, tente une nouvelle estimation de la circonférence terrestre. Reprenant la méthode d'Eratosthène, il s'éloigne de Paris vers le nord jusqu'à trouver une hauteur méridienne du Soleil plus faible de 1°. Il détermine alors la distance qui le sépare de Paris en comptant le nombre de tours de roue du coche qui le ramène vers la capitale ! Il obtient ainsi la première valeur du degré de méridien, 56 747 toises, soit environ 110 km (1 toise = 1,9490363 m).
Tant que la mesure des distances repose sur des étalons comme la longueur d'un pas de marcheur ou le périmètre d'une roue empruntant des routes qui n'ont rien de linéaires, on ne peut espérer des résultats qui ne soient autre chose que d'heureuses coïncidences.
Une nouvelle méthode voit cependant le jour, inventée par Frisius (1508-1555) en 1533. Elle consiste à relier les deux lieux d'un méridien dont on veut connaître la distance par une chaîne de triangles. Les sommets successifs des triangles sont bien marqués et visibles de proche en proche. En mesurant la longueur d'un côté de départ -la base- et l'ensemble des angles, on peut par trigonométrie établir la longueur de tous les côtés des triangles. Il reste à orienter le réseau de triangles par rapport au méridien pour connaître par projection la distance entre les deux lieux. La détermination de la différence de latitude se fait par l'observation de la distance zénithale d'une même étoile.
En 1589, l'astronome Tycho Brahé (1546-1601) utilise la triangulation pour relier l'île de Hven où est installé son observatoire à la côte danoise et Snellius (1580 ou 1591-1626) en 1615, s'en sert pour calculer la première méridienne au Pays-Bas. Sa mesure est entachée d'erreurs mais elle a le mérite de lancer la méthode.
C'est surtout l'abbé Picard (1620-1682) qui développe avec succès la triangulation géodésique en 1669-1670. L'arc qu'il entreprend de mesurer s'étend de Malvoisine (à 30 km au sud de Paris) jusqu'à Sourdon (à 20 km d'Amiens) et comprend treize triangles principaux. Grâce à une instrumentation perfectionnée par ses soins, il peut effectuer des mesures précises et obtient pour le degré du méridien une longueur de 57 060 toises, soit un peu plus de 111 km. Picard peut vraiment être considéré comme le père de la géodésie géométrique.
Oblongue ou aplatie ?
La Terre est-elle vraiment sphérique ? À peine la mesure de Picard effectuée que le doute s'insinue dans les esprits. En effet, en 1659 (son ouvrage est publié en 1673), Huygens (1629-1695) a découvert l'existence de la force centrifuge et donné son expression en v2/r. La force centrifuge qui naît de la rotation terrestre est nulle aux pôles et maximale à l'équateur ; elle agit différemment suivant la latitude. Ne peut-elle pas avoir un effet sur la forme de la Terre ? La question semble d'autant plus pertinente que J.-D. Cassini (1625-1712) a observé en 1666 que Jupiter a une figure aplatie (son rayon équatorial est supérieur à son rayon polaire).
Le point de vue des théoriciens
En 1671, Picard avance que la Terre n'est pas parfaitement sphérique. Vers 1675, Hooke (1635-1703) affirme que du fait de leur mouvement de rotation, toutes les planètes sont des ellipsoïdes aplatis. Il renchérit en 1686-1687 en expliquant que deux forces agissent à la surface de la Terre dans des directions différentes : la gravité qui est dirigée vers le centre de la planète et la force centrifuge qui est une force expulsive dirigée perpendiculairement à l'axe de rotation. La somme de la gravité et de la force centrifuge est nommée pesanteur. La forme de la surface des eaux de la Terre est ovale parce que la pesanteur est plus faible à l'équateur qu'aux pôles et que la force centrifuge tend à renfler les régions de basses latitudes aux dépens des régions polaires.
Newton (1642-1727) approfondit la question en 1687. Si la Terre n'avait pas son mouvement journalier, elle serait parfaitement sphérique à cause de l'égale gravité de ses parties. Mais du fait de sa rotation, elle prend une forme ellipsoïdale. Il précise son raisonnement : les mers, grâce leur mobilité, cèdent entièrement à la rotation diurne et ont immanquablement une figure aplatie ; mais puisque les terres émergées sont réparties uniformément à la surface du globe et ont à peu près partout la même altitude, la Terre solide doit avoir elle aussi une figure aplatie, identique à celle des eaux. On reconnaît le raisonnement de Kepler et comme ce dernier, Newton ajoute que ceci impose que la Terre solide ait été fluide à un moment donné de son histoire.
Figure 9. Isaac Newton (1642-1727)
Newton cherche à calculer l'aplatissement de la Terre en supposant qu'elle soit fluide et homogène et en utilisant sa théorie de l'attraction universelle en 1/r2. Il se sert d'un procédé astucieux : il considère que deux colonnes fluides partant l'une du pôle et l'autre de l'équateur et se rejoignant au centre de la Terre doivent se faire équilibre. L'égalité du poids des deux colonnes implique que la colonne rejoignant l'équateur, dont la pesanteur est diminuée par la force centrifuge, soit plus longue que celle rejoignant le pôle. Pour son calcul, il doit déterminer l'attraction au pôle et à l'équateur d'un ellipsoïde de révolution, et c'est la première fois que l'attraction d'un corps non-sphérique est calculée. Il trouve un aplatissement de 1/230 (Figure 10).
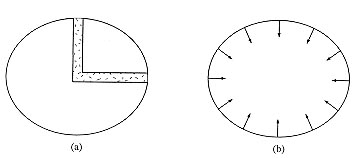 Figure 10. Modèle pour le calcul de l'aplatissement de la Terre selon Newton (a) et Huygens (b) Newton calcule l'aplatissement de la Terre en considérant que deux canaux partant l'un du pôle et l'autre de l'équateur et se rejoignant au centre se font équilibre (a) et Huygens en supposant que la surface est en tout point perpendiculaire à la pesanteur (somme de la gravité et de la force centrifuge). | 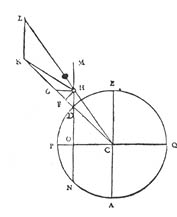 Figure 11. Force centrifuge révélée par Huygens Figure de Huygens montrant qu'un fil à plomb n'est pas dirigé vers le centre de la Terre car il est dévié par la force centrifuge. La figure est renversée de 90° par rapport à nos conventions actuelles : P et Q sont les pôles de rotation, KH représente une corde qui soutient un plomb H, qui s'écarte de la perpendiculaire KDC parce qu'il est rejeté par le mouvement de rotation suivant la ligne ODM. |
En 1690, Huygens (Figure 12) propose un autre calcul de l'aplatissement. Comme Hooke, il remarque d'abord qu'un fil à plomb qui donne la direction de la pesanteur (et donc de la verticale) n'est pas dirigé vers le centre de la Terre mais s'écarte vers l'équateur parce qu'il est rejeté par le mouvement de rotation (Figure 11). Il pose ensuite sa condition d'équilibre : la Terre, supposée fluide, garde une forme constante si sa surface est, en chacun de ses points, perpendiculaire à la direction de la pesanteur. Le lien entre forme de la Terre et direction de la pesanteur apparaît clairement (Figure 10).
Source - © Education in Physics and Mathematics - ZONA Land
Figure 12. Christian Huygens (1629-1695)
La différence fondamentale entre Newton et Huygens réside dans la conception de l'attraction. Huygens n'accepte pas l'attraction universelle, cet attraction à distance qui paraît par trop mystérieuse. Pour lui, la Terre baigne dans une matière subtile en rotation : l'éther. La gravité consiste en « l'effort que fait la matière fluide [l'éther], qui tourne circulairement autour du centre de la Terre en tous sens, à s'éloigner de ce centre, et à pousser en sa place les corps qui ne suivent pas ce mouvement ». Les corps tombent à la surface de la Terre parce qu'ils sont pressés et poussés par quelques autres corps. La gravité ne consiste pas en une attraction de masse à masse mais en une réaction au mouvement centrifuge de l'éther.
À grandes distances de la Terre, les lois d'attraction de Newton et de Huygens sont, d'un point de vue mathématique, strictement identiques : elles sont proportionnelle à la masse totale du globe et inversement proportionnelle au carré de la distance au centre. Elles diffèrent cependant dans le voisinage de la planète : alors que pour Huygens la forme du corps n'a aucune importance, elle est déterminante pour Newton qui affirme que l'attraction d'un ellipsoïde est différente de l'attraction d'une sphère (les masses s'éloignant de la répartition sphérique possèdent en effet une capacité d'attraction qui perturbe l'attraction de la sphère, cette perturbation est sensible lorsqu'on est proche de la Terre mais devient négligeable à grandes distances). Cette différence se retrouve dans le calcul de l'aplatissement : avec sa loi d'attraction restreinte, Huygens obtient une valeur de 1/578, plus faible que celle de Newton.
La mécanique terrestre (calcul de l'aplatissement) permet donc de distinguer deux lois d'attraction strictement équivalentes pour le mécanique céleste et donne le moyen de départager Newton et Huygens.
Les vérifications expérimentales
Les théoriciens -Newton et Huygens- affirment donc que la Terre est aplatie. Comment vérifier expérimentalement leurs propositions ? Comment déterminer la forme de la planète ? L'idée est de se servir des mesures de triangulation géodésique qui, lorsqu'elles ont réalisées à différentes latitudes, permettent de préciser la figure de la Terre.
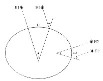
Figure 13. Détermination de la forme de la Terre par les mesures géodésiques
Les verticales sont les normales à l'ellipse et ne concourent pas au centre de la Terre. La longueur d'un arc d'ellipse de faible amplitude est sensiblement égal à celle de l'arc de cercle dont le centre est le centre de courbure de l'arc. Ainsi, pour une Terre aplatie, la longueur d'un arc de un degré est supérieure aux hautes latitudes qu'aux basses latitudes.
Les travaux de triangulation de Picard sont poursuivis en France à partir de 1683 à la fois vers le nord par J.-D. Cassini et vers le sud par La Hire (1640-1718). Vers 1701, J.-D. Cassini infère de ses observations que la longueur d'un arc de méridien de un degré est inférieure dans le nord de la France que dans le sud : la Terre serait donc allongée suivant son axe de rotation. Il reste cependant prudent. Entre 1700 et 1718, J. Cassini (1677-1756), Maraldi (1665-1729) et La Hire fils prolongent la triangulation géodésique de Dunkerque à Collioure, aux pieds des Pyrénées. À partir de leurs mesures, qui confirment la diminution de la longueur d'un degré d'arc vers le nord, J. Cassini certifie l'allongement de la Terre et s'oppose vertement aux théoriciens : la querelle sur la figure de la Terre s'envenime.
En 1720, De Mairan (1678-1771) tente de concilier la forme allongée de la Terre et l'effet indéniable d'aplatissement des forces centrifuges en affirmant que si la Terre ne tournait pas, elle serait encore davantage allongée. La solution ne satisfait personne...
Pour lever l'indécision sur la figure de la Terre et faire cesser la querelle, l'Académie décide d'envoyer, sous ordre du roi, deux missions géodésiques mesurer des arcs de méridien à des latitudes très différentes, ce qui doit faciliter les comparaisons : l'une en 1735 au Pérou (composée de Godin (1704-1760), Bouguer (1698-1758), La Condamine (1701-1774)...) et l'autre en 1736 en Laponie (composée de Maupertuis (1698-1759), Clairaut (1713-1765)...). L'expédition en Laponie, rondement menée, rapporte ses résultats dès 1737 : un degré de 57 438 toises (111,948 km) mesuré à 66° de latitude, plus grand que celui mesuré en France (57 030 toises = 111,153 km) indique clairement une Terre aplatie aux pôles (l'aplatissement trouvée est de 1/178). Les mesures de la méridienne de France, bien qu'effectuées avec soin, devaient être erronées.
La mission de Laponie ne clôt pas aussitôt les débats car les partisans de l'allongement de la Terre ne veulent pas entendre raison. Mais en 1740, Cassini de Thury (1714-1784) et La Caille (1713-1762) effectuent une nouvelle mesure de la méridienne de France et s'assurent que les degrés vont bien en augmentant vers le nord. L'expédition au Pérou, rentrée en 1744, après bien des déboires mais avec une moisson de résultats scientifiques, lève les derniers doutes avec un degré de 56 753 toises (110,613 km) mesuré à 1°30' de latitude, plus court que ceux mesurés en France et en Laponie.
Les mesures géodésiques que raille Voltaire -« Vous avez confirmé dans ces lieux pleins d'ennuis, ce que Newton connut sans sortir de chez lui »- donnent donc finalement raison aux théoriciens : la Terre est aplatie. Elles apportent une deuxième conclusion, plus fondamentale encore : l'aplatissement déterminé, voisin de 1/200, est plus proche de la valeur donnée par Newton que de celle donnée par Huygens, confirmant ainsi la conception de l'attraction universelle du premier au détriment de la conception du second. Le système de Newton sort doublement vainqueur : par rapport aux partisans de l'allongement et par rapport aux thèses de Huygens.
La Terre est-elle à l'équilibre hydrostatique ?
La polémique pourrait être close. Il n'en est rien : elle ne fait que changer de nature. Car si la Terre est bien aplatie comme le prédisait Newton, a-t-elle exactement la même figure que celle que prendrait une masse fluide ? La réponse est importante pour déterminer (le croît-on à l'époque) les conditions qui régnaient à l'origine de la Terre.
Le travail le plus remarquable sur la théorie de la figure de la Terre supposée à l'équilibre hydrostatique est effectué par Clairaut en 1743 (Figure 15). Ce dernier montre que les deux conditions d'équilibre de Newton (égalité du poids des colonnes) et de Huygens (la surface est perpendiculaire à la pesanteur) sont des conditions nécessaires mais non suffisantes et il donne une condition plus générale : « Pour qu'une masse fluide soit en équilibre et dans un état permanent, il faut que dans un canal quelconque, soit rentrant en lui-même, soit terminé de part et d'autre à la surface, les efforts des parties de fluide qu'il contient se détruisent mutuellement. »
Source - © 2001 Stetson University
Figure 15. Alexis Clairaut (1713-1765)
Clairaut découvre que l'aplatissement de la surface d'une planète en équilibre ne dépend pas seulement de la vitesse de rotation mais également de la répartition interne des densités. Si la Terre est homogène, il obtient pour l'aplatissement la valeur de Newton de 1/230. Si toute la masse est concentrée au centre, il trouve la valeur de Huygens de 1/578. Clairaut ajoute que si la Terre a été originairement fluide, les couches les plus denses sont les plus proches du centre et donc que la répartition des densités est intermédiaire entre le cas de Newton et celui de Huygens. Son aplatissement doit donc nécessairement être compris entre 1/578 et 1/230.
Ce n'est pas tout. Clairaut montre aussi que la connaissance de la valeur de la pesanteur (mesurée à l'aide de l'oscillation d'un pendule) en deux points de latitudes différentes suffit pour déterminer l'aplatissement du globe dans l'hypothèse de l'équilibre hydrostatique. C'est la naissance de la géodésie dynamique qui étudie la forme de la Terre à partir de son champ de pesanteur. Il existe donc deux méthodes indépendantes pour déterminer expérimentalement l'aplatissement du globe : les mesures géodésiques directes qui donnent l'aplatissement de la surface réelle et les mesures de la pesanteur qui donnent l'aplatissement dans l'hypothèse de l'équilibre hydrostatique.
Le "hic" est que les mesures géodésiques et de pesanteur aboutissent à des valeurs de l'aplatissement qui ne concordent pas : les premières donnent une valeur supérieure à 1/230 sortant de l'encadrement proposé par Clairaut et les deuxièmes une valeur inférieure à 1/230. Cet incompatibilité met en défaut la théorie de Clairaut et indique que la Terre ne serait pas à l'équilibre hydrostatique. D'Alembert (1717-1783) enfonce le clou : le globe étant solide, il n'y a selon lui aucune raison pour que sa figure soit semblable à celle que prendrait une masse fluide, comme le montre les grandes irrégularités de sa surface. L'incohérence des mesures géodésiques et de pesanteur n'est donc pas étonnante. Laplace (1749-1827) semble lui donner raison à la fin du siècle. En se servant de nouvelles mesures d'arcs de méridien (une dizaine) et de pesanteur (une quinzaine), il cherche à calculer l'aplatissement mais n'obtient toujours pas de valeur cohérente et conclut que la figure de la Terre n'a pas la forme régulière d'un ellipsoïde.
Source - © 1848 Académie des Sciences, Paris
Figure 16. Pierre Simon de Laplace (1749-1827)
La situation se renverse néanmoins au début du XIXe siècle. De nombreuses mesures d'arcs, en particulier celle de Maupertuis en Laponie, semblaient suspectes et ont été révisées. Les corrections apportées sont importantes et les erreurs débusquées changent radicalement la qualité des données. En 1825, Laplace trouve à partir des mesures géodésiques un aplatissement de 1/308 et à partir des mesures pendulaires un aplatissement de 1/310. Les deux aplatissements sont enfin cohérents et compris dans l'encadrement de Clairaut. Laplace peut ainsi affirmer que si la Terre devenait fluide, sa figure ne changerait pas significativement et serait très proche de celle d'un ellipsoïde.
Les explications de l'aplatissement du globe
Partisans de l'eau contre partisans du feu
Comment la Terre solide a-t-elle pu acquérir une figure d'équilibre a peu près semblable à celle que prendrait une masse fluide ? Kepler et Newton répondaient en supposant une origine fluide pour la Terre. Mais fluide par l'eau ou fluide par le feu ? La situation n'est pas claire.
À la fin du XVIIe siècle, des auteurs anglais développent des théories de la Terre où l'eau joue un rôle prépondérant. Ainsi, Burnet (1635-1715), qui a été en correspondance avec Newton, pense en 1681 que la Terre était initialement un chaos fluide de tous les éléments qui s'est mis en ordre par l'effet de la gravité : les parties lourdes descendant vers le centre, les parties légères remontant vers la surface (Figure 16). C'est grâce à la fluidité aqueuse originelle que la planète a acquis sa forme ellipsoïdale.
Clairaut s'inspire manifestement de ces théories aqueuses lorsqu'il détermine en 1743 la figure d'équilibre de la Terre en supposant qu'elle n'ait été initialement qu'un amas d'une infinité de fluides de différentes densités. Mais la fluidité qu'il invoque n'est pour lui qu'une hypothèse de calculs et son attitude dévoile l'ambiguïté des théories hydrostatiques qui supposent un équilibre fluide sans préciser ni la nature ni la cause de cette fluidité.
En 1749, Buffon (1707-1788) sort de la confusion en privilégiant une fluidité par le feu. Pour lui, la Terre et les planètes proviennent de la condensation d'un torrent de matière expulsé du Soleil à la suite d'une collision avec une comète. La Terre, constituée de matière solaire, était donc initialement en fusion, ce qui lui a permis de prendre sa forme d'équilibre ellipsoïdale. Elle s'est ensuite refroidie et consolidée tout en conservant sa forme. L'interprétation de la figure aplatie de la Terre s'ajoute donc à son hypothèse cosmogonique pour affirmer l'origine ignée du globe. La nature vitrifiée des roches et la chaleur propre de la Terre sont des indices supplémentaires pour affirmer que la Terre était en fusion au début de son histoire.
Source - © Museum of Paleontology - University of California, Berkeley
Figure 18. Buffon (1707-1788)
À la fin du XVIIIe siècle, le point de vue de Buffon est cependant oublié. C'est l'époque de la théorie neptunienne qui professe que toutes les roches, y compris le basalte et le granite, sont des produits de l'eau, formés par précipitation à partir d'un océan primordial. L'eau joue à nouveau un rôle prépondérant, en particulier pour expliquer la formation des strates sédimentaires. La figure d'équilibre de la Terre est censée mettre en évidence la fluidité aqueuse primitive de toutes les parties du globe.
La théorie neptunienne ne fait néanmoins qu'un temps et au début du XIXe siècle, elle cède devant la théorie plutoniste qui a recours à la chaleur des profondeurs pour expliquer les mouvements tectoniques et la fusion des roches volcaniques. En 1825, Laplace peut alors remettre en avant le raisonnement de Buffon : si la Terre a été initialement en fusion, les parties les plus pesantes ont pu couler vers le centre et la surface a pu prendre sa forme d'équilibre. La Terre présente bien les caractéristiques qu'on lui connaît.
Partisans du catastrophisme contre partisans de l'uniformitarisme
L'hypothèse de l'origine ignée implique que la Terre ait été au début de son histoire dans un état très différent de son état actuel. Cette idée renforce les thèses des catastrophistes qui affirment que la Terre a subit depuis son origine une évolution très marquée mais s'oppose à celles des uniformitaristes qui pensent au contraire que la Terre a toujours conservé un aspect semblable.
Les uniformitaristes cherchent ainsi à développer d'autres hypothèses pour expliquer la figure d'équilibre du globe, ne nécessitant pas d'état originel particulier. Playfair (1748-1819), J. Herschel (1792-1871) et Lyell (1794-1875) avancent dans les premières décennies du XIXe siècle que ce sont les processus d'érosion-sédimentation qui, en abrasant continuellement les reliefs et en remplissant les cavités les plus profondes, tendent à donner à la surface de la Terre solide la forme d'équilibre d'une masse fluide. Nul n'est donc besoin de supposer une quelconque fluidité, il suffit de laisser les phénomènes actuels agir pour transformer n'importe quelle planète de forme irrégulière en un ellipsoïde aplati, paraissant vérifier les lois de l'hydrostatique.
Figure 19. Charles Lyell (1797-1875)
Lamarck (1744-1829), en 1802, propose encore une autre hypothèse, prémonitoire. Il affirme que le globe possède une capacité de déformation lente qui lui permet, tout en restant solide, de s'ajuster aux forces gravitaires et centrifuges. La Terre se déformerait et s'adapterait donc continuellement à son mouvement de rotation sans avoir besoin de passer par un état fluide. Une seule condition doit être remplie : que les temps envisagés soient suffisamment importants.
Source - © UCSB/Alroy
En 1847, Spencer approfondit les remarques de Lamarck et déclare sans détour que l'aplatissement du globe ne requiert pas une fluidité originelle. Il soutient que la résistance des matériaux à la déformation décroît si leur volume augmente et qu'ainsi il suffit d'augmenter le volume d'un substance solide jusqu'à un certain point pour qu'elle cède et se comporte comme un fluide. La Terre est tellement volumineuse que les forces de cohésion deviennent négligeables devant les forces de gravité ou centrifuges et, bien que solide, elle doit avoir la même figure qu'une masse fluide.
En 1868, Reclus (1830-1905) adhère aux thèses de Spencer en notant que tous les solides sont capables de fluer et de s'adapter d'une manière permanente et irréversible lorsqu'ils sont soumis à des contraintes suffisamment fortes. La Terre qui tournoie sur elle-même depuis une infinité de temps a donc dû immanquablement s'ajuster aux forces centrifuges et ceci en dépit sa solidité. Sa figure d'équilibre n'est donc pas un gage de sa fusion initiale.
En 1876, G. Darwin (1845-1912), le fils du célèbre naturaliste, cherche à traduire ces réflexions sur la déformation de la Terre en termes mathématiques. Il affirme qu'il n'est pas impossible que la Terre ait un double comportement : à la fois élastique comme un solide pour des sollicitations brèves (vis à vis des forces de marées par exemple comme l'a montré Lord Kelvin (1824-1907) en 1862) et visqueux comme un fluide pour des sollicitations longues. Il déclare ainsi que la forme de la Terre peut revenir approximativement vers une forme d'équilibre lorsqu'elle s'en écarte trop par des ajustements et des adaptations internes. Il revient toutefois ensuite à des considérations plus sages : le globe n'a pu avoir un comportement visqueux qu'au début de son histoire lorsqu'il était proche d'un corps en fusion ; il est actuellement rigide ne pouvant assumer que des déformations élastiques de faible ampleur.
Figure 21. George Darwin (1845-1912)
Malgré les alternatives proposées, l'hypothèse de l'origine ignée pour expliquer la figure d'équilibre de la Terre continue donc d'emporter le plus de suffrages. C'est celle qui paraît la plus simple et la plus évidente.
De quelle "figure de la Terre" parle-t-on ?
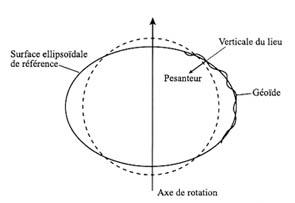
Que recouvre exactement le terme "figure de la Terre" ? La surface réelle du globe formée par les reliefs et les dépressions ? Une surface ellipsoïdale s'approchant le plus possible de la surface réelle ? Une surface en tout point perpendiculaire au champ de pesanteur telle la surface moyenne des océans ? Au cours du XIXe siècle, la nécessité d'une précision s'impose.
Playfair tente une première distinction en 1802. Il considère deux surfaces : la surface réelle, bosselée, accidentée et une surface perpendiculaire en tout point à la direction de la pesanteur. Cette dernière coïncide avec le niveau moyen des mers et « peut être supposée prolongée de la mer à travers l'intérieur des continents, jusqu'à ce qu'elle rencontre à nouveau la mer ». C'est la surface que prendrait la Terre si elle devenait parfaitement fluide. Ce n'est donc plus une surface réelle mais une surface abstraite, reliée au champ de pesanteur de la Terre (on dit que c'est une équipotentielle du champ de pesanteur car le potentiel du champ de pesanteur y garde une valeur constante).
Gauss (1777-1855) va plus loin en 1828 et distingue une surface mathématique (la surface ellipsoïdale de référence) et une surface physico-mathématique (la surface normale à la pesanteur) jusqu'alors confondues. La première a la forme régulière d'un ellipsoïde de révolution dont les paramètres (aplatissement et rayon équatorial) sont déterminés à partir des mesures d'arcs de méridien pour s'approcher au plus près de la surface réelle. Elle constitue une surface théorique de référence sur laquelle des calculs peuvent être effectués ; son étude est du ressort de la géodésie géométrique. La deuxième est la surface équipotentielle coïncidant avec le niveau moyen des océans, prolongé sous les continents. Son étude est du ressort de la géodésie dynamique. Elle est dénommée géoïde par Listing (1808-1882) en 1873.
Figure 22. Carl Friedrich Gauss (1777-1855)
La surface ellipsoïdale de référence et le géoïde ont des aplatissements semblables comme l'a montré Laplace, mais elles ne coïncident pas exactement. En effet, la Terre n'est pas homogène et les masses superficielles et les hétérogénéités de masses internes perturbent la direction de la pesanteur qui s'écarte de la normale à l'ellipsoïde. Le géoïde présente ainsi des ondulations par rapport à la surface de référence dont on cherche à connaître l'ordre de grandeur. Les travaux sur la figure de la Terre se dédoublent : déterminer le meilleur ellipsoïde de référence avant de positionner le géoïde par rapport à cette surface de référence.
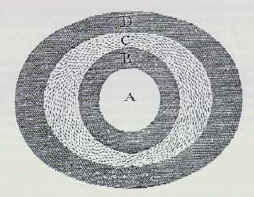
Figure 23. Le géoïde
Le géoïde, perpendiculaire à tout point à la pesanteur, s'écarte de la surface ellipsoïdale de référence à cause de la répartition irrégulière des masses internes
Stockes (1819-1903) établit en 1849 une formule permettant de calculer les écarts entre la surface de référence et le géoïde à partir de mesures de pesanteur, mais elle ne pourra être utilisée qu'à partir des années 1930-1950 lorsque des mesures intensives de pesanteur sur terre et sur mer seront réalisées pour la première fois. A son époque, on considère que les décalages entre les deux surfaces peuvent s'avérer importants et atteindre 800, voire 1000 mètres. Ils proviennent de l'attraction horizontale des continents qui "creuse" les mers en leur centre et les "relève" sur leurs bords. A la fin du XIXe siècle, on n'a pas encore saisi que l'ensemble de la surface terrestre est en équilibre isostatique et ainsi que l'attraction latérale des continents est faible.
Figure 24. George Gabriel Stockes (1819-1903)
Helmert (1843-1917), en 1901, revient sur ces conceptions. Il explique que du fait de la compensation isostatique des reliefs, les écarts entre le géoïde et l'ellipsoïde de référence restent limités et ne dépassent pas 200 à 250 mètres. Si les deux surfaces géoïdale et de référence ne coïncident pas, elles ne sont pas aussi éloignées l'une de l'autre qu'on a pu le penser à un moment donné.
Nouvelle contradiction entre théorie et mesures géodésiques
Les mesures géodésiques ont donc pour but de déterminer les paramètres de l'ellipsoïde de référence le plus adapté à la surface terrestre. Walbeck en 1819, Airy (1808-1892) en 1830, Everest (1790-1866) en 1830, Bessel (1784-1846) en 1840 proposent leur solution ; ils aboutissent tous à des aplatissements inférieurs à 1/299. Clarke (1828-1914) en 1866 puis en 1880 et Faye en 1880 reprennent à nouveau ces travaux mais arrivent cette fois respectivement à des valeurs de 1/293 et de 1/292.
Ces nouvelles valeurs de l'aplatissement posent difficultés. En effet, Poincaré (1854-1912) en 1888, à la suite de Radau en 1885, donne une nouvelle borne supérieure de l'aplatissement dans le cadre des théories hydrostatiques. Sans aucune hypothèse sur la répartition interne des densités, il montre, grâce à une astuce de calcul, que l'aplatissement doit être inférieur à 1/297, ce qui est manifestement en contradiction avec les déterminations de Clarke et de Faye. Le dilemme de Clairaut réapparaît : la Terre est-elle oui ou non à l'équilibre hydrostatique?
Figure 25. Henri Poincaré (1854-1912)
Poincaré tente une explication en supposant que la Terre, initialement en fusion, était bien à l'équilibre hydrostatique lorsqu'elle s'est consolidée. Mais que depuis ce moment la vitesse de rotation a varié, par exemple à la suite du freinage occasionné par les marées. La figure de la Terre solide ne serait donc plus aujourd'hui parfaitement ajustée à la distribution des forces centrifuges. L'incompatibilité entre les mesures géodésiques et la limite théorie de l'aplatissement serait donc un indice de la solidité du globe, qui ne posséderait pas de capacité de déformation et d'adaptation. Les considérations de Spencer et de G. Darwin sont oubliées.
Les remarques de Poincaré, bien que révélatrices d'un état d'esprit, ont une portée limitée car en 1909, Hayford (1868-1925) effectue de nouvelles mesures géodésiques et montre que les aplatissements de Clarke et de Faye étaient légèrement surestimés. Il obtient la valeur de 1/(297± 0,8), cohérente avec la limite théorique. Cette valeur est également en accord avec l'aplatissement déterminé par Helmert en 1901 à l'aide de mesures de pesanteur. Celui-ci annonce la valeur "prophétique" de 1/298,3 qui est encore retenue aujourd'hui.
Des déterminations toujours plus précises et des explications nouvelles
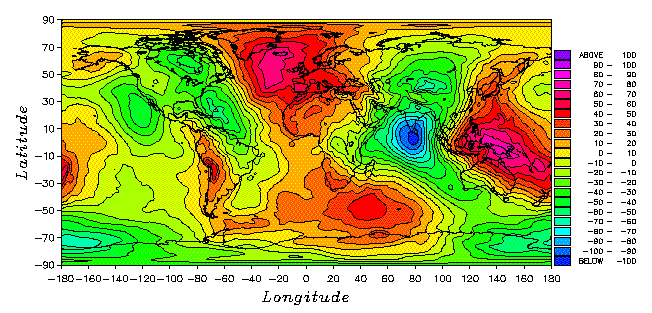
Au cours du XXe siècle, la géodésie géométrique et la géodésie dynamique vont connaître des avancés considérables, conjointement au développement générale des sciences de la Terre. Les mesures, de plus en plus nombreuses et de mieux en mieux corrigées (notamment de la compensation isostatique), permettent d'affiner toujours davantage la figure de référence et la forme du géoïde. Le lancement des satellites artificiels dans les années 1960 ouvre encore une nouvelle ère de progrès qui se poursuit actuellement. Le géoïde est déterminé aujourd'hui au-dessus des mers par altimétrie radar avec des précisions de l'ordre du centimètre, et au-dessus des continents par l'analyse des perturbations des orbites des satellites avec des précisions de l'ordre du mètre.
Le géoïde apparaît comme une surface irrégulière qui présente des ondulations par rapport à la surface ellipsoïdale de référence, avec des creux et des bosses à différentes échelles. Le creux le plus important, situé au sud de l'Inde, est de 94 m, plus faible encore que les prédictions de Helmert. Les ondulations traduisent la répartition hétérogène des masses à différentes profondeurs dans la Terre. Les irrégularités à grandes longueurs d'ondes sont attribuées aux hétérogénéités de masse du manteau profond, et les irrégularités à plus courts longueurs d'ondes reflètent les structures sous-marines liées à la tectonique des plaques.
Source - © 2001 Bureau Gravimétrique International - CNES
Figure 26. Carte du géoïde
Carte des creux (en bleu) et des bosses (en rouge) du géoïde par rapport à la surface ellipsoïdale de référence suivant le modèle franco-allemand GRIM4-C4 (Schwintzer P et al, Long-wave length global gravity field models: GRIM4-S4, GRIM4-C4, J. Geodesy, 71:189-208, 1997).
Sans entrer dans le détail des investigations, que deviennent nos deux problématiques : "comment la Terre solide peut-elle avoir une forme proche d'une forme d'équilibre ? " et "la Terre est-elle parfaitement à l'équilibre hydrostatique ?"
La rotation d'une Terre visco-élastique
À la première question, on répond encore au début du XXe siècle en invoquant la fusion originelle de la Terre. Wegener (1880-1930), en 1928, apporte cependant une autre explication. Les mouvements de compensation isostatique et d'une manière plus controversée, la dérive des continents montrent à souhait que la Terre, bien que solide pour les courtes échelles de temps, se comporte comme un fluide visqueux pour les longues échelles de temps. S'il en est ainsi, il n'y a pas de raison pour que la Terre ne se soit pas, au fil des temps, ajustée à sa rotation sans pour autant passer par un état fluide. La Terre solide se déforme pour minimiser les tensions internes et c'est pourquoi elle peut acquérir une forme d'équilibre.
Wegener pousse sa réflexion plus avant. Il remarque que si la Terre est actuellement douée d'un comportement visqueux, sa forme s'adapte à chaque perturbation de sa rotation et en particulier à un déplacement de son axe. Le renflement équatorial, qui s'ajuste continuellement à la distribution des forces centrifuges, n'occupe donc plus nécessairement une position fixe par rapport au corps de la Terre et ne peut plus assurer la stabilité de la rotation. Par sa conception des mouvements de l'axe de rotation au cours du temps, Wegener montre qu'il a saisi, bien avant la communauté géophysique, toutes les implications de la rotation d'une Terre visco-élastique.
Figure 27. Alfred Wegener (1880-1930)
Les considérations de Wegener laissent perplexes. Seul Dive les relève en 1933 et il faut attendre Gold, en 1955 pour qu'elles soient redécouvertes et pleinement acceptées. L'étude de la rotation d'une Terre visco-élastique entre alors dans sa période moderne et il ne fait plus de doute que la Terre a une forme proche d'une forme d'équilibre parce qu'elle se déforme visqueusement pour s'ajuster à sa rotation.
Figure d'équilibre et dynamique
La détermination de l'aplatissement de la surface de référence s'est continuellement précisée au cours du siècle pour arriver à la valeur actuelle de 1/298,25. Cette valeur n'est pas cohérente avec l'aplatissement de 1/299,66 calculé à partir des théories hydrostatiques.
L'explication avancée diffère cependant totalement des explications précédentes. On l'a vu, chaque écart à l'équilibre hydrostatique était interprété comme une preuve de la solidité de la Terre qui n'était pas ou plus (suite à une variation de la vitesse de rotation) ajustée aux forces centrifuges.
Aujourd'hui, les études géophysiques reconnaissent l'existence de mouvements de convection à l'intérieur du manteau terrestre, qui se traduisent par des courants chauds montants (anomalies de masse légères) et des courants froids descendants (anomalies de masse lourdes). L'intérieur du globe n'est donc pas à l'équilibre hydrostatique. Non pas parce qu'il ne peut pas s'adapter aux forces de gravité et centrifuges mais parce qu'il est animé de grands mouvements de matière générés par l'évacuation de l'énergie thermique de la Terre. Une source dynamique dérange constamment la répartition hydrostatique des densités.
La forme de la Terre est donc celle de sa figure hydrostatique légèrement perturbée par les mouvements internes de matière et l'écart entre l'aplatissement observé et l'aplatissement calculé révèle la dynamique terrestre.
Bibliographie
V. Deparis et H. Legros. Voyage à l'intérieur de la Terre. De la géographie antique à la géophysique actuelle. Une histoire des idées, Paris, CNRS Editions, 2000.
Citations
C'est à Thalès que l'on doit les premières réflexions sur la forme et la position de la Terre dans l'espace :"D'autres disent que la terre repose sur l'eau. C'est en effet la thèse la plus ancienne que nous avons reçue, et que l'on attribue à Thalès de Milet qui soutient que la terre flotte, immobile à la façon d'un morceau de bois ou de quelque autre chose de même nature (étant entendu qu'aucune ne demeure naturellement en repos sur l'air, mais au contraire sur l'eau) ; comme s'il ne fallait pas trouver une explication identique pour l'eau qui supporte la terre que pour la terre elle-même" (d'après Aristote). Retour au texte.
Anaximandre franchit une étape essentielle en osant imaginer une Terre privée de tout appui :
- "Et la Terre est suspendue, soutenue par rien, mais stable à cause de son égal éloignement de tout. Sa forme est courbée, arrondie à la façon d'une colonne de pierre ; sur l'une des faces, nous marchons, mais l'autre se trouve à l'opposé. " (d'après Hippolyte, Refutatio, I, 6, 2-7, in Anaximandre - Fragments et Témoignages, traduction de M. Conche, Paris, PUF, 1991, p. 192.)
- "[Anaximandre] affirme que la terre est, par sa forme, cylindrique, et a une profondeur qui est le tiers de sa largeur." (d'après Pseudo-Plutarque, in Anaximandre - Fragments et Témoignages, traduction de M. Conche, Paris, PUF, 1991, p. 193.)
- "Certains disent que la terre demeure en repos par indifférence : ainsi Anaximandre, parmi les Anciens. Car se mouvoir vers le haut, vers le bas ou vers les côtés, l'un pas plus que l'autre ne convient à ce qui est établi au centre et se comporte pareillement à l'égard de tous les points extrêmes ; et comme il lui est impossible d'effectuer en même temps un mouvement dans des directions contraires, il s'ensuit que la terre doit nécessairement rester au repos." (Aristote, Du Ciel, II, 13, 295b, 11-16 ; in Anaximandre - Fragments et Témoignages, traduction de M. Conche, Paris, PUF, 1991, p. 194.)
Platon ne suppose encore la forme sphérique de la Terre qu'à titre d'hypothèse : "Ma conviction à moi [c'est Socrate qui parle], c'est, en premier lieu, que si la terre est au centre du monde et avec la forme d'une sphère, elle n'a besoin, pour ne pas tomber, ni de l'air, ni d'aucune autre semblable résistance ; mais il y a assez pour la maintenir, de la similitude, en tous sens, du monde avec lui-même et de la façon dont se contrebalancent tous les points de la terre, car pour une chose qui se contrebalance de la sorte, il n'y aura, du moment qu'elle a été placée au centre de quelque chose qui possède avec soi-même une égale similitude, aucune raison pour qu'elle penche plus ou moins d'aucun côté demeurera immobile." (in Platon, Apologie de Socrate, Criton, Phédon, Paris, Gallimard, 1950, p. 207.) Retour au texte.
La Terre a des dimensions précises qui peuvent se calculer. Aristote avance une première valeur, sans doute due à Eudoxe : "Et parmi les mathématiciens, ceux qui essayent de calculer la grandeur de la circonférence terrestre arrivent à une mesure d'environ 400 000 stades [soit près de 74 000 km]. Il résulte de ces preuves non seulement que la terre est nécessairement de forme sphérique mais encore qu'elle n'est pas d'une grandeur considérable comparée à la grandeur des autres astres." (Aristote, Du Ciel, II, 14, 298a, 20, Paris, J. Vrin, 1949, p. 117.) Retour au texte.
Du temps de Jean Buridan, au XIVe siècle, les trois quarts de la surface terrestre restent inexplorés : "Toutes les mers que quelque homme a pu traverser et toutes les terres habitables qui ont pu être découvertes sont contenues dans le quartier que nous habitons ; certains se sont efforcés de traverser la mer pour parvenir à d'autres quartiers ; jamais ils n'ont pu parvenir à quelque terre habitable ; aussi dit-on qu'Hercule, aux confins du quartier que nous habitons, a placé des colonnes pour signifier qu'au-delà, il n'y a plus terre habitable ni mer qu'on puisse traverser." (J. Buridan , In P. Duhem, Le Système du Monde, tome IX, Paris, Hermann, 1958, p. 196.) Retour au texte.
Jean Buridan pense que la terre et l'eau forment deux sphères décalées l'une par rapport à l'autre :
- "Première conclusion. Toutes choses égales d'ailleurs, et sous le même volume, la terre que l'eau recouvre est plus grave que la terre découverte ; le Soleil, en effet, échauffe davantage la terre découverte ; comme nous l'avons dit précédemment, celle-ci devient plus poreuse, elle participe davantage de l'air qui se trouve dans ses pores ou qui lui est mêlé, et aussi des gaz."
- "Seconde conclusion. Le centre de gravité de la terre n'est pas le même point que le centre de grandeur. Nous parlons ici de la masse totale de la terre."
- "Troisième conclusion. De là il résulte que le volume terrestre n'est pas concentrique mais excentrique au Monde. On nomme en effet concentrique au Monde ce dont le centre coïncide avec le centre du Monde ; c'est le centre de gravité de la terre qui est le centre du Monde, car c'est en raison de sa pesanteur, et non de sa grandeur, que la terre occupe le lieu central ; c'est en vertu de sa pesanteur qu'elle s'équilibre au centre du Monde comme deux poids égaux se font, l'un à l'autre, équilibre dans une balance, bien que leurs volumes soient inégaux."
- "Quatrième conclusion. Lors même que la terre tout entière serait rendue parfaitement sphérique, comme il arriverait si, demain, Dieu prenait les montagnes pour combler les vallées, la partie que la mer recouvre aujourd'hui n'en continuerait pas moins d'être recouverte, et la partie qui est découverte resterait découverte. […] En voici la cause : l'eau coule toujours au plus bas lieu, c'est-à-dire au lieu le plus rapproché du centre du Monde ; or la surface de l'hémisphère le plus pesant se trouverait ainsi plus bas placé et la surface de l'hémisphère le plus léger serait plus haut ; la mer, donc, délaisserait la partie la plus élevée pour couler vers la plus basse. De là suit ce corollaire : il n'est pas nécessaire d'imaginer que les océans résident dans une vallée ou une partie concave de la surface terrestre ; ils recouvrent la partie la plus basse de cette surface, et ils la recouvriraient encore, si la terre entière était parfaitement sphérique et ne présentait aucune partie concave. Mais touchant les mers partielles, force est de considérer qu'elles se trouvent dans des vallées ou des parties concaves de la terre ; au-dessous d'elles la terre est déprimée par rapport à sa sphéricité."
(J. Buridan , In P. Duhem, Le Système du Monde, tome IX, Paris, Hermann, 1958, p. 199-200.) Retour au texte.
Les voyages de découverte prouvent que la terre et l'eau sont imbriquées l'une dans l'autre pour ne constituer qu'une seule et même sphère, comme le rapporte Nicolas Copernic : "La terre également est sphérique puisqu'elle s'appuie sur son centre par toute partie. […] Comment la terre avec l'eau effectue un globe. Donc l'Océan répandu autour de celui-ci, répandant lui-même de tous côtés les mers, emplit ses descentes plus inclinées. Et ainsi il fallait qu'il y ait moins d'eau que de terre, afin que l'eau n'absorbât pas toute la terre, les deux tendant avec effort vers le même centre part leur gravité, mais de sorte qu'elle laissât certaines parties de la terre pour le bien-être des êtres animés et tant d'îles à découvert d'un côté de l'autre. […] Bien sûr il est nécessaire que la terre ait avec ce qui coule autour, une telle figure, telle que montre son ombre : en effet elle fait la Lune manquante selon les circonférences du cercle délivré. La terre n'est donc pas plane […] mais délivrée selon la rondeur comme les philosophes pensent." (N. Copernic, Des révolutions, 1543 ; trad. de J. Peyroux, Paris, Blanchard, 1987, p.17-19.) Retour au texte.
Kepler apporte plusieurs éléments sur la sphéricité de la Terre.
- L'examen de la répartition des mers et de la hauteur des continents, partout sensiblement la même, permet à Kepler d'affirmer que la terre solide a la même figure d'équilibre que la mer : "Examine attentivement que les Mers, de la façon dont elles se réunissent immédiatement entre soi, les Isthmes se plaçant entre, l'expérience étant témoin, obtiennent presque la même hauteur et ainsi tous les littoraux tout à l'entour. Ensuite considère avec soin les origines des Fleuves qui se déchargent dans cette Mer, presque toujours dans les plus hautes montagnes des plus profonds Continents. Presque toujours encore les sources de beaucoup de fleuves coulant vers les diverses régions sont très proches entre soi, une chaîne modérée se trouvant entre les montagnes. C'est pourquoi nulle partie de la Terre n'est beaucoup plus haute que les plus hautes sources des fleuves. Si donc les sources ne sont pas beaucoup plus hautes que les littoraux, les sommets également des montagnes les plus hautes ne s'élèvent pas beaucoup au-dessus de la même hauteur des littoraux et pour cette raison de la hauteur de la mer entourant de partout." (J. Kepler, Abrégé d'astronomie copernicienne, 1618 ; trad. de J. Peyroux, Paris, Blanchard, 1988, p.41-42.)
- Kepler avance un argument géodésique pour la sphéricité du globe : "Chaque fois que nous avançons ou sur terre ou sur mer par des chemins d'espaces égaux, en ligne droite vers le Nord, nous saisissons autant de fois en Astronomie des accroissements ou des diminutions égaux des hauteurs du soleil et des étoiles sur le méridien : chaque fois que nous nous transportons sur un même parallèle par des intervalles égaux de chemin vers le Levant ou le Couchant, autant de fois nous comptons également davantage ou un peu moins d'heures et de minutes dans les commencements ou les fins des Eclipses lunaires ; mais si la Terre n'était pas ronde, il n'y aurait pas cette égale proportion des lieux. Donc la Terre est ronde tant vers le Nord et le Sud que vers le Levant et le Couchant." (J. Kepler, Abrégé d'astronomie copernicienne, 1618 ; trad. de J. Peyroux, Paris, Blanchard, 1988, p.45.)
- Selon Kepler, le fait que la Terre solide soit sphérique impose qu'elle ait été dans un état de fluidité (par le feu ou par l'eau) au début de son histoire : "Toutes les parties de l'eau ne pourront établir une autre figure du tout que la ronde parce que la force d'unir dans les eaux non empêchée, ni par soi, ni par la terre, fait principalement une unique figure ; elle est ronde de ce mode, n'ayant rien en dehors de soi. D'où n'est faite aucune saillie de l'eau au-dessus de la rondeur, aucun flot de l'Océan ne demeure longtemps suspendu et en monceau. […] Est-ce que par hasard les mêmes choses ne pourraient pas être dites au sujet de la Nature de la Terre ? Certes la terre, lorsqu'elle fut créée par Dieu, ou fut elle-même une certaine masse fluide et molle, et devint dure, et alors les mêmes choses qui ont été dites au sujet de l'eau sont encore vraies au sujet de la terre ; ou elle fut créée dans sa solidité ou dureté particulière, et alors il n'est certes pas ainsi vraisemblable qu'une autre figure lui ait été introduite si elle avait été molle au début. En effet bien qu'elle soit dure, pourtant le corps est soit de matière comme l'Eau et de liquide macéré, ou liquéfié par le feu elle peut être faite fluide comme l'eau par parties. Il convient donc qu'elle ait encore reçu la propre figure de la matière fluide, ce qui est ronde. Pourquoi donc la terre n'est pas parfaitement ronde comme est l'Océan ? Le très sage fondateur distribua parmi la nature la Matière, et parmi l'usage des Etres animés, à cause duquel encore la Terre a été faite dure, sa figure par une proportion très délibérée, de sorte que les montagnes fussent certes un jour élevées, et que les vallées fussent abaissées pour recevoir les eaux répandues perpétuellement ; assurément pour le sens, quand toute la Sphère vient à la fois dans la vue avec ses éminences, rien ne semblerait s'éloigner de la parfaite rondeur." (J. Kepler, Abrégé d'astronomie copernicienne, 1618 ; trad. de J. Peyroux, Paris, Blanchard, 1988, p.42-43.)
En 1686-1687, Hooke affirme que du fait de la rotation terrestre, les océans ont une figure ellipsoïdale : "Je suppose que la forme de la surface des eaux est, et a été, depuis le début de l'histoire de la Terre, une forme ovale, dont les plus longs diamètres se situent dans le plan de l'équateur, et dont le plus court est l'axe même de la rotation." (R. Hooke, A Discourse of Earthquake, 1687 ; réédité in The Posthumous Works of Robert Hooke, The Source of Science, n°73, New York et Londres, Johnson, 1969, p.346). Il comprend que la gravité est composée de deux forces agissant dans des directions différentes : l'attraction dirigée vers le centre de la Terre et la force centrifuge dirigée perpendiculairement à l'axe de rotation : "Si la capacité de gravitation de la Terre est partout égale, […] alors cette capacité doit être composée avec une tendance contraire des corps lourds à s'écarter de leur axe de rotation. Si cela est supposé, une partie de la gravité vers le centre de tels corps doit être enlevée par ce Conatus, qui est partout oblique, sauf sous l'équateur, où la gravitation est le plus fortement diminuée. Par conséquent, la gravité doit agir le plus librement et le plus puissamment sous les pôles." (R. Hooke, A Discourse of Earthquake, 1687 ; réédité in The Posthumous Works of Robert Hooke, The Source of Science, n°73, New York et Londres, Johnson, 1969, p.349). Retour au texte.
En 1687, Newton suppose que la Terre solide a une figure ellipsoïdale du fait de sa rotation : "Si les planètes n'avaient point le mouvement journalier de rotation autour de leur axe, elles devraient être sphériques à cause de l'égale gravité de leurs parties. Le mouvement de rotation fait que les parties qui s'éloignent de l'axe font effort pour monter vers l'équateur. Et, par conséquent, si la matière dont elles sont composées était fluide, son élévation vers l'équateur augmenterait le diamètre de ce cercle, et son abaissement vers les Pôles diminuerait l'axe. Aussi les observations astronomiques nous apprennent-elles que dans Jupiter le diamètre qui va d'un pôle à l'autre est plus court que celui qui va de l'Orient à l'Occident. Par le même raisonnement, on verra que si notre terre n'était pas un peu plus haute à l'équateur qu'aux pôles, les mers s'affaissant vers les pôles, et s'élevant vers l'équateur, inonderaient toutes ces régions." (I. Newton, Principes mathématiques de la philosophie naturelle, 1687 ; trad. de la marquise de Chastelet, 1756, rééd. Paris, A. Blanchard, 1966, livre III, proposition 18, p. 34.). Retour au texte.
En 1690, Huygens expose que la surface de la Terre est en équilibre si elle est en tout point perpendiculaire à la verticale :"La Terre n'est pas tout à fait spherique, mais d'une figure de sphere abaissée vers les deux Poles, telle que seroit à peu près une Ellipse, en tournant sur son petit axe. Cela procede du mouvement journalier de la Terre, et c'est une suite nécessaire de la declinaison susdite du plomb. Parce que la descente des corps pesans estant parallele à la ligne de cette suspension, il faut que la surface de tout liquide se dispose en sorte, que cette ligne luy soit perpendiculaire, parce qu'autrement il pourroit descendre d'avantage. Partant la surface de la mer est telle, qu'en tout lieu le fil suspendu luy est perpendiculaire. D'ou s'ensuit que la ligne du niveau, c'est-à-dire celle qui coupe le fil, du plomb suspendu, à angles droits, doit marquer l'horizon, ainsi qu'elle fait ; n'y ayant que la hauteur du lieu, ou le niveau est placé, qui le fasse viser quelque peu plus haut. Or les costes des terres estant generalement elevées, et presque par tout de mesme, à l'égard de la mer ; il s'ensuit que tout le composé, de terres et de mers, est reduit à la mesme figure spheroïde que la surface de la mer se donne necessairement. Et il est à croire, que la Terre a pris cette figure, lors qu'elle a esté assemblé par l'effet de la pesanteur : sa matiere ayant dés lors le mouvement circulaire de 24 heures." (CH. Huygens, Discours de la cause de la pesanteur, in Triaté de la lumière, 1690 ; rééd. Londres, Dawsons of Fall Mail, 1966, p.152.). Retour au texte.
La mesure de l'arc de méridien en Laponie ne met pas fin à la controverse sur la figure de la Terre : "Les partisans de l'allongement de la Terre firent d'abord toutes les objections qu'il était possible d'imaginer contre les opérations sur lesquelles était appuyée la mesure du nord. On crut, dit un auteur moderne, qu'il y allait de l'honneur de la Nation à ne pas laisser donner à la Terre une forme étrangère, une figure imaginée par un Anglais ou un Hollandais, à peu près comme on a cru longtemps l'honneur de la Nation intéressé à défendre les tourbillons et la matière subtile [de Descartes] et à proscrire la gravitation newtonienne. Paris et l'Académie se divisèrent entre les deux partis. Enfin, la mesure du Nord fut victorieuse et ses adversaires furent si convaincus qu'ils demandèrent qu'on mesurât une seconde fois les degrés du méridien dans toute l'étendue de la France. L'opération fut faite plus exactement que la première fois, l'astronomie s'étant perfectionnée beaucoup dans l'intervalle des deux mesures : on s'assura en 1740 que les degrés allaient en augmentant vers le nord et, par conséquent, la Terre se retrouve aplatie. C'est ce qu'on peut voir dans le livre qui a pour titre La Méridienne de France, vérifiée dans toute l'étendue du royaume par M. Cassini de Thury (1744)" (J. D'Alembert, "Figure de la Terre", Encyclopédie ou Dictionnaire raisonné des sciences..., Paris, Briasson, David, Le Breton, Durand puis Neuchâtel, Faulche, 1751-1765.). Retour au texte.
Clairaut donne plusieurs indices pour défendre l'hypothèse selon laquelle la Terre se trouve à l'équilibre hydrostatique : "Quand on considère tout ce qui compose la surface de notre globe, les continens, les mers, les lacs, les montagnes, les courans des fleuves, etc. ; on est d'abord porté à croire que toutes les recherches que peut fournir la théorie pour déterminer la figure de la terre, sont de vaines spéculations, et que même la mesure actuelle, ne saurait nous en faire connaître que de très petites parties, sans en pouvoir conclure pour le tout. Quand on remarque ensuite que les mers communiquent ensemble de toutes parts, que les côtes ne sont que très-peu élevées au-dessus de la mer, que la hauteur des plus grandes montagnes est presque nulle en comparaison du diamètre de la terre, que la déclivité des plus grands fleuves ne suppose pas que leurs sources soient plus élevées au-dessus du niveau de la mer, que ne le sont les montagnes ; on vient bientôt à reconnaître que la figure de la terre doit dépendre des lois de l'hydrostatique, et que les opérations faites pour la mesurer doivent donner à peu près les mêmes résultats que si on les faisait sur une masse d'eau qui se serait durcie après avoir pris la figure que demande l'équilibre." (A. Clairaut, Théorie de la figure de la Terre, tirée des principes de l'hydrostatique, 1743 ; 2nde éd. Paris, Courcier, 1808, p. vii.). Retour au texte.
Clairaut énonce clairement que la pertinence de sa théorie de l'équilibre hydrostatique de la Terre dépend de la valeur trouvée pour l'aplatissement : "Ce rapport [l'aplatissement] une fois déterminé, s'il se trouve plus petit que celui de 230 à 231, il sera facile, par ce qui précède, de former des hypothèses sur l'intérieur de la Terre qui conviennent avec la théorie et les observations, soit qu'on admette que la Terre ait été originairement fluide, soit qu'on ne l'admette pas. Mais si ce rapport se trouvait incontestablement plus grand que celui de 230 à 231, j'avoue que, non seulement il faudrait abandonner la théorie que j'ai établie […], mais qu'il serait difficile de concilier les mesures du pendule avec celles des degrés dans le système de M. Newton. Je crois même pouvoir assurer que si l'on y réussissait, ce ne pourrait être qu'en employant des hypothèses qui auraient bien peu de vraisemblance." (A. Clairaut, Théorie de la figure de la Terre, tirée des principes de l'hydrostatique, 1743 ; 2nde éd. Paris, Courcier, 1808, p. 301-302.). Retour au texte.
Pour D'Alembert, la Terre est bosselée et n'a pas la même figure qu'une masse fluide : "M. de Buffon est le premier (que je sache) qui ait avancé que la Terre a vraisemblablement de grandes irrégularités dans sa figure. […] Si la Terre avait été particulièrement fluide et homogène, la gravitation mutuelle de ses parties, combinée avec la rotation autour de son axe, lui eût certainement donné la forme d'un sphéroïde aplati, dont tous les méridiens eussent été semblables : si la Terre eût été originairement formée de fluides de différentes densités, ces fluides, cherchant à se mettre en équilibre entre eux, se seraient aussi disposés de la même manière dans chacun des plans qui auraient passé par l'axe de rotation du sphéroïde, et par conséquent les méridiens eussent encore été semblables. Mais est-il bien prouvé, dira-t-on, que la Terre ait été originairement fluide ? Et, quand elle l'eût été, quand elle eût pris la figure que cette hypothèse demandait, est-il bien certain qu'elle l'eût conservée ? Pour ne pas dissimuler ni diminuer la force de cette objection, appuyons-la encore, avant que d'en apprécier la valeur, par la réflexion suivante. La fluidité du sphéroïde demande une certaine régularité dans la disposition de ses parties, régularité que nous n'observons pas dans la Terre que nous habitons. La surface du sphéroïde fluide devrait être homogène ; celle de la Terre est composée de parties fluides et de parties solides, différentes par leur densité. Les bouleversements évidents que la surface de la Terre a essuyés, bouleversements qui ne sont cachés qu'à ceux qui ne veulent pas les voir (et dont nous avons qu'une faible, mais triste image, dans celui que viennent d'éprouver Quito, le Portugal et l'Afrique) [allusion à des tremblements de terre], le changement évident des terres en mers et des mers en terres, l'affaissement du globe en certains lieux, son exhaussement en d'autres, tout cela n'a-t-il pas dû altérer considérablement la figure primitive ? […] Or la figure primitive de la Terre étant une fois altérée, et la plus grande partie de la Terre étant solide, qui nous assurera qu'elle ait conservé aucune régularité dans sa figure ni dans la distribution de ses parties ? Il serait d'autant plus difficile de la croire, que cette distribution semble, pour ainsi dire, faite au hasard dans la partie que nous pouvons connaître de l'intérieur et de la surface de la Terre." (J. D'Alembert, "Figure de la Terre", Encyclopédie ou Dictionnaire raisonné des sciences..., Paris, Briasson, David, Le Breton, Durand puis Neuchâtel, Faulche, 1751-1765.) Retour au texte.
Buffon affirme que la Terre est issue du Soleil et qu'elle était au début de son histoire dans un état de liquéfaction totale :"La Terre et les Planètes, au sortir du Soleil, étoient donc brûlantes et dans un état de liquéfaction totale. Cet état de liquéfaction n'a duré qu'autant que la violence de la chaleur qui l'avoit produit ; peu à peu les planètes se sont refroidies, et c'est dans le temps de cet état de fluidité causée par le feu qu'elles auront pris leur figure, et que le mouvement de rotation aura fait élever les parties de l'équateur en abaissant les pôles." (Buffon, Théorie de la Terre ; in Oeuvres philosophiques, Paris, PUF, 1954, p. 72.). Retour au texte.
Laplace explique la figure d'équilibre de la Terre par son origine ignée. Il s'interroge "sur la cause qui a donné aux couches du sphéroïde des formes a peu près elliptiques et de densité croissante de la surface au centre, qui les a disposées régulièrement autour de leur centre commun de gravité et qui a rendu sa surface très peu différente de celle qu'elle eût prise si elle avait été primitivement fluide. […] Si les diverses substances qui composent la Terre ont eu primitivement, par l'effet d'une grande chaleur, l'état fluide, les plus denses ont dû se porter vers le centre ; toutes ont pris des formes elliptiques, et la surface a été en équilibre. En se consolidant, ces couches n'ont changé que très peu de figure, et alors la Terre doit offrir présentement les phénomènes dont je viens de parler. Ce cas a été amplement discuté par les géomètres." (P. S. Laplace, Traité de mécanique céleste, tome V, 1825, rééd. américaine, New York, Alk. Paper, 1969, p. 20-21.). Retour au texte.
Playfair pense que ce sont les phénomènes d'érosion-sédimentation qui ont permis à la Terre d'acquérir sa figure d'équilibre : "Cependant, si nous supposons que les parties solides de cette masse peuvent être dissoutes ou abrasées, et emportées vers l'océan, il existe une tendance pour que le corps prenne dans son ensemble la même figure que s'il avait été entièrement fluide, et sujet aux lois de l'hydrostatique." (Playfair, Illustrations of the Huttonian Theory of the Earth, Edinburgh, W. Creech, 1802, rééd. New York, Dover Publications, 1964, p. 497-498.). Retour au texte.
Herschel soutient l'opinion de Playfair : "Comme masse solide, elle [la Terre] peut résister à des forces auxquelles l'eau obéit librement ; mais lorsque, dans son état de dégradation subite ou successive, elle se trouve disséminée dans l'eau, sous forme de sable ou de limon, elle participe à tous les mouvements de ce liquide. Ainsi, dans le cours des siècles, les continents seront détruits, et leurs débris se répandront sur le fond de l'océan, où, remplissant les cavités les plus profondes, ils tendront continuellement à rendre à la surface du noyau solide la forme d'équilibre." (J. Herschel, in C. Lyell, Principles of Geologie, 4e éd., 1840, trad. française, Paris, Langlois et Leclercq, 1843, p. 476-477.). Retour au texte.
Lamarck propose une adaptation continuelle du globe aux forces centrifuges, suite à un lent basculement de l'axe de rotation : "Par suite de plusieurs genres d'observations [les fossiles en haut des montagnes], j'ai parlé du déplacement des points polaires, et j'ai cité le rapprochement réel de celui qu'on nomme boréal de l'Europe que nous habitons. La plus grande vraisemblance m'indique qu'une révolution complète des points polaires doit suivre entièrement la révolution du déplacement du bassin des mers, et conséquemment s'exécuter avec une lenteur tout aussi considérable, c'est-à-dire, exiger des millions de siècle pour s'opérer. Dans cet état de choses, je pense que le déplacement des aplatissements polaires et des élévations équatoriales, non seulement suivra le déplacement des deux points de rotation du globe, mais que le changement qu'il entraînera dans la forme externe de ce globe pourra véritablement s'effectuer sans qu'il soit nécessaire que les matières qui forment la masse générale du globe soient liquides. On a jugé cette condition (la liquidité) nécessaire, parce que l'on a supposé que la forme sphéroïde du globe terrestre avait été acquise dans un espace de temps fort court. Mais comme il y a lieu de croire que cette forme n'a eu lieu qu'à l'aide d'un tems dont la longueur est presqu'incalculable, les déplacemens des parties protubérantes et des côtés déprimés peuvent aussi, à l'aide de beaucoup de tems, s'opérer avec ceux de la direction de la cause qui occasionne ces dépressions et ces protubérances. Cela est d'autant plus possible, qu'il est évident pour moi que le globe terrestre n'est point du tout un corps entièrement et vraiment solide, mais que c'est une réunion de corps plus ou moins solides, déplaçables dans leur masse ou dans leurs parties, et parmi lesquels il s'en trouve un grand nombre qui subissent des changemens continuels dans leur état." (J.-B. Lamarck, Hydrogéologie, Paris, Agasse et Maillard, 1802, p. 178-179; trad. américaine, Urbana, University of Illinois Press, 1964, p. 130-131.). Retour au texte.
Spencer affirme que l'aplatissement du globe n'implique pas une fluidité originelle : "L'on admet généralement que la forme sphéroïdale de la Terre -qui indique l'obéissance à la force centrifuge- implique un état premier de fluidité. Si toutefois on peut montrer qu'en dépit de sa solidité apparente, la Terre doit à l'instant présent être entièrement soumise aux influences affectant sa configuration générale et qu'elle est encore plastique pour ce qui est des forces centrifuges et de la gravitation, la théorie de la fluidité initiale, aussi probable soit-elle pour d'autres raisons, ne peut plus se déduire à partir de l'aplatissement de la Terre aux pôles. [...] Ces faits et des faits semblables innombrables indiquent que la fluidité et la solidité sont dans une grande mesure des qualités de degré ; que la tenacité cohésive qu'un morceau de matière oppose aux forces naturelles tendant à fracturer cette matière décroît avec constance lorsque la masse de la matière augmente ; ainsi donc, pour toute substance, aussi solide paraisse-t-elle à nos perceptions, il suffit d'augmenter son volume jusqu'à un certain point pour qu'elle cède et devienne dans un sens fluide devant les forces de la gravitation et autres. [...] Le fait que la Terre soit un sphéroïde aplati ne paraît pas apporter un quelconque soutien à l'hypothèse de la fluidité originelle, comme cela est compris habituellement." (H. Spencer, "The Form of the Earth no proof of Original Fluidity", Philosophical Magasine, 3, 20, 194-196, 1847.). Retour au texte.
Reclus appuie le raisonnement de Spencer : "L'aplatissement de la Terre aux deux pôles et le renflement équatorial ont été présentés comme des témoignages irrécusables de l'état d'incandescence liquide dans lequel se serait autrefois trouvé le globe. [...] Mais on peut se demander si un globe, même solide, ne se renflerait pas aussi vers l'équateur, en tournoyant sans repos pendant une série indéfinie de siècles, car il n'est pas une matière qui soit absolument inflexible, et sous les fortes pressions de nos laboratoires, bien inférieures certainement aux pressions des forces planétaires, tous les corps solides, comme le fer et l'acier, s'écoulent à la façon des liquides." (E. Reclus, La Terre - Description des phénomènes de la vie du globe, Paris, Hachette, 1868, p. 26-27.). Retour au texte.
Listing différencie le géoïde, qui correspond au niveau moyen des mers prolongé sous les continents, de la surface ellipsoïdale de référence : "Nos interrogations impliquent deux surfaces mathématiques, toutes deux de forme ellipsoïdale, l'une selon une approche plutôt physique, l'autre dans une acceptation mathématique abstraite. Nous appellerons la première, qui est partiellement formée par la surface des océans, la surface géoïdale de la Terre ou le géoïde, alors que nous conserverons le terme sphéroïde pour la seconde, laquelle, représentée par une formule mathématique simple, suit au plus près la forme et les dimensions du géoïde. Ces termes doivent raisonnablement éviter la confusion rendue presque inévitable par l'expression surface mathématique appliquée tout aussi souvent à la seconde qu'à la première surface." (J. B. Listing, "Über unsere jetzige Kenntniss der Gestalt und Grösse der Erde", Königliche Gesellschaft der Wissenschaften, 33-98, 1873.). Retour au texte.
Poincaré cherche à expliquer l'écart entre l'aplatissement théorique et l'aplatissement déterminé par les mesures géodésiques : "Une explication serait que l'hypothèse de Clairaut n'est approchée qu'aux termes du second ordre près. M. Callandreau, qui a fait le calcul, a montré que considérer les termes du second ordre reviendrait à creuser l'ellipsoïde de 9 mètres seulement. C'est négligeable. On pourrait alors se demander jusqu'à quel point l'hypothèse de Clairaut serait exacte : par exemple, on peut supposer la terre complètement solide sauf la mer. Au moment de la solification, les couches obéissaient à la loi de Clairaut mais, depuis ce moment, la vitesse de rotation aura pu varier (par exemple, les marées diminuant cette vitesse de rotation) ; et de plus l'aplatissement des ellipsoïdes internes aura pu se modifier par suite des tassements qui ont produit les continents et les montagnes. Enfin on pourrait supposer qu'une portion intérieure de la terre est restée fluide : les deux parties fluide et solide, agiraient alors séparément dans le phénomène de la précession : mais l'hypothèse de la fluidité intérieure de la terre n'est guère vraisemblable." (H. Poincaré, Figure d'équilibre d'une masse fluide, Paris, Naud, 1902, p. 96.). Retour au texte.
Wegener explique comment les déformations visqueuses de la Terre permettent des grands déplacements de l'axe de rotation : "L'apparition des mouvements compensateurs isostatiques, ainsi que les translations continentales, montrent à souhait que la terre possède un certain degré de fluidité et, s'il en est ainsi, on ne voit pas pourquoi le renflement équatorial ne pourrait pas changer de position. […] Supposons que le pôle d'inertie subisse un petit écart x (sans que le renflement équatorial subisse de variation) à cause de phénomènes géologiques. Le pôle de rotation le suivra nécessairement dans son mouvement. La rotation de la terre s'effectuera donc autour d'un nouvel axe, s'écartant un peu de l'ancien. Ce mouvement entraînera un déplacement du renflement équatorial. A cause de la viscosité du noyau de la terre cette adaptation n'a lieu que très lentement, il est même possible qu'elle ne s'accomplisse pas toujours et qu'elle subisse un arrêt ; sur ces circonstances nous ne savons rien. Comme première approximation, nous serons obligés d'admettre qu'une adaptation complète a lieu, fût-ce après une longue durée. Une fois cet état atteint, nous nous retrouvons dans les conditions initiales ; la cause d'origine géologique intervient de nouveau, le pôle subira un nouvel écart x, dans le même sens, et le phénomène pourra se reproduire un nombre quelconque de fois. Au lieu du déplacement initial d'écart x, nous avons à faire à un déplacement progressif, dont la vitesse dépend de l'écart initial x et de la viscosité de la terre et qui ne cesse qu'après disparition de l'effet dû à la cause d'origine géologique ; si cette masse consistait par exemple, en l'addition d'une masse m, quelque part dans les latitudes moyennes, le déplacement axial ne cessera que lorsque cette masse additionnelle arrivera à l'équateur ou, pour nous exprimer d'une façon plus propre, lorsque l'équateur l'aura atteinte." (A. Wegener, La genèse des continents et des océans, 1928 ; rééd. Paris, C. Bourgois, 1990, p.152-153.) Retour au texte.