Article | 01/10/2014
La force de marée
01/10/2014
Résumé
Référentiel galiléen ou géocentrique, bien se repérer pour "ressentir" et définir la force de marée.
Table des matières
Repères et forces en présence
Pour simplifier nous allons considérer deux astres seulement : un astre attirant, la Lune, un astre attiré, la Terre. Ce sont donc les effets de la force de marée lunaire sur la Terre que nous allons examiner (l'inverse existe aussi et nous donnerons ses conséquences dans un futur chapitre).
Expliquer la force à l'origine des marées n'est pas simple car pour bien faire cela requiert quelques notions de mécanique, notamment que la loi est vraie uniquement dans les référentiels appelés galiléens[1].
Il faut savoir que si la Lune tourne autour de la Terre, la Terre tourne autour de la Lune. Tout dépend bien sûr du référentiel dans lequel on se place. Deux référentiels sont utiles : celui qui est centré au centre de masse du système Terre-Lune (et donc à environ 5000 km du centre de la Terre) et dont les axes sont de directions fixes. Celui-ci est galiléen (toujours en supposant que le système Terre-Lune est isolé), nous le noterons 𝓡. Dans ce référentiel les centres de la Terre et de la Lune tournent autour du centre Terre-Lune en gardant ces trois points alignés. Le deuxième référentiel est centré au centre de la Terre et ses axes sont de directions fixes : dans celui-ci le centre de la Terre est immobile mais il faut ajouter des forces d'inertie aux vraies forces. C'est dans ce deuxième référentiel que les forces de marées sont ressenties, nous l'appellerons référentiel géocentrique et le noterons 𝓡g.
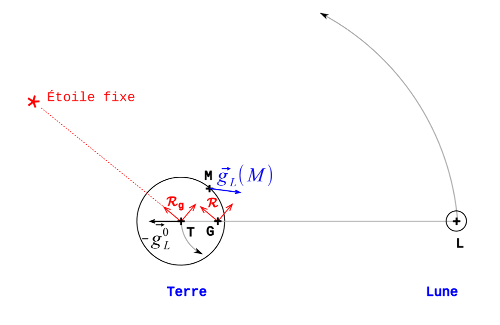
Figure 1. Schéma du système Terre-Lune
La Terre, de centre T, et la Lune, de centre L, tournent toutes deux, à la manière d'une haltère, autour de leur centre de masse commun, G, situé à environ 1000 km de profondeur dans la Terre. Les référentiels, en rouge, sont choisis de telle façon que leurs axes pointent vers des étoiles "fixes (plus exactement des objets célestes les plus fixes possibles comme les quasars). Le référentiel 𝓡 centré en G est galiléen alors que le référentiel géocentrique 𝓡g ne l'est pas. Dans ce dernier référentiel tout point M subit l'attraction lunaire mais aussi une force inertielle apparente .
D'autre part il est important de bien réaliser que l'attraction de la Lune peut être décomposée en deux termes :
- la moyenne de l'attraction lunaire sur la Terre[2] est la source du mouvement orbital de la Terre (elle tourne autour du centre de masse Terre-Lune) ; ce terme intéresse les mécaniciens célestes.
- les écarts à la moyenne (l'attraction varie dans l'espace en intensité et en direction) génèrent des déformations de la Terre ; ces écarts s'appellent force de marée et intéressent les géophysiciens et géodésiens.
Il y a ainsi une première façon de présenter la force de marée : la force de marée correspond à l'écart à la moyenne de l'attraction de la Lune c'est-à-dire à l'écart entre attraction de la Lune en un point et attraction moyenne sur la Terre.
La deuxième façon de voir la force de marée demande plus de connaissances en mécanique mais elle explique pourquoi on retranche la valeur moyenne de l'attraction lunaire. La force de marée correspond à l'effet de l'attraction de la Lune vue dans un référentiel géocentrique, c'est-à-dire à l'effet de l'attraction de la Lune en ajoutant la force apparente d'entraînement liée au mouvement orbital de la Terre.
Listons les forces ressenties par un observateur situé en un point de la Terre :
- l'attraction de la Terre,
- la force centrifuge liée à la rotation de la Terre autour de l'axe des pôles,
- la force de Coriolis, si le point est en mouvement,
- l'attraction de la Lune,
- une force d'entraînement uniforme.
Les deux premières constituent ensemble la pesanteur ; les deux dernières la force de marée. Essayons de comprendre ce qu'est la force d'entraînement.
La Terre a tendance à tomber sur la Lune mais, puisqu'elle possède une vitesse orbitale, elle est en même temps écartée de la Lune, ce qui fait qu'en terme de trajectoire elle ne tombe pas vraiment et décrit une courbe quasi-circulaire [Terre-Lune]. Puisque la Terre ne tombe pas sur la Lune on peut dire qu'il existe une "force" qui contrebalance l'attraction lunaire. Cette force apparente est, comment on vient de le voir, liée au mouvement : c'est l'opposée de l'accélération de la Terre (multipliée par sa masse) dans le référentiel galiléen 𝓡.
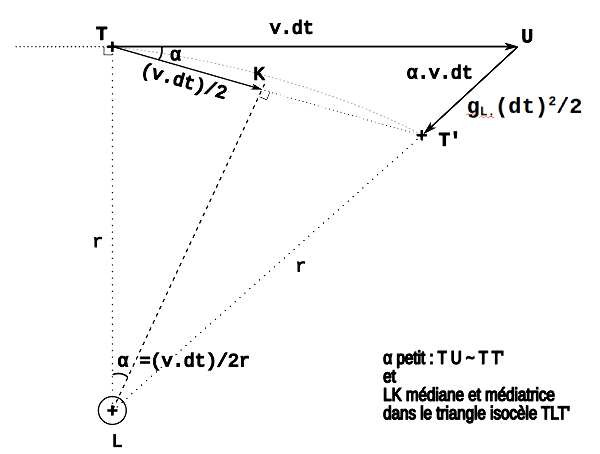
S'il n'y avait pas l'attraction de la Lune, pendant un temps dt la Terre parcourrait une distance v.dt en ligne droite. Avec l'attraction lunaire, pendant ce même laps de temps, elle tombe aussi sur la Lune de la distance gL(dt)2/2 (figure). Or, on peut calculer cette longueur de chute d'une autre façon : pour des petits angles, l'angle de déviation de la trajectoire α est tel que α = v.dt/2r, de plus la trajectoire est quasi circulaire ce qui indique que la longueur de chute est α.v.dt = (v.dt)2/2r. C'est ainsi que Newton a montré la relation bien connue gL = v2/r (attraction égale accélération centripète). Et qu'il a découvert ce que raconte l'histoire de la pomme : la Lune tombe vers la Terre suivant les mêmes principes que la pomme.
Mettons cela en équation. Notons l'attraction moyenne de la Lune sur la Terre[3], la masse de la Terre et l'accélération du centre T de la Terre dans le référentiel galiléen 𝓡. Le principe fondamental de la dynamique, , peut aussi s'écrire :
On peut donc voir le mouvement comme un équilibre où le terme est une force apparente.
Chacun a déjà ressenti cette équivalence entre accélération et force dans une voiture qui prend un virage : l'accélération centripète de la voiture est ressentie comme une force centrifuge par le passager. Chacun des deux points de vue fait référence à un référentiel d'observation : dans un référentiel galiléen la somme des forces est égale au produit de la masse par l'accélération alors que dans le référentiel mobile, l'accélération de ce référentiel est perçue comme une force, de sens opposé, qu'on appelle force d'entraînement.
Le raisonnement que nous venons de tenir pour la Terre globale s'applique en partie à toute particule liée à la Terre. Une masse située en un point subit l'attraction de la Lune mais aussi la force d'entraînement . La somme de ces deux attractions s'appelle force de marée :
- .[4]
Par commodité on définit alors l'accélération de marée :
Décrivons un peu plus l'accélération d'entraînement . Dans la marée, on ne s'intéresse pas à la rotation de la Terre sur elle-même, celle-ci est contenue dans la pesanteur. On cherche donc la force dans un référentiel dont les axes ont des directions fixes ; dans un tel référentiel tous les points ont une même accélération : est donc uniforme (ne dépend pas du point ). Ce n'est donc pas, comme on le lit parfois, une force centrifuge (qui n'est pas uniforme), mais une force inertielle de translation non rectiligne.
Si la Terre est sphérique l'attraction moyenne est égale à l'attraction au centre de la Terre . Dans la plupart des livres, on confond d'emblée les deux, ce qui est une approximation très satisfaisante. C'est ce que nous ferons aussi désormais.
Amplitude et direction de la force de marée
L'ordre de grandeur de la force de marée est facile à estimer en faisant la différence des deux forces d'attraction entre le point proche de la Lune et le centre de la Terre :
- .
C'est la différentielle d'une fonction en , c'est donc une fonction proportionnelle à .
Pour connaître complètement la force il nous faut son amplitude et sa direction partout.
Par le dessin tout d'abord, les deux forces qui composent la marée se déterminent aisément (figures ci-dessous) : nous voyons que la force de marée a tendance à allonger la Terre dans la direction Terre-Lune, à la comprimer dans le plan perpendiculaire et à créer ainsi deux "bourrelets".
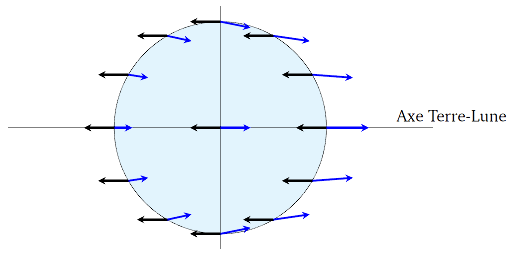
Figure 2. Accélérations d'attraction de la Lune et d'inertie de translation
L'accélération d'attraction de la Lune (, bleu) pointe vers la Lune et est d'autant plus grande que le point est proche de la Lune. L'accélération d'inertie de translation est, elle, uniforme () et égale en norme à au centre de la Terre. Les vecteurs sont représentés en différents points d'un plan contenant l'axe Terre-Lune.
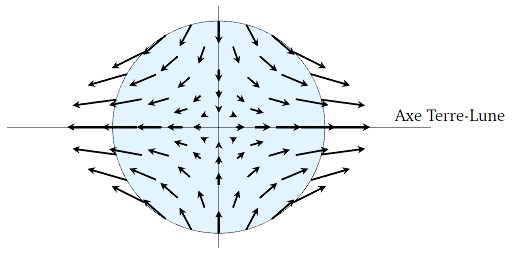
Figure 3. Accélération de marée
L'accélération de marée (c'est-à-dire la somme des flèches bleues et noires de la figure précédente) en différents points d'un plan contenant l'axe Terre-Lune est à symétrie de révolution autour de l'axe Terre-Lune et symétrique par rapport au plan perpendiculaire à cet axe et passant par le centre de la Terre.
Mathématiquement, on peut montrer que l'accélération de marée dérive d'un potentiel de marée () qui a la forme :
- [4],
où est la distance de au centre de la Terre, et où est sa distance zénithale avec la Lune, c'est-à-dire l'angle au centre de la Terre , angle entre la direction de la Lune (TL) et celle du point M (TM).
Plan de l'exposé
Cinq notes constituent cet exposé sur les marées :
Une partie de cet ensemble de notes sur les marées reprend des articles rédigés avec Étienne Ghys pour le site internet des Mathématiques pour la Terre – 2013.
[1] Un référentiel galiléen, ou inertiel, est un référentiel dans lequel un objet isolé (sur lequel ne s'exerce aucune force ou sur lequel la résultante des forces est nulle) est en mouvement de translation rectiligne uniforme.
[2] La résultante (somme) de l'attraction sur la Terre divisée par sa masse.
[3] Mathématiquement .
[4] Le signe := signifie que l'égalité est une définition.