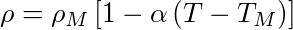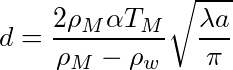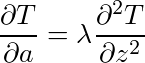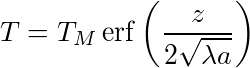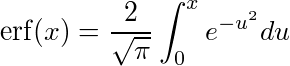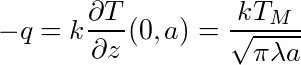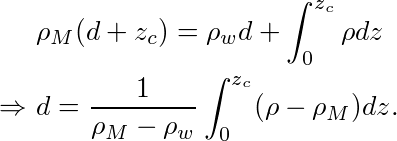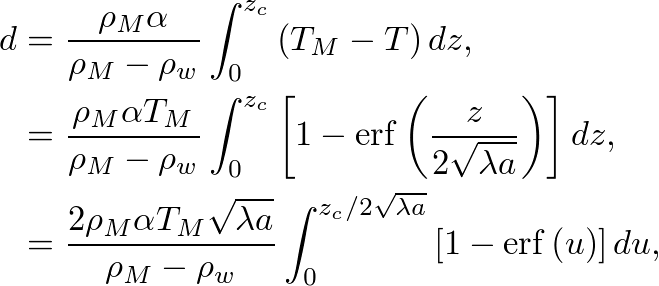Article | 12/03/2009
Géophysique des fonds océaniques
10/03/2009
Résumé
L'évolution des fonds océaniques avec leur âge : théorie, flux de chaleur associé et profondeur du plancher océanique.
Table des matières
Article mis à jour le 16 septembre 2009.
Cet article présente la théorie de l'évolution des fonds océaniques avec leur âge qui permet d'expliquer les observations géophysiques. Une attention particulière est apportée au flux de chaleur océanique dont on montre que les mesures de bonne qualité sont bien expliquées par la théorie. On peut donc appliquer la théorie dans les régions où aucune mesure n'a été faite, du moment que l'on connaît l'âge de la lithosphère. Les mesures du magnétisme sous-marin, qui ont d'abord permis de prouver l'ouverture océanique, servent depuis à déterminer l'âge des fonds océaniques, et donc le flux de chaleur. C'est de cette façon que l'on détermine la perte de chaleur de la Terre au travers de sa lithosphère océanique.
Une autre observation importante concerne la profondeur du plancher océanique. En faisant l'hypothèse d'isostasie, le modèle de température dans la lithosphère permet de prédire l'évolution de cette profondeur avec l'âge et, là encore, l'accord entre prédiction du modèle et observation est excellent.
Introduction
Les observations des fonds océaniques ont permis de démontrer l'ouverture océanique et la tectonique des plaques. C'est dans ce contexte que de nombreuses observations des fonds océaniques ont été depuis interprétées. Cet article concerne notamment le flux de chaleur et la profondeur du plancher océanique. Ce dernier point permet également d'expliquer l'évolution des îles de point chaud, de leur formation comme île haute volcanique à leur évolution en atoll (ce qui sera traité dans un article ultérieur).
Un modèle de refroidissement de la lithosphère
La lithosphère, par définition, est la zone à la surface de la Terre qui se comporte de manière rigide (de lithos, pierre en grec). La raison de cette rigidité, par opposition à la faible rigidité de l'asthénosphère, provient de sa faible température. En effet, la viscosité des roches du manteau dépend fortement de la température, et celle–ci est plus faible près de la surface. C'est ce qui confère cette rigidité à la lithosphère. Pour comprendre les fonds océaniques il est donc nécessaire de s'intéresser à la température. Plus généralement, on considère maintenant que la lithosphère océanique est la couche limite supérieure de la convection dans le manteau, dont les variations de température sont le moteur.
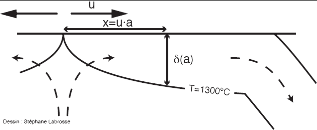
Figure 1. Modèle schématique de lithosphère océanique
À partir de la dorsale médio–océanique où la matière arrive chaude vers la surface (ce qui induit de la fusion partielle par décompression et produit la croûte océanique), un refroidissement se produit par contact avec l'eau de mer. La zone froide est très visqueuse et forme la lithosphère. La diffusion thermique permet au front froid de se propager vers le bas, ce qui mène à l'épaississement de la lithosphère.
Pour calculer la température dans la lithosphère océanique, le principe est expliqué sur la figure 1. La croûte océanique est formée par fusion due à la décompression de la matière mantellique chaude qui arrive près de la surface au niveau de la dorsale médio–océanique. Au contact avec l'eau de mer, la matière (croûte et manteau sous-jacent) se refroidit en même temps qu'elle se déplace horizontalement. Le front froid (matérialisé sur le schéma par l'isotherme 1300°C, on verra plus loin pourquoi), inexistant près de la dorsale où le volcanisme est actif, se propage vers le bas lorsque l'on s'éloigne de la dorsale. Cet enfoncement se produit par diffusion thermique et dépend du temps écoulé depuis la formation de la lithosphère à la dorsale. Ce problème est similaire à celui du refroidissement de la Terre tel que formulé par Fourier et Kelvin et sa solution est bien connue (voir Calculs / Flux de chaleur). On trouve que le flux de chaleur q varie avec l'âge du fond océanique a (le temps écoulé depuis la formation de la croûte à la dorsale)
avec TMla température du manteau sous la lithosphère (en degrés Celsius), k la conductivité thermique et λ la diffusivité thermique.
La conductivité thermique est le paramètre physique permettant de relier le flux de chaleur au gradient de température, via la loi de Fourier ; la diffusivité thermique caractérise la vitesse de changement de la température par diffusion.
Il s'agit maintenant de tester cette théorie par comparaison avec les observations terrestres.
Comparaison avec les données de flux de chaleur
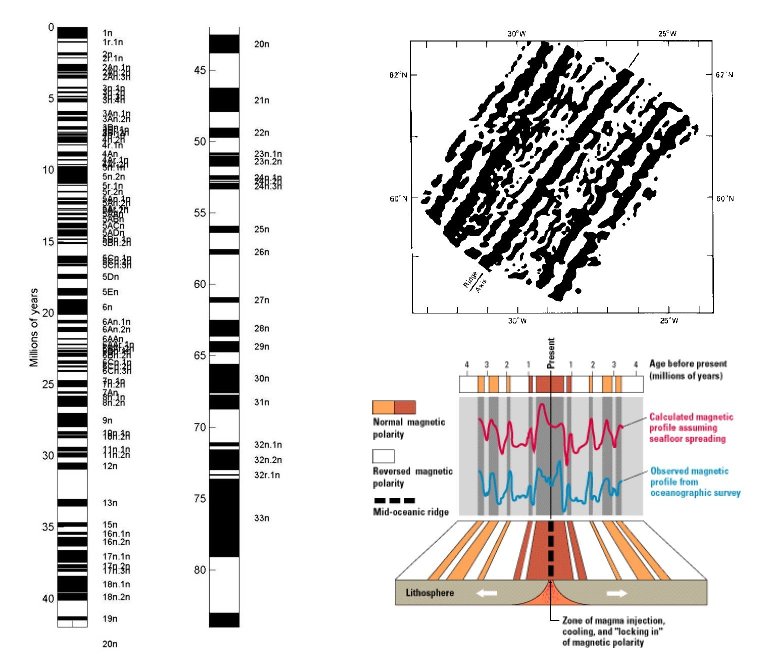
Figure 2. Le code barre des fonds océaniques
À gauche, les âges des transitions entre périodes de polarité normale (c'est-à-dire identique au temps présent, en noir) et les périodes inverses (en blanc) donnés par Cande & Kent (1995). La succession de ces périodes se retrouve dans l'aimantation du plancher océanique (observations en haut à droite, d'après Vine (1966) et modélisation en bas à droite, d'après Kious et Tilling (1996)) et on peut ainsi dater les fonds océaniques en faisant correspondre les limites de polarité observées (en haut à droite) avec celles données dans l'échelle des âges (gauche).
Pour comparer la prédiction de l'équation (1) avec les observations, il faut mesurer le flux de chaleur et l'âge de la lithosphère aux mêmes points. La détermination de l'âge d'une roche utilise souvent des méthodes radiométriques, mais cela n'est guère pratique pour les fonds océaniques. On utilise en fait le magnétisme et la compréhension que l'on a de l'expansion océanique. On se rappelle en effet que c'est la découverte des bandes de polarité magnétique successivement normale et inverse et leur enregistrement continu dans la lithosphère océanique qui ont permis de démontrer sans équivoque l'ouverture océanique, en interprétant ces inversions à la lumière des inversions découvertes bien avant dans des séries volcaniques continentales. La succession irrégulière des inversions du champ magnétique permet en outre de dater les fonds océaniques. Les datations radiochronologiques des inversions du champ magnétiques ont permis de construire une échelle des temps, véritable “code–barre” qui, par comparaison avec le champ magnétique crustal du plancher océanique (figure 2), permet de dater ces fonds. La figure 3 montre le résultat sous forme de carte d'un tel travail.
Source - © 2008 EarthByte.org, Licence Creative Commons BY
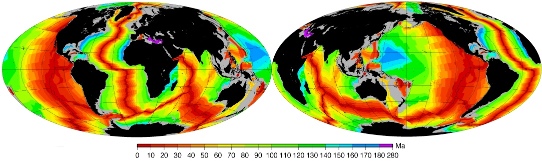
Figure 3. Cartes des âges (en millions d'années, Ma) des fonds océaniques obtenus par le magnétisme
Données tirées de Müller et al. (2008) et disponible sur le site www.earthbyte.org
Projections Hammer, centrée sur le méridien 0° (gauche) et 180° (droite).
Cartes individuelles : âge des fonds océaniques (0°) ; âge des fonds océaniques (180°).
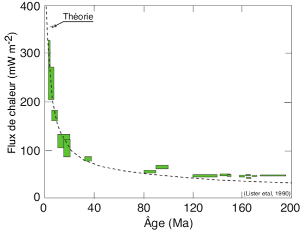
Maintenant que l'on connaît l'âge des fonds océaniques, il nous faut déterminer le flux de chaleur. Celui–ci est mesuré lors de campagnes océanographiques dédiées qui utilisent une sonde équipée de thermocouples et de résistances chauffantes que l'on enfonce dans les sédiments peu consolidés du plancher océanique. Cette sonde permet de mesurer au même point la conductivité thermique et le gradient vertical naturel de température (voir la page d'Alain Bonneville (IPGP) pour plus de détails). Le flux de chaleur est alors obtenu en utilisant la loi de Fourier (première partie de l'équation (8)). On peut alors collecter toutes les données obtenues et les classer par ordre d'âge du plancher océanique. La figure 4 représente le résultat d'une telle compilation et montre le bon accord entre la théorie donnée par l'équation (1) et les observations. Plusieurs paramètres libres dans l'équation nécessitent un ajustement, en particulier la température : le résultat est la ligne pointillée de la figure. Cela permet de contraindre la température du manteau sous la lithosphère qui doit être d'environ 1300°C.
Figure 4. Compilation des données de flux chaleur océanique en fonction de l'âge de la croûte
Chaque boite représente la variabilité des données dans la tranche d'âge considérée. La ligne pointillée est un ajustement selon l'équation (4).
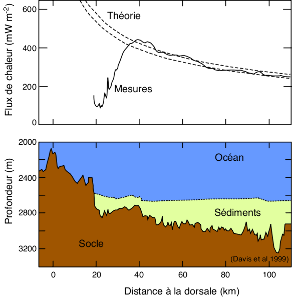
Une vérification directe de la théorie peut également être faite lors d'une campagne de mesures. La figure 5 montre les résultats d'une telle campagne, effectuée à proximité de la dorsale Juan de Fuca (Pacifique Nord-Est). On voit que les mesures suivent très bien la théorie, représentée avec son incertitude par les deux lignes pointillées, là où la couverture sédimentaire est suffisante pour que les mesures soient de bonne qualité.
Près de la dorsale, les mesures et la théorie ne "collent" pas. En effet (1) les mesures sont difficiles car il y a peu de sédiments et (2) la chaleur est évacuée par circulation hydrothermale, avec sortie par les "fumeurs" et non pas de façon homogène sur le fond océanique.
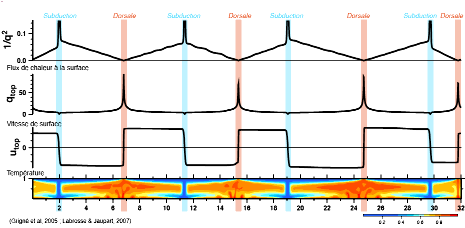
Enfin, on peut comparer cette théorie et ces observations à des résultats numériques de modèles de convection. La figure 6 montre de tels résultats (Grigné et al., 2005; Labrosse et Jaupart, 2007).
Figure 6. Résultat de modèle de convection dans le manteau
La partie basse représente la température dans le domaine de calcul et les courbes supérieures montrent la vitesse de surface (utop), le flux de chaleur à la surface (qtop) et l'inverse de son carré (1/q2).
Le calcul est ici réalisé en deux dimensions, c'est-à-dire qu'il représente une tranche du système complet. La partie basse de la figure représente la température (en unité arbitraire entre 0, en bleu, et 1, en rouge) et montre bien, en bleu, une lithosphère froide qui s'épaissit en s'éloignant de la dorsale, et qui finit par subducter. La courbe donnant le flux de chaleur en surface montre bien une diminution lorsque l'on s'éloigne de la dorsale. La courbe donnant l'inverse du carré de ce flux de chaleur montre une évolution linéaire avec la distance à la dorsale, comme indiqué par l'équation 1. Ceci indique que la vitesse de surface ne varie pas tellement et que la théorie développée pour les fonds océaniques permet également d'interpréter les résultats de modèles numériques de convection.
Carte de flux de chaleur et perte totale
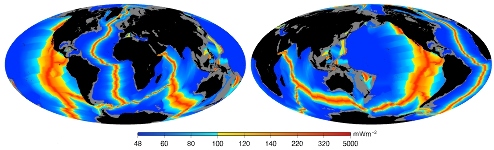
Ayant obtenu un bon accord entre théorie et observations du flux de chaleur, on peut utiliser la carte des âges des fonds océaniques (figure 3) pour calculer une carte de flux de chaleur, avec la formule
avec q le flux en mW.m-2 en et a l'âge en millions d'années (Ma). Le coefficient Cq = 490 ± 20 provient de l'ajustement fait sur la figure 4. On obtient alors la figure 7 où l'on voit que le flux de chaleur sortant au niveau des dorsales peut être très important, comme cela est directement mesuré lorsque la couverture sédimentaire est suffisante (figure 5). À partir de cette carte, on peut calculer le flux de chaleur total extrait de la Terre au travers des fonds océaniques et on obtient 30 TW (térawatts), c'est-à-dire 30x1012 W. À cette valeur, il faut ajouter le flux de chaleur au niveau des points chauds (non pris en compte ici), environ 2 TW, le flux continental, environ 14 TW, ce qui fait un total de 46 TW.
Figure 7. Flux de chaleur océanique calculé à partir de la carte des âges du plancher océanique
Deux dorsales majeures apparaissent pour le flux de chaleur : la dorsale pacifique et la dorsale est-indienne.
Projections Hammer, centrée sur le méridien 0° (gauche) et 180° (droite).
Cartes individuelles : flux de chaleur océanique (0°) ; flux de chaleur océanique (180°).
Flux de chaleur calculé (S. Labrosse) à partir de la carte des âges selon l'équation (2).
Visionnez le flux de chaleur océanique sur Google Earth, téléchargez le kmz flux de chaleur océanique.
Profondeur du plancher océanique
Source - © 2009 Topex / Univ. California San Diego
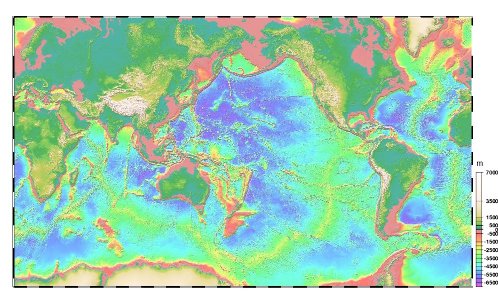
Figure 8. Topographie des continents et des océans
On voit bien les dorsales océaniques qui forment une chaîne de montagnes sous-marine. En s'en éloignant perpendiculairement, la profondeur augmente.
Une autre observation importante concerne la profondeur du plancher océanique, qui augmente avec la distance à la dorsale (figure 8). Comme on l'a vu pour le flux de chaleur, la distance à la dorsale ne semble pas être la variable la plus pertinente et il semble plus raisonnable de considérer la variation de la profondeur en fonction de l'âge du plancher océanique, ou mieux encore, la racine de cet âge.
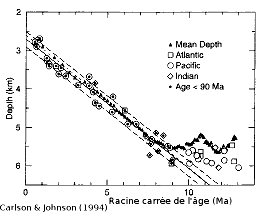
La figure 9 montre justement une compilation de telles données, océan par océan et en moyenne globale. On voit qu'effectivement la profondeur augmente linéairement avec la racine carrée de l'âge, jusqu'à un âge d'environ 80 millions d'années, âge à partir duquel la profondeur n'augmente plus. On peut d'ailleurs remarquer que cela correspond également à l'arrêt de la variation du flux de chaleur avec l'âge sur la figure 4. Cet écart entre théorie et observation est généralement interprété comme étant dû au démarrage d'une convection à petite échelle sous la lithosphère mais cela de sera pas discuté ici. Pour la plus grande partie du plancher océanique, l'approfondissement proportionnel à la racine carrée de l'âge est observé et nécessite une explication.
La raison pour laquelle le plancher océanique voit sa profondeur augmenter avec l'âge est liée à son évolution thermique, telle que décrite plus haut. Lorsque la température baisse, la matière généralement se contracte, où encore sa masse volumique (ou sa densité) augmente. Il s'agit du mécanisme moteur pour la convection thermique : lorsque la matière refroidit à la surface de la Terre, elle devient plus dense que le manteau asthénosphérique sous-jacent et elle finit par plonger. Ce phénomène de contraction thermique (ou de dilatation dans le cas de l'opération inverse) est quantifié par un paramètre thermodynamique appelé coefficient de dilatation thermique, α. En utilisant la température du manteau asthénosphérique, TM, comme référence, on écrit la variation de masse volumique avec la température comme
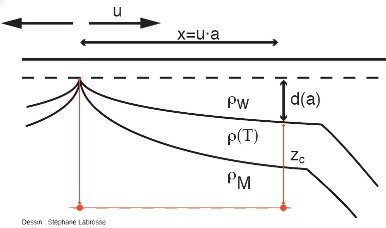
u étant la vitesse du mouvement de la plaque (la demi-vitesse d'ouverture de la dorsale), on se place à une distance x=u.a de la dorsale, sur une lithosphère d'âge a. La profondeur du plancher est supérieure de d(a) à celle de la dorsale. La densité de l'eau ρw est supposée constante, alors que la densité de la lithosphère, ρ(T), diminue avec la température, T, jusqu'à atteindre ρM, la densité du manteau asthenosphérique.
Le niveau horizontal rouge, situé sous la lithosphère, est le niveau de compensation.
En se refroidissant, la plaque lithosphérique voit sa densité augmenter, ce qui induit une déformation du manteau sous-jacent. Le plancher s'enfonce de façon à ce que la masse d'une colonne verticale soit identique en tout point d'une surface appelée profondeur ou niveau de compensation (voir Calculs / Isostasie). C'est ce qu'on appelle l'isostasie. On note d(a) la différence de profondeur de l'océan entre la dorsale (âge nul) et celle à l'âge a (figure 10), et ρw la masse volumique de l'eau. En combinant l'équation (3) avec l'équation (6), l'équilibre isostatique donne :
On explique ainsi l'augmentation de la profondeur comme la racine carrée de l'âge du fond océanique.
Conclusion
On a vu que, dans le cadre de la tectonique des plaques, on peut développer une théorie de l'évolution thermique de la lithosphère océanique qui concorde avec les observations du flux de chaleur et de la profondeur du plancher océanique. Ceci permet de déterminer la part des océans dans la perte de chaleur de la Terre. La tectonique des plaques est l'expression de surface de la convection dans le manteau et la lithosphère doit être considérée comme la couche limite froide de la convection dans le manteau. Pour le transfert de chaleur dans les continents, d'autres approches sont nécessaires et l'ensemble permet d'obtenir un flux de chaleur total de 46 TW (dont 30 TW pour les fonds océaniques). Ceci permet alors de calculer l'évolution thermique de la Terre. Une présentation détaillée est données par Jaupart et al. (2007) (pdf disponible).
Équations et détails des calculs
Température dans la lithosphère et flux de chaleur
Si l'on suit le mouvement de la plaque, et en négligeant les variations horizontales de température par rapport aux variations verticales, la température satisfait l'équation de la diffusion à une dimension (la variation de température en fonction de l'âge dérive du gradient de température en fonction de la profondeur) :
avec a l'âge de la lithosphère (c'est-à-dire le temps écoulé depuis sa création au niveau de la dorsale), z la profondeur et λ la diffusivité thermique, ayant pour unité le m2.s-1. En analysant les dimensions de l'équation (5), on voit que la profondeur δ du front froid ne peut qu'être proportionnelle à √(λa). En prenant l'âge maximum de la lithosphère océanique, 180 Ma, et une diffusivité thermique λ=10-6 m2.s-1, on trouve une épaisseur maximale de lithopshère océanique de l'ordre de δmax≃75 km. Cette épaisseur est faible par rapport à l'épaisseur du manteau et on considère donc un milieu semi-infini. Pour résoudre le problème, il faut ajouter une condition initiale et des conditions limites. Au niveau de la dorsale (a=0), la température est considérée comme uniforme, égale à TM. Cette température est aussi la température pour z→∞. À la surface, le contact avec l'océan maintient la température à une valeur constante de l'ordre de 2°C (que l'on prendra égale à 0, pour simplifier). La solution à ce problème est connue depuis Fourier :
La fonction erf intervenant, appelée “fonction erreur”, est définie comme
Il s'agit du géotherme utilisé par Kelvin (Thomson, 1862) pour calculer l'âge de la Terre. Le flux de chaleur en surface est obtenu en prenant le gradient vertical à la surface, que l'on multiplie par la conductivité thermique, k, (Loi de Fourier) :
Le signe négatif est introduit pour que -q soit le flux dans la direction des z décroissants, c'est-à-dire vers l'extérieur de la Terre. On a ainsi obtenu une expression du flux de chaleur océanique en fonction de l'âge de la lithosphère.
Calcul de l'équilibre isostatique
L'équilibre isostatique postule que la pression à une profondeur dite de compensation est indépendante de l'âge. En supposant que cette pression est hydrostatique, elle est égale au poids de la matière au-dessus de cette profondeur de compensation. En écrivant cette égalité pour les deux points figurés en rouge sur la figure 10, on obtient (avec des densités constantes on ferait une simple somme, la densité variant avec la profondeur on doit intégrer) :
L'écart entre la densité en profondeur (ρM) et celle (ρ) qui dépend de la température dans la listhosphère est obtenue en utilisant l'équation (3), dans laquelle la température donnée par l'équation (6) est utilisée :
où l'on a fait un changement de variable pour obtenir la dernière égalité. Comme la variation de température, et donc de masse volumique, n'est importante que dans la lithosphère, c'est-à-dire près de la surface, toute valeur de zc supérieure à l'épaisseur de la lithosphère donne un résultat similaire et on peut calculer l'intégrale en prenant zc→∞. L'intégrale de la fonction erreur de 0 à l'infini est connue et on obtient l'équation (4) donnant la variation de profondeur d du plancher océanique en fonction de l'âge a de la lithosphère.
Références
S.C. Cande, D.V. Kent, 1995. Revised calibration of the geomagnetic polarity timescale for the late cretaceous and cenozoic, J. Geophys. Res., 100, 6093–6095
R.L. Carlson, H.P. Johnson, 1994. On modeling the thermal evolution of the oceanic upper-mantle: An assessment of the cooling plate model., J. Geophys. Res., 99, 3201–3214
E.E. Davis, D.S. Chapman, K. Wang, H. Villinger, A.T. Fisher, S.W. Robinson, J. Grigel, D. Pribnow, J. Stein, K. Becker, 1999. Regional heat flow variations across the sedimented Juan de Fuca Ridge eastern flank: Constraints on lithospheric cooling and lateral hydrothermal heat transport, J. Geophys. Res., 104, 17675–17688 [pdf]
C. Grigné, S. Labrosse, P.J. Tackley, 2005. Convective heat transfer as a function of wavelength: Implications for the cooling of the Earth., J. Geophys. Res., 110, B03409
C. Jaupart, S. Labrosse, J.-C. Mareschal, 2007. Treatise of Geophysics. Mantle dynamics, Elsevier, vol. 7, chap. 6, 253–303, Temperatures, Heat and Energy in the Mantle of the Earth
J.W. Kious, R.I. Tilling, 1996.This Dynamic Earth - The Story of Plate Tectonics, DIAME Publishing, 77p
S. Labrosse, C. Jaupart, 2007. Thermal evolution of the Earth: Secular changes and fluctuations of plate characteristics., Earth Planet. Sci. Lett., 260 , 465–481
C.R.B. Lister, J.G. Sclater, E.E. Davis, H. Villinger, S. Nagihara, , 1990. Heat flow maintained in ocean basins of great age: investigations in the north-equatorial West Pacific., Geophys. J. Int., 102, 603–628
R.D. Müller, M. Sdrolias, C. Gaina, W.R. Roest, , 2008. Age, spreading rates, and spreading asymmetry of the world's ocean crust, Geochem. Geophys. Geosyst., 9
W. Thomson (Lord Kelvin), 1862. On the secular cooling of the earth, Trans. Roy. Soc. Edinburgh, 23, 295–311
J.F. Vine, 1966. Spreading of the ocean floor: new evidence, Science, 154, 3755, 1405-1415 [pdf]