Article | 16/05/2012
Déterminer la latitude d'un lieu
18/05/2012
Résumé
Quelques méthodes simples de détermination de la latitude d'un lieu par l'observation du Soleil (hauteur et durée du jour) ou des étoiles (hauteur lors de la culmination).
Table des matières
Aujourd'hui, pour connaître la latitude d'un lieu, il suffit d'allumer son GPS et la valeur s'affiche immédiatement sur l'écran. Mais avant l'arrivée du GPS, quelles étaient les techniques possibles ? Il en existe beaucoup. Certaines utilisent la course du Soleil dans le ciel et d'autres, la course des étoiles. Nous n'en présenterons que quelques-unes, les plus simples. Pour le Soleil, avec un simple "bâton", nous pourrons déterminer la plus grande hauteur du Soleil au cours de la journée et avec une montre, la durée du jour. Cela nous donnera deux techniques différentes pour déterminer la latitude d'un lieu. Pour les étoiles, nous mesurerons avec un théodolite d'occasion, leur hauteur au moment où elles culminent et cela nous donnera de nouvelles méthodes.
Ce travail a été réalisé avec trois élèves de première scientifique du lycée Jean Monnet d'Annemasse (Corentin Puffay, Garance Sarton et Émile Séchaud), qui ont gagné le premier prix des Olympiades de physique 2012.
Deux notions préalables
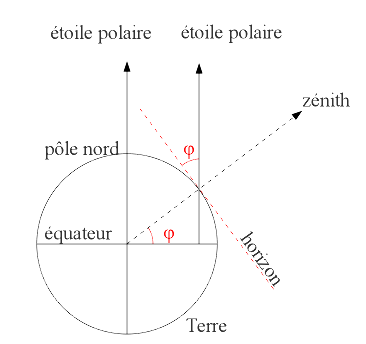
La hauteur du pôle
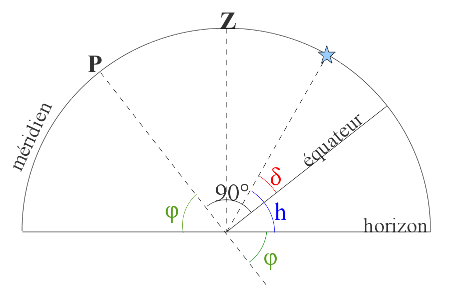
La latitude d'un lieu est l'angle que fait la verticale du lieu avec le plan équatorial. C'est également la hauteur du pôle céleste (approximativement représenté par l'étoile polaire dans l'hémisphère Nord) au-dessus de l'horizon (figure ci-dessous).
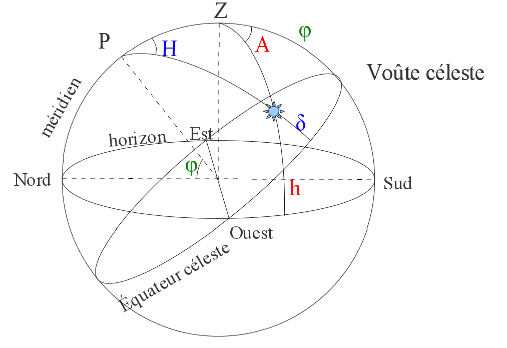
Les coordonnées d'un astre
Si l'on considère que le ciel est comme une voûte sphérique entourant le lieu d'observation, repérer un astre consiste à déterminer deux angles pour le positionner à la surface d'une sphère (figure ci-dessous).
- Dans le système des coordonnées horizontales, l'astre est repéré par sa hauteur h au-dessus de l'horizon (angle entre la direction de l'astre et le plan horizontal) et par son azimut A (angle entre la direction du méridien – le Sud, dans l'hémisphère Nord – et la direction de l'astre dans le plan horizontal).
- Dans le système des coordonnées horaires, l'astre est repéré par sa déclinaison δ au-dessus de l'équateur céleste (angle entre la direction de l'astre et le plan équatorial) et par son angle horaire H, qui est la durée qui sépare son passage au méridien de sa position actuelle.
Figure 2. Repérage d'un astre sur la voûte céleste entourant le lieu d'observation (au centre)
P est le pôle céleste, Z le zénith, φ la latitude du lieu. Le repérage d'un astre dans le ciel se fait grâce aux coordonnées horizontales hauteur (h) et azimut (A) et/ou aux coordonnées horaires déclinaison (δ) et angle horaire (H).
Détermination de la latitude d'un lieu avec le Soleil
Pour déterminer une latitude avec le Soleil, on peut utiliser sa hauteur lorsqu'il passe au méridien du lieu, c'est la méthode la plus connue. On peut également utiliser la durée du jour (ou encore l'azimut du coucher).
Latitude et hauteur du Soleil à midi (utilisation du gnomon)
Le gnomon est sans doute le plus vieil instrument astronomique. Il s'agit d'une tige verticale plantée dans le sol, dont on étudie l'ombre au cours de la journée et au cours de l'année. La direction de l'ombre sert à déterminer l'heure, la longueur de l'ombre comparée à celle de la tige à calculer la hauteur du Soleil.
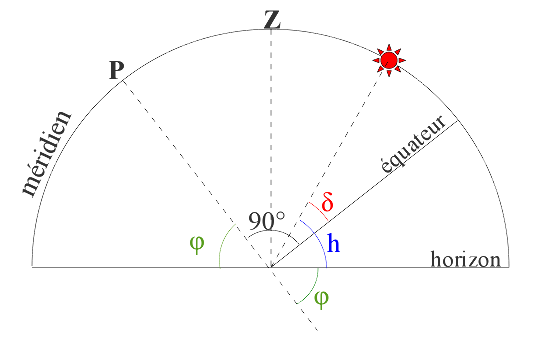
Figure 3. Hauteur du Soleil dans le plan méridien
La figure est réalisée dans le plan méridien (grand cercle qui passe par le zénith du lieu et le pôle céleste et qui est donc orienté Nord-Sud). Lors de leur trajectoire quotidienne dans le Ciel, les astres culminent (atteignent leur plus grande hauteur) lorsqu'ils passent dans le méridien.
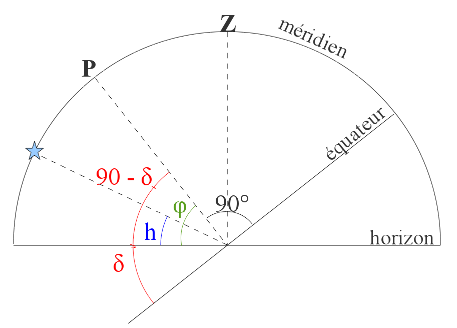
D'après la figure ci-dessus, on peut établir la relation suivante : φ = 90° + δ - h.
Si on connaît δ (en allant sur le site de l'IMCCE – Institut de Mécanique Céleste et de Calcul des Éphémérides) et si on mesure h avec l'ombre d'un gnomon, on peut trouver φ.
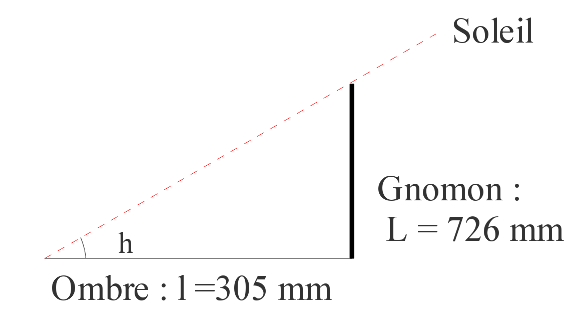
La mise en place du dispositif demande d'être assez méticuleux. Pour avoir une plateforme parfaitement horizontale, nous avons placé des cales sous une grande planche dont nous avons vérifié l'horizontalité grâce au niveau à bulles. Pour être sûr d'être perpendiculaire à la planche, nous n'avons pas utilisé un bâton vertical mais une planchette percée d'un trou et fixée à un trépied. Nous avons cherché le point à la verticale du trou grâce à un fil à plomb, ce qui nous permet également de mesurer la hauteur du gnomon, ici 726 mm. L'avantage du trou dans une planchette est que la tache lumineuse donne immédiatement la hauteur du centre du Soleil et non pas de son bord supérieur comme pour l'ombre d'un bâton.
Nos mesures ont été réalisées le 14 juin dans la cour du lycée. La déclinaison du Soleil est pour ce jour δ = 23°14'59,8'' ~ 23,25°
La hauteur du Soleil est calculée par : tan(h) = 726/305 soit h = 67,21°.
La formule φ = 90° + δ - h donne φ = 90 + 23,25 - 67,21, soit φ = 46,04° = 46°2'24'': . Sur le site géoportail de l'IGN, on trouve la véritable latitude du lycée, φ = 46°10'54''. Notre détermination est donc trop basse de 8'30'' = 0,14° (la hauteur du Soleil déterminée est trop grande). L'erreur peut provenir de la réfraction atmosphérique, qui relève les objets visés. Mais pour une hauteur de 67° environ, la réfraction ne provoque qu'une surestimation de la hauteur de 30''. Il est clair que la cause principale de notre erreur est l'incertitude de nos mesures de la hauteur du gnomon et de la longueur de l'ombre.
Latitude et durée du jour
La durée du jour change en fonction de l'époque de l'année, elle change aussi en fonction du positionnement à la surface de la Terre. Ainsi, il existe un lien entre durée du jour et latitude et c'est ce lien qu'il faut expliciter. Pour ce faire, nous n'allons pas utiliser la trigonométrie sphérique, habituellement employée, mais uniquement la trigonométrie plane, grâce à des projections de la voûte céleste sur des plans (idée développée par Hipparque, il y a environ 2160 ans).
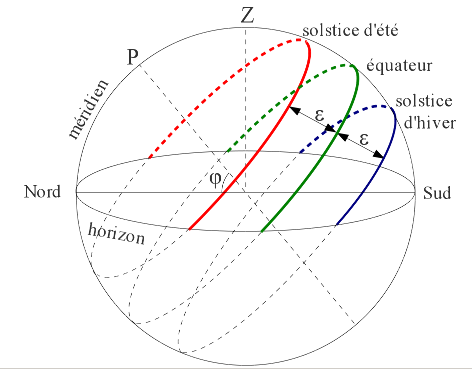
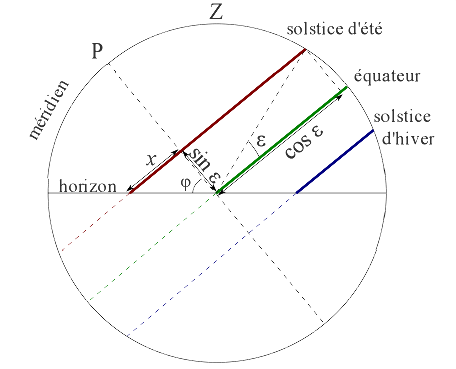
Figure 6. Trajectoires du Soleil sur la voûte céleste au solstice d'été, aux équinoxes et au solstice d'hiver Les trajectoires sont parallèles entre elles et perpendiculaires à l'axe de rotation. La latitude du lieu, φ, est l'angle entre le plan de l'équateur et le zénith du lieu, on retrouve donc aussi cet angle φ entre la direction du pôle céleste (perpendiculaire au plan de l'équateur) et l'horizon (plan perpendiculaire au zénith). | L'angle ε est l'obliquité de l'écliptique qui correspond à la déclinaison δ du Soleil au solstice d'été. On voit que le rayon du tropique d'été (trajectoire du Soleil au solstice d'été) est égal à cos ε. La portion de diamètre du tropique d'été correspondant au jour (partie en rouge, Soleil au-dessus de l'horizon) vaut cos ε + x. |
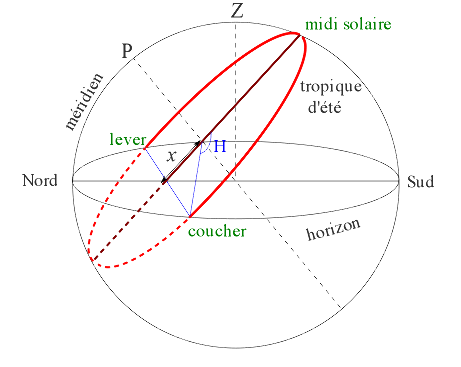
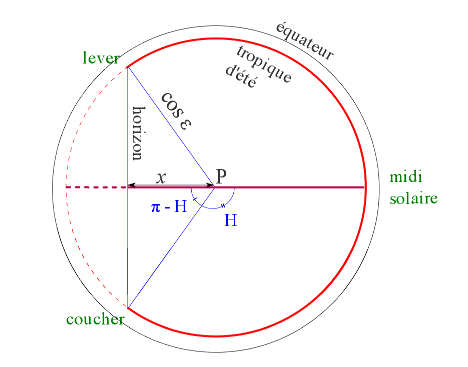
Figure 8. Détail de la trajectoire lors du solstice d'été L'angle H correspond à la moitié du jour (angle parcouru par le Soleil sur sa trajectoire entre son lever et midi, ou entre midi et son coucher). | Figure 9. Trajectoire du Soleil le jour du solstice d'été vu depuis le pôle céleste P Le rayon du tropique d'été est égal à cos ε (voir projection sur le plan méridien). |
Représentations de la trajectoire du Soleil pour déterminer le lien entre la durée du plus long jour et la latitude φ. La voûte céleste a pour rayon l'unité.
Dans la dernière figure (vue polaire), on voit que plus le jour est long, plus la valeur de x est grande.
On a la relation cos(π - H) = x / cos(ε), donc x = - cos(H).cos(ε).
Dans la deuxième figure (projection sur le plan méridien), on voit que plus x est grand, plus la latitude augmente.
On a la relation tan(φ) = x /sin(ε), donc x = tan(φ).sin(ε).
En confrontant les deux relations il vient, x = - cos(H).cos(ε) = tan(φ).sin(ε). Soit encore, cos(H) = - tan(φ).tan(ε)
Cette formule permet de calculer la latitude φ si on connaît H. Cette relation est établie pour le jour le plus long de l'année (lorsque la déclinaison du Soleil est égale à l'obliquité ε de l'écliptique). Pour un autre jour, il suffit de remplacer ε par la valeur de la déclinaison δ du Soleil.
Il s'agit de la maquette correspondant à la première figure du tableau ci-dessus. La graduation du cercle méridien permet de positionner le pôle céleste puis de lire directement la hauteur du Soleil aux solstices et aux équinoxes. La graduation de l'horizon donne accès à l'azimut du lever et du coucher et la graduation du disque correspondant au solstice d'été permet de déterminer la durée du plus long jour de l'année.
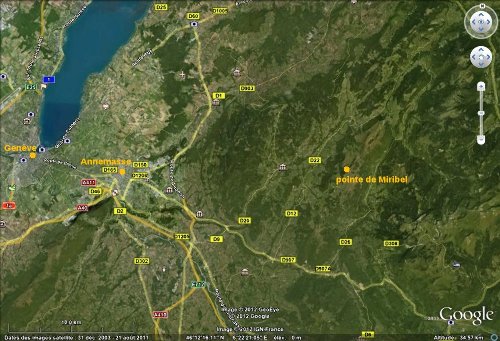
Nos observations ont été réalisées le soir du 27 juin et le matin du 28 au sommet de la Pointe de Miribel (46,212° N, 6,474° E). Pour ce jour, la déclinaison du Soleil est de 23,30° environ (c'est une valeur moyenne car la déclinaison varie continuellement). Le coucher a eu lieu à 21h30, le lever à 5h55. La durée du jour est donc de 15h35. L'angle horaire H du coucher du Soleil correspond à la moitié de la durée du jour, soit H = 7h47min30s = 7,792h. Dans les formules trigonométriques, il faut que H soit exprimé en degré. Pour faire la conversion, on sait que le Soleil fait un tour complet (360°) en 24h, on a donc : H = (7,792/24)x360 = 116,88°
On peut alors calculer la latitude correspondante : tan(φ) = - cos(116,88)/tan(23,3), soit φ = 46,40°
On est a 0,18° de la valeur véritable. Mais est-ce que notre valeur est fiable ? La durée du jour est en effet délicate à déterminer précisément : la réfraction, très forte près de l'horizon, relève le Soleil ; l'horizon n'est pas plan (surtout dans une région montagneuse !) ; il est difficile d'avoir l'heure exacte à laquelle le centre du Soleil se couche ou se lève. Une variation de 2,5min dans la valeur de H induit une variation de 0,6° dans la latitude ! Notre détermination à 0,18° près est donc certainement le résultat de plusieurs coïncidences qui se compensent.
Détermination de la latitude avec des étoiles
Figure 13. Théodolite, placé à la pointe de Miribel
Nous avons également voulu déterminer la latitude d'un lieu grâce à l'observation des étoiles. Il existe de très nombreuses méthodes ! On pensait pouvoir utiliser la hauteur de l'étoile polaire mais nous avons vu que cette étoile n'est pas exactement confondue avec le Pôle céleste : elle est à 0,68° du pôle. Il y a donc des corrections à faire et celles-ci sont compliquées. Nous avons uniquement appliqué les méthodes utilisant la hauteur des étoiles lorsqu'elles culminent (passage dans le méridien). Et nous avons mesuré cette hauteur grâce à un théodolite acheté d'occasion. L'avantage avec l'utilisation des étoiles est que l'on peut faire plusieurs mesures en une seule nuit et ainsi la détermination de la latitude repose sur une moyenne. Ce qui laisse espérer une plus grande précision car les erreurs peuvent se compenser. Pour préparer la nuit d'observation (toujours à la pointe de Miribel, le 27 juin – latitude 46,212°N), nous avons utilisé le logiciel Stellarium. Nous avons listé d'avance toutes les étoiles que nous voulions observer et l'horaire approximatif de leur passage au méridien.
Les étoiles peuvent passer au méridien entre l'horizon et le pôle (côté Nord), on parle alors de culmination inférieure. Elles peuvent aussi passer au méridien côté Sud, on parle alors de culmination supérieure. Pour la culmination supérieure d'une étoile, la situation est exactement similaire à celle que nous avons déjà vue pour le Soleil. Elle se modifie en revanche pour une culmination inférieure.
Figure 14. Culmination supérieure d'une étoile Pour une culmination supérieure : φ = 90 - h + δ. | Figure 15. Culmination inférieure d'une étoile Pour une culmination inférieure : φ = 90 + h - δ. |
Nous avons observé Antarès, des étoiles de la constellation du Serpentaire et de la Girafe (plus difficilement).
Figure 16. Mesures d'azimuts et résultats de calcul de latitude
Le zéro des azimuts est placé au Nord. Les mesures des azimuts et des hauteurs sont en grades. Les valeurs des déclinaisons sont reprises du logiciel Stellarium.
Les résultats sont décevants. Nous voulions obtenir une détermination de la latitude plus précise et nous obtenons des valeurs plus éloignées que celles trouvées avec le Soleil. Pour les étoiles qui culminent au Sud, la latitude est sous-estimée et pour celles qui culminent au Nord, elle est surestimée. Mais pour chaque groupe d'étoiles, les valeurs restent proches les unes des autres, et celles qui sont sous-estimées le sont d'autant que celles qui sont surestimées. Cela nous suggère une erreur systématique dans nos mesures de la hauteur des étoiles qui serait toujours trop forte de 1° environ. Nous avons peut-être fait une erreur dans la mise en place du théodolite (dans l'horizontalité de celui-ci). Il suffirait alors de refaire des observations pour obtenir des données plus adéquates. Mais malheureusement, en refaisant de nouvelles mesures, nous continuons d'obtenir une erreur de 1° environ. L'erreur systématique ne vient donc certainement pas de notre part mais d'une erreur d'étalonnage du théodolite, ou plutôt d'un dérèglement de celui-ci.
En prenant la moyenne entre les valeurs trouvées pour une étoile prise au Sud (Étoile 1) et une étoile prise au Nord (Étoile 2), il est possible d'éliminer cette erreur systématique car c'est alors la différence de leur hauteur qui intervient.
La latitude est donnée par : φ = 90 + (h2 - h1)/2 + (δ1 - δ2)/2
Si, de plus, les étoiles 1 et 2 ont des hauteurs à peu près identiques, cette moyenne élimine également l'influence de la réfraction atmosphérique. En utilisant deux couples d'étoiles différents, nous obtenons une latitude de 46,30°. Notre erreur est donc de 0,1°.
Pour conclure
Les méthodes pour déterminer la latitude d'un lieu sont donc très nombreuses. Et encore, nous n'avons présenté ici que les plus simples ou celles accessibles avec nos instruments (le théodolite, qui n'est pas l'instrument le plus approprié pour observer les étoiles, ne permet pas de mesures près du zénith). Celles que nous avons exposées sont faciles à mettre en œuvre et puisqu'elles ne demandent aucune connaissance en trigonométrie sphérique, elles sont abordables par des élèves de lycée.
Si des méthodes de détermination de la latitude sont connues depuis l'Antiquité et nécessitent une bonne maîtrise de la trigonométrie et des outils simples (mais pour lesquels l'obtention de valeur précises demande beaucoup de rigueur), la connaissance de la longitude fut aussi très importante. En effet, lors des grandes explorations (navigation sur les océans et prises de possession de territoires insulaires) la connaissance de la position exacte était indispensable pour se localiser et pouvoir revenir en un lieu précis. La détermination précise de la longitude fut historiquement plus difficile... mais c'est une autre histoire.