Article | 15/11/2001
Connaître le géotherme en profondeur
15/11/2001
Résumé
Détermination du géotherme, nécessité de couche limite thermique.
Table des matières
Question
« On représente souvent le géotherme terrestre avec une forte variation de température à 2900 km (température de 2000 °C à la base du manteau et au moins 3500°C à la limite supérieure du noyau)... Comment détermine-t-on ce saut de températures ? »
Question posée par D. P., le 17 novembre 2001, par courrier électronique.
Réponse
Nous n'avons aucune information directe sur la température à la base du manteau. Pas de mesures de température évidemment et pas d'échantillons non plus; il faut donc reposer sur des données indirectes.
L'apport de la sismologie à la connaissance du géotherme
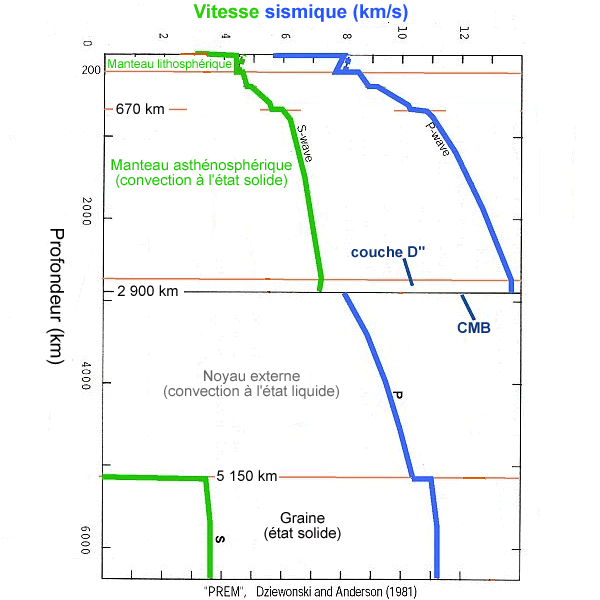
Les études de propagation des ondes sismiques à l'intérieur du globe montrent que le manteau est totalement solide. Il doit donc régner des températures qui permettent aux roches mantelliques soumises à des pressions de l'ordre de 130 GPa (giga Pascal) de ne pas fondre… Dans ces conditions, ces températures doivent être inférieures à 4.000 °C.
Figure 1. Profil sismique de la Terre
Les études sismiques montre également que le noyau externe, lui, est liquide et dans les conditions de pression auxquels il est soumis, sa température doit être supérieure à 3.800°C. Mais tout ceci est encore bien vague. Même si on connaît les vitesses sismiques du manteau profond, on ne connais pas assez précisément les propriétés des matériaux du manteau en fonction de la pression et de la température, et on a des doutes sur leur nature exacte, si bien qu'il est difficile d'en déduire des températures. Comment aller plus loin ?
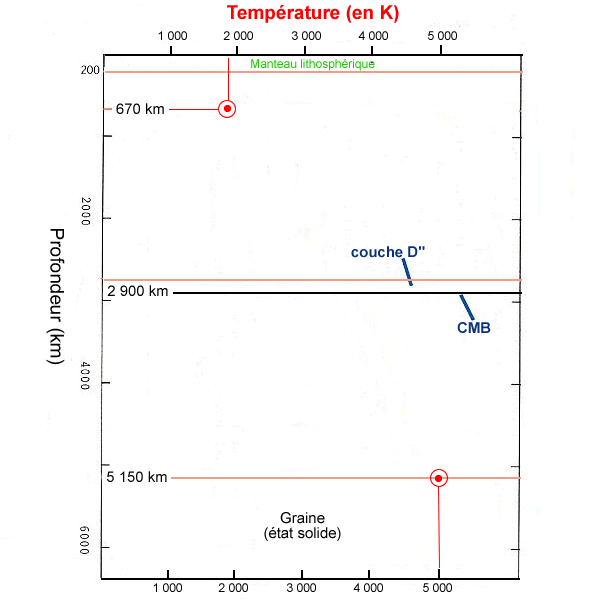
Deux points d'ancrage pour estimer le géotherme
Les scientifiques sont relativement certains des températures en deux points : à 670 km de profondeur (1.600°C), et à 5.150 km de profondeur (limite noyau-graine) (5.000 K). Entre ces deux points d'ancrage du géotherme, il ne peut s'agir que d'estimations.
Une première estimation de gradient à partir des points d'ancrage peut être réalisée. D'après les points d'ancrage, il y a une différence de température de (4.700 - 1.600) soit 3.100°C entre 670 et 5.150 km de profondeur, soit environ 0,7°C par km. Ce gradient de 0,7°C/km est-il cohérent avec ce que nous savons de la Terre ?
Le gradient de température dans une enveloppe qui convecte
La base de l'estimation est la suivante : tellement de chaleur traverse le noyau externe et le manteau inférieur que l'évacuation de la chaleur par conduction ne suffit plus. Des mouvements de matière se mettent en place pour faciliter ce transfert. Ces enveloppes sont tous les deux en régime dit convectif (ceci est indiqué par un nombre de Rayleigh élévé).
Or, les physiciens démontrent que, dans un fluide convectif, les variations de températures ne sont dues qu'à la compression des corps (réchauffement lié à la compression). On parle dans ce cas de gradient de température de type adiabatique. Et un gradient adiabatique, on peut le calculer "facilement".
Figure 3. Expérience simple de visualisation d'une convection
Pour comprendre la notion de gradient adiabatique, voir l'exemple d'un modèle analogique avec fluide en convection.
Extrapoler la température dans le manteau et dans le noyau externe
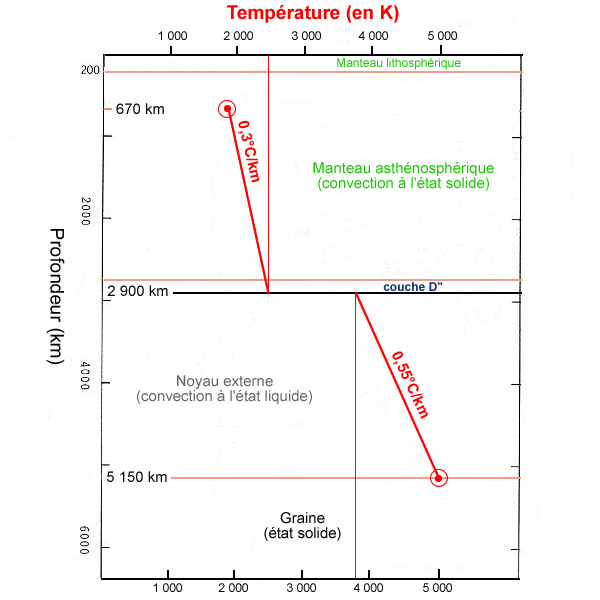
Dans le cas de roches du manteau, on estime le gradient adiabatique à 0,3°C par km. Dans le cas du noyau, il est de l'ordre de 0,55°C par km.
Si on se base sur ces estimations, on peut donc extrapoler la température en tout point du manteau,à partir des points d'ancrage. En remontant depuis 5 150 km (5 000K = 4 700°C) dans le noyau liquide, et en descendant depuis 670 km (1.600°C) dans le manteau, on peut alors estimer la température à la limite manteau-noyau (2.900 km).
On arrive ainsi aux valeurs suivants :
- côté manteau : 1 600 + ( 2 900 - 670 ) x 0,3 soit 2 200 °C
- côté noyau : 4 700 - ( 5 150 - 2 900 ) x 0,55 soit 3 450 °C
Figure 4. Repères et gradients thermiques
Ainsi, le gradient de 0,7°C/km est trop éloigné d'un gradient adiabatique caractéristique de fluides convectifs. Car si on prend ce gradient adiabatique, on arrive à une température de 3 100°C à 2.900 km de profondeur, soit plus de 900°C de différence côté manteau et plus de 300°C de différence côté noyau.
Quoi qu'on fasse, il faut donc affecter plus de 1.200°C à des sauts de température. Envisager des "sauts" de température dans certaines parties du géotherme est une nécessité.
Un saut de température nécessaire
A-t-on des arguments nous permettant de localiser un saut de température ailleurs qu'à la limite noyau-manteau ?
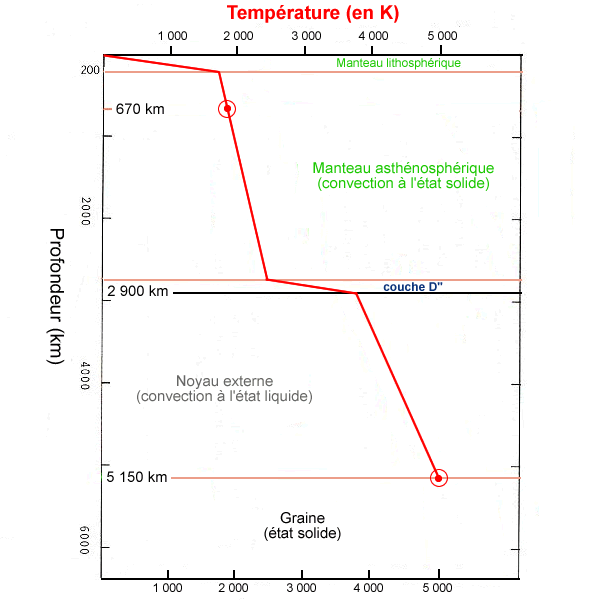
Le seul autre candidat serait la transition des 670 km elle-même. Mais vu les propriétés des deux limites, il semble clair que la limite noyau-manteau (2.900 km) est au moins aussi importante que la limite des 670 km, donc au moins une partie de cet écart de température est, selon toute vraisemblance, absorbé à 2.900 km. Il semble donc difficile d'imaginer une limite noyau-manteau sans saut important de température.
Pédagogiquement, il est plus simple d'affecter la totalité du saut de température à la discontinuité des 2.900 km (discontinuité de Gutenberg). Scientifiquement, il est très probable que le saut ait une ampleur moindre, mais il semble exclu qu'il n'y ait aucun saut de température.
Figure 5. Repères pour tracer le géotherme
Notez enfin que de façon très indirecte, l'importante activité géologique de la couche D" (limite noyau-manteau) plaide plutôt pour un gradient géothermique élevé que pour un calme adiabatique..
Bibliographie
Poirier, J.-P. Les profondeurs de la terre, Masson, Coll. Cahiers des Sciences de l'Univers, 1997. Chapitre 4 pages 76 et suivantes. ISBN-13: 978-2225852237.