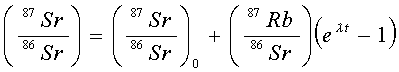Article | 07/07/2002
La géochronologie absolue, cas de la méthode Rb-Sr
07/07/2002
Résumé
Principe de la méthode de datation radiochronologique, application au couple rubidium-strontium. Mesures des rapports isotopiques, notion d'erreur statistique.
Table des matières
Principes généraux
Soit un isotope père P, radioactif, qui se désintègre en un isotope fils F, radiogénique, noté F*.
P → F*
La variation du nombre d'isotopes P est une fonction du temps obéissant à la loi :
dP/ dt = -λP ou encore dP/ P=-λdt
Cette équation s'intègre en fonction du temps en
Ln P = -λt + k
avec k une constante que l'on détermine pour t=0. S'il y a P0 isotopes au temps t = 0 :
P = P0 e-λt
Ainsi, le nombre d'isotopes P diminue en fonction du temps tandis que le nombre d'isotopes fils produit augmente. Pour tout isotope radioactif quelqu'il soit, on définit un temps T appelé période ou demi-vie, au bout duquel il ne reste plus que la moitié des isotopes P présent au départ, autrement dit :
P0 /2 = P0 e-λt ce qui équivaut à λ = Ln 2 / T
On a alors défini λ appelée constante de désintégration de l'isotope radioactif P ; elle équivaut à l'inverse d'un temps et s'exprime en an-1.
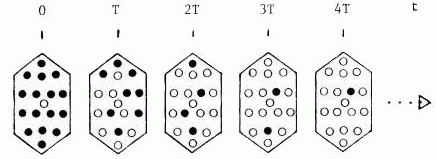
À t = 0, on compte 16 isotopes noirs de P (c'est P0) et 1 isotope blanc de F (F0) :
- À t=T, il ne reste plus que 8 isotopes noirs, 8 isotopes blancs ont été produits.
- À t=2T, il ne reste plus que 4 noirs pour 12 blancs (plus 1 blanc initial),
- À t=3T, il ne reste plus que 2 noirs pour 14 blancs (plus 1 blanc initial),
- etc…
Vous remarquerez que l'on est parti d'un système à 17 isotopes et qu'il y en a toujours 17 dans le système, on dit que le système est clos.
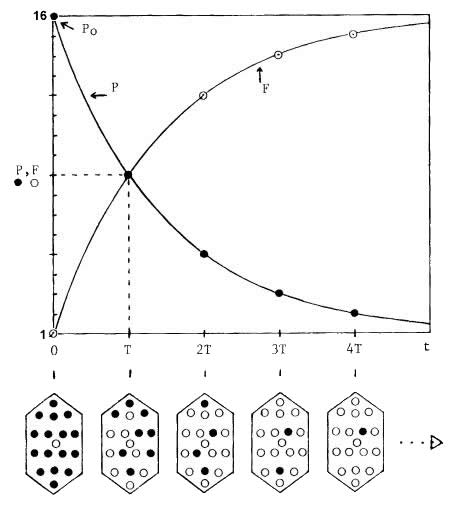
On peut alors dessiner les courbes ci-dessous, avec le nombre d'isotopes P qui diminue en fonction du temps (points noirs) tandis que le nombre d'isotopes fils produit augmente (points blancs).
P → F
Ainsi, pour dater un minéral ou une roche, on peut :
- mesurer le nombre d'isotopes P qui restent dans le système si on connait P0 (comme pour la datation au 14C sur de bois carbonisés) : ce n'est pas très facile car on mesure des quantités de plus en plus faibles d'un atome qui disparaît…
- ou mesurer la quantité d'isotopes F présents dans le système. Dans ce cas, il faut tenir compte du fait que des isotopes F peuvent exister au départ (F0) dans la roche indépendamment de la radioactivité de P.
On a alors F = F0 + F*
Si F* est produit par la désintégration de P, on a F* = P0 - P comme P = P0 e-λt ou P0 = P eλt alors F* = P (eλt - 1).
Il vient immédiatement que F = F0 + P (eλt - 1). (1)
Le cas du couple Rb (rubidium) – Sr (strontium)
87Rb → 87Sr
T = 48,8 Ga, λ = 1,42 10-11 an-1
L'équation (1) devient : 87Sr = 87Sr0 + 87Rb (eλt - 1)
On dispose ici d'une équation à 2 inconnues (87Sr0 et t) et même avec deux échantillons contemporains et cogénétiques, le dilemme ne se résout pas (2 équations à 3 inconnues, t et les deux teneurs initiales en 87Sr) ! Pour résoudre ce problème, il faut comprendre que la cristallisation est un processus géologique qui ne fractionne pas les isotopes d'un même élément lourd. Ainsi, deux minéraux ou deux roches cristallisant à partir d'un même magma intégreront dans leur réseau cristallin du strontium (Sr) avec un rapport isotopique 87Sr/86Sr identique à celui du magma d'origine. On dit que ces échantillons sont cogénétiques. Et même si certains minéraux intégreront plus de strontium que d'autres (suivant la compatibilité de l'élément avec le réseau cristallin en question), tous auront le même rapport initial 87Sr/86Sr.
Par ailleurs, sachant que 86Sr n'est ni radioactif ni radiogénique, la quantité de cet isostope ne varie pas au cours du temps dans un système clos et 86Sr=86Sr0. Si on divise toute l'équation par le nombre d'un autre isotope du Sr, le 86Sr, l'équation devient donc :
Et l'on peut mesurer les rapports 87Sr/86Sr et 87Rb/86Sr par spectrométrie de masse.
Les processus de différentiation des roches magmatiques impliquent des variations des quantités de Rb et de Sr des produits de cette différentiation mais pas du rapport isotopique initial du Sr. Dans ces conditions, 2 échantillons de roches issus du refroidissement d'un même magma auront le même rapport initial (87Sr/86Sr)0 mais des rapports (87Sr/86Sr) et (87Rb/86Sr) différents que l'on peut mesurer. On dispose alors de 2 équations à deux inconnues.
Les schémas ci-dessous récapitulent ce raisonnement en fonction du temps dans un diagramme (87Sr/86Sr) en fonction (87Rb/86Sr) pour 5 ou 6 échantillons d'un même magma de départ (qui ont donc le même rapport (87Sr/86Sr)0).
Si l'on reporte ces deux rapports d'isotopes l'un en fonction de l'autre pour ces 5 ou 6 échantillons, l'équation ci-dessus nous dit que la courbe obtenue sera une droite dont le coefficient directeur (ou pente) donnera le temps écoulé depuis la formation du magma, autrement dit son âge !
À propos de l'incertitude sur les mesures isotopiques et sur les âges obtenus
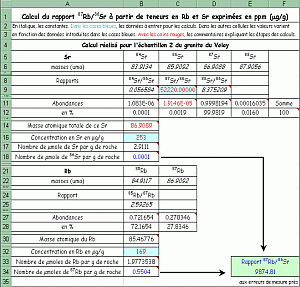
Il faut bien noter que les valeurs des rapports 87Rb/86Sr et 87Sr/86Sr, que les géochimistes mesurent par spectrométrie de masse sont des moyennes de près d'une centaine de rapports mesurés pour chaque échantillon. Elles sont donc affectées d'erreurs statistiques aussi bien en x qu'en y, ce qui donne lors du report sur le diagramme, des rectangles d'incertitude et non pas des points.
La droite "isochrone" passant par ces rectangles d'incertitude doit donc être ajustée au mieux selon des règles mathématiques et statistiques. Les âges obtenus par ces calculs, généralement informatisés, sont donc eux-même affectés d'une erreur de type ±10 Ma, par exemple, et d'un coefficient de confiance ou indice des déviations pondérées (en anglais MSWD ou Mean Standard Weighed Deviation) permettant de contrôler l'alignement des points représentatifs des échantillons (voir par exemple la datation du granite du Velay).
Pour les exemples de datation Rb-Sr donnés ici, nous n'avons pas toujours précisé les erreurs sur les mesures pour ne pas compliquer le report des données. Mais soyez vigilant sur le tracé de la droite isochrone qui passe au mieux à travers les points analytiques : vous pourrez trouver, en comparant vos résultats avec ceux de vos collègues, des variations de ±10 Ma !
En utilisant un logiciel de type Excel ou autre tableur, on pourra calculer une « courbe de tendance » qui donne l'équation de la droite de régression passant par ces points, équation à partir de laquelle l'âge pourra être calculé.