Article | 08/02/2013
Un astéroïde, l'astéroïde 2012 DA 14, passe à moins de 28.000 km de la Terre le 15 février 2013
08/02/2013
Résumé
Passage d'un astéroïde géocroiseur à moins du dixième de la distance Terre-Lune, en deçà de l'orbite des satellites géostationnaires.
Table des matières
L'astéroïde 2012 DA 14
Ce vendredi 15 février 2013, vers 19h24 UTC/GMT (20h24 heure légale française), l'astéroïde 2012 DA 14 "frôlera" la Terre (NASA News, NEOP News, NASA FAQ). En effet, il ne sera qu'à environ 27.700 km à l'aplomb du point de coordonnées 6°S-97,5°E, soit au large de Sumatra dans l'océan Indien oriental. Cette distance est à comparer aux 384.000 km nous séparant de la Lune et à l'altitude de révolution des satellites géostationnaire (télécommunication, météo) d'environ 36.000 km. Le passage d'astéroïdes de quelques mètres de diamètre entre la Terre et la Lune est relativement fréquent (~ une fois par an), mais 2012 DA 14 passera "bien plus loin" que l'astéroïde 2011 MD qui passa à seulement 12.000 km le 27 juin 2011.
L'astéroïde 2012 DA 14 a été découvert en février 2012 à l'observatoire astronomique de Majorque (îles Baléares) par une équipe du programme La Sagra Sky Survey. Il mesure environ 45 m de "diamètre" (plus grande dimension) pour une masse estimée à 130.000 tonnes, soit une densité minimale (volume maximal correspondant à une sphère) de l'ordre de 2,7. Cet astéroïde est donc très certainement composé de roche plutôt que de glace (densité voisine de 1) ou de fer (densité de l'ordre de 8).
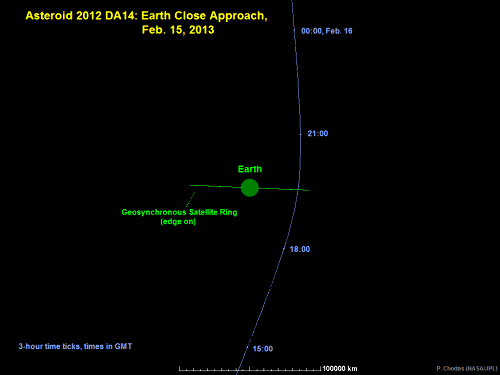
Source - © 2013 NASA / JPL-Caltech Figure 1. Trajectoire de l'astéroïde 2012 DA 14 projetée sur le plan de l'écliptique "Geosynchronous Ring" : orbite géostationnaire. L'astéroïde ne croisera pas la trajectoire de satellites géostationnaires | Source - © 2013 NASA / JPL-Caltech Figure 2. Trajectoire de l'astéroïde 2012 DA 14 perpendiculairement au plan de l'écliptique "Geosynchronous Ring" :orbite géostationnaire. |
Comme on le voit sur le tracé de sa trajectoire, l'astéroïde arrive par le côté Sud de la Terre, en est au plus proche vers l'équateur et continue vers le Nord. L'observation de ce passage n'est pas possible à l'œil nu et demande une grande habileté pour un astronome amateur utilisant jumelles ou télescope car il "défilera" à la vitesse de 1° par minute (soit deux fois le diamètre apparent de la Lune chaque minute). Il faudra être dans l'hémisphère Sud pour observer la phase d'approche et dans l'hémisphère Nord pour la phase d'éloignement. Depuis l'Europe, il faudra être très à l'Est pour espérer observer ce phénomène, qui sera par ailleurs visible d'Afrique, d'Asie et du Pacifique.
Pour suivre les passages proches d'astéroïdes, la NASA propose, sur son site Near Earth Object Program, la liste des prochaines approches (les 3 mois à venir) via le menu Close Approaches.
Géocroiseurs et impacts
Comme à chaque passage d'astéroïde, se pose la question de savoir ce qui se passerait s'il impactait la Terre plutôt que de la frôler.
C'est un astéroïde d'un diamètre estimé à une cinquantaine de mètres, donc proche de 2012 DA 14, qui est à l'origine, il y a 50 ka, du célèbre Meteor Crater en Arizona, astroblème de 1200 à 1400 m de diamètre... Un joli trou ! Cependant, il semble, au vu de l'énergie dégagée, qu'il s'agissait d'une météorite de fer (ou fer-nickel), donc plus dense que 2012 DA 14.
Un autre astéroïde d'un diamètre estimé, lui aussi, à une cinquantaine de mètres, serait à l'origine de la catastrophe de Tungunska (Sibérie) en 1908. En l'absence de cratère, il semble qu'il ait explosé en arrivant dans les basses couches de l'atmosphère, dévastant tout dans un rayon de 20 km, imposant de sérieux dégâts dans un rayon de 100 km et ayant été vu et/ou entendu jusqu'à près de 1.000 km.
Si l'arrivée d'une météorite d'un tel diamètre est estimé se produire tous les 1200 ans, une explosion "classique" en altitude produit généralement l'arrivée au sol de multiples "petits" blocs, comme ce fut le cas en octobre 2008 pour l'astéroïde 2008 TC3 au Soudan (astéroïde découvert seulement une vingtaine d'heures avant son impact car bien plus petit, 2 à 5 m de diamètre initialement).
Petit calcul "simple" et "classique". Si un corps de 130.000 tonnes s'écrasait sur Terre avec une vitesse de 13 km/s, alors l'énergie cinétique libérée (1/2.m.v2) serait de l'ordre de 1,1.1016 J, soit l'équivalent de175 bombes atomiques Little Boy (Hiroshima, 6 août 1945). La vitesse d'arrivée de 13 km/s correspond à la vitesse d'arrivée au sol d'un corps situé à l'infini avec une vitesse initiale de 7 km/s (vitesse relative Terre-2012 DA 14), accéléré en fin de course par l'attraction terrestre (conservation de l'énergie). Si l'attraction terrestre a été prise en compte, cette estimation "à la louche" considère une trajectoire impactant directement la Terre (accélération de même direction que la vitesse initiale) et néglige le ralentissement lié aux frottements sur les basses couches de l'atmosphère, plus difficile à estimer. Rappelons que si on prenait une vitesse plus faible, l'énergie cinétique baisserait "au carré" ; ainsi pour une vitesse d'impact de 6,5 km/s (vitesse divisée par 2), l'énergie cinétique libérée serait alors 4 fois plus faible (~44 Little Boy). Cet effet "protecteur" de l'atmosphère est trompeur car les météorites catastrophiques passées ou futures, sont généralement grosses, denses, "rapides"... et l'effet de frein est alors négligeable.
Conservation de l'énergie mécanique et vitesse de libération
Appliquons le principe de conservation de l'énergie mécanique pour un corps soumis uniquement à l'attraction terrestre.
L'énergie mécanique (Em) est la somme de l'énergie cinétique (Ec) et de l'énergie potentielle (Ep).
L'énergie cinétique est égale à : Ec = 1/2.m.v2 , avec m la masse du corps (kg) et v sa vitesse (m/s).
L'énergie potentielle (liée au champ de pesanteur terrestre) est égale à : Ep = - (G.M.m)/r, avec G la constante de gravitation universelle, M la masse de la Terre, m la masse du corps et r la distance du corps au centre de la Terre.
Pour un astéroïde situé "à l'infini", r est "très grand et l'énergie potentielle initiale est nulle Epinf = 0 ; l'énergie cinétique est égale à Ecinf = 1/2.m.vi2.
Au point "final", lors de l'impact sur Terre, la vitesse est égale à vT et Ep = - (G.M.m)/RT, avec RT le rayon terrestre.
Le principe de conservation de l'énergie mécanique donne donc :
- 1/2.m.vinf2 + 0 = 1/2.m.vT2 - (G.M.m)/RT.
On obtient alors une vitesse finale égale à :
- vT2 = (2GM)/RT + vinf2.
Si on prend une vitesse nulle "à l'infini" (vinf nulle) on retrouve la notion de vitesse de libération, vitesse nécessaire à un corps situé à la surface de la Terre pour quitter l'attraction terrestre (sans vitesse résiduelle), vT = √(2GM/RT), soit environ 11 km/s.