Article | 13/02/2020

Les harmoniques sphériques

13/02/2020

Frédéric Chambat

ENS de Lyon – Laboratoire de Géologie de Lyon

Olivier Dequincey

ENS de Lyon / DGESCO

Résumé

Description unique des fonctions définies sur la sphère par une somme d'harmoniques sphériques, un équivalent des séries de Fourier pour les fonctions définies sur le cercle. Exemple de la reconstruction de la topographie terrestre.

Table des matières

Les harmoniques sphériques, des fonctions mathématiques
Décomposition unique d'une fonction en harmoniques sphériques
Topographie terrestre et harmoniques sphériques

Cet article utilise de nombreuses notations mathématiques (formules et variables dans le texte) écrites en MathML. Certains navigateurs n'interprètent pas correctement ce langage (problème relevé avec Chrome) soit parce qu'ils ne le peuvent pas (rare, voire inexistant), soit parce que l'appel au javascript nécessaire est bloqué (paramètres généraux ou de sécurité du navigateur).

Les harmoniques sphériques, des fonctions mathématiques

Les harmoniques sphériques sont des fonctions mathématiques très utilisées en physique, notamment en mécanique quantique et en géophysique.

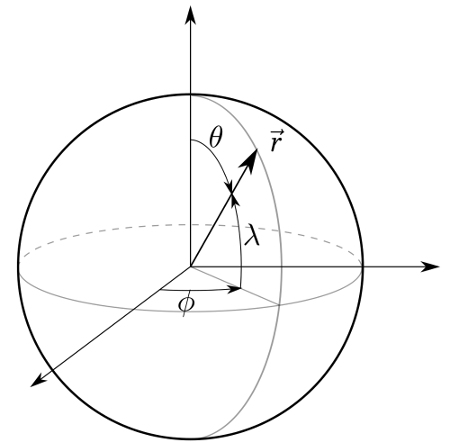
Figure 1. Coordonnées sphériques (rappel)

$r$ ∈ [0, +∞[ est le rayon, $Φ$ ∈ [0, 2π] la longitude, et $θ$ ∈ [0, π] la colatitude ( λ = π/2 − θ est la latitude).

Soient $r$ , $θ$ , $Φ$ les coordonnées sphériques : $r$ est le rayon, $θ$ la colatitude, $Φ$ la longitude. Les harmoniques sphériques, notées $Y_{l}^{m} (θ, Φ)$ , sont des fonctions des deux coordonnées angulaires. L’indice $l$ et l’exposant $m$ sont deux entiers appelés le degré et l’ordre de l’harmonique. Ils prennent les valeurs $l = 0, 1, 2, …, ∞$ , et $m = - l, …, 0, …, l$ .

Les $Y_{l}^{m}$ oscillent en $θ$ et en $Φ$ . Elles s’annulent sur $| m |$ cercles méridiens, et $l - | m |$ parallèles. Une harmonique de degré $l$ a ainsi $l$ lignes de nœuds ( $| m |$ cercles méridiens et $l - | m |$ parallèles). L’échelle spatiale typique de variation d’une harmonique diminue en $1 / l$ , et est commune à toutes les harmoniques d'un même degré $l$ . On appelle cela communément la longueur d’onde, notée $λ_{l}$ . Sur une sphère de rayon $R$ , et pour $l \neq 0$ , elle vaut :

$λ_{l} = \frac{2 πR}{l}$ .

Par exemple, pour représenter une Terre aplatie aux pôles, on utilise $Y_{2}^{0}$ , qui s’annule uniquement sur deux parallèles :

$Y_{2}^{0} (θ) = \frac{3 \cos^{2} (θ) - 1}{2}$ .

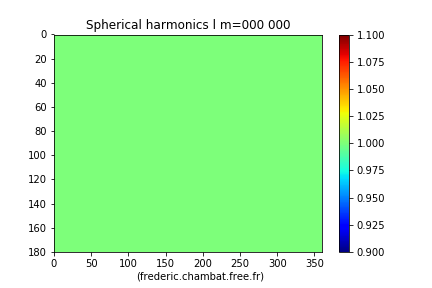
La première harmonique est constante : $Y_{0}^{0} = 1$ .

Les représentations ci-après des harmoniques sphériques sont des projections rectangulaires des latitudes/longitudes, selon une projection cylindrique équidistante. Les valeurs angulaires y sont données en degrés (0 à 180 pour la colatitude, 0 à 360 pour la longitude).

Figure 2. L'harmonique sphérique $Y_{0}^{0}$

Cette harmonique est constante, elle décrit une sphère.

Figure 3. L'harmonique sphérique $Y_{2}^{0}$

Cette harmonique s'annule sur deux parallèles. Elle montre des valeurs positives aux pôles et négatives à l'équateur. Avec un coefficient négatif, on peut l'utiliser pour décrire le déficit de rayon polaire et l'excès de rayon équatorial d'une Terre aplatie aux pôles (et renflée à 'équateur).

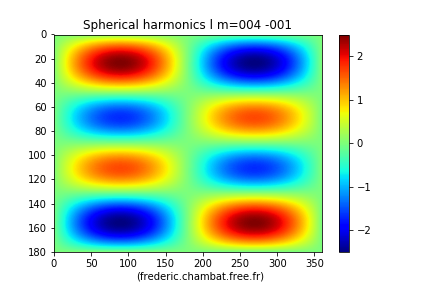
Figure 4. L'harmonique sphérique $Y_{4}^{0}$

Cette harmonique s'annule sur 4 parallèles.

Figure 5. L'harmonique sphérique $Y_{4}^{1}$

Cette harmonique s'annule sur 4 lignes de nœuds, 3 (4−1) parallèles et 1 cercle méridien.

Attention, chaque cercle méridien est représenté par deux lignes verticales (chacune correspondant à un demi-cercle méridien). Ici, les lignes verticales de longitude 90 et 270 (180+90) tracent le même cercle méridien.

Figure 6. L'harmonique sphérique $Y_{4}^{−1}$

Cette harmonique s'annule sur 4 lignes de nœuds, 3 (4−1) parallèles et 1 cercle méridien.

Attention, chaque cercle méridien est représenté par deux lignes verticales (chacune correspondant à un demi-cercle méridien). Ici, les lignes verticales de longitude 0 (= 360) et 180 (180+180) tracent le même cercle méridien.

À degré $l$ égal, les lignes de nœuds méridiennes verticales d'ordre $m$ des harmoniques $Y_{l}^{m}$ et $Y_{l}^{−m}$ sont décalées de 180/2m° [π/2m radians] (ici, avec $m = 1$ , décalage de 90° de longitude).

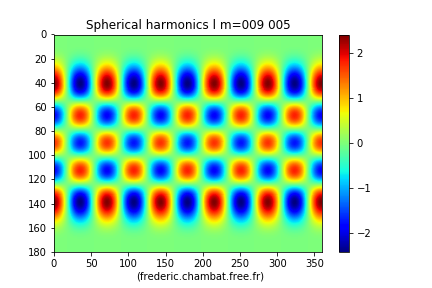
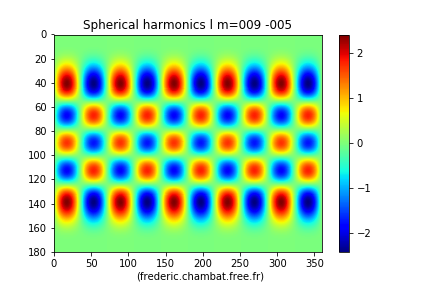
Figure 7. L'harmonique sphérique $Y_{9}^{5}$

Cette harmonique s'annule sur 9 lignes de nœuds, 4 (9−5) parallèles et 5 cercles méridiens.

Figure 8. L'harmonique sphérique $Y_{9}^{−5}$

Cette harmonique s'annule sur 9 lignes de nœuds, 4 (9−5) parallèles et 5 cercles méridiens.

À degré $l$ égal, les lignes de nœuds méridiennes verticales d'ordre $m$ des harmoniques $Y_{l}^{m}$ et $Y_{l}^{−m}$ sont décalées de 180/2m° [π/2m radians] (ici, avec $m = 5$ , décalage de 18° de longitude).

Les harmoniques sphériques de degré 0 à 10 et de tout ordre, ainsi que les harmoniques de degré 30, 100, 600 et 999 jusqu’à l'ordre 10 vous sont proposées (représentations en carte comme ci-dessus) au téléchargement dans le fichier compressé harmoniques-spheriques-Ylm.zip (chaque harmonique $Y_{l}^{m}$ correspond au fichier FC_SHl_m.png). Ces fichiers permettent de visualiser au total 205 harmoniques sphériques et, par exemple, de compléter jusqu'au degré 10 ( $l = 10$ ) une figure qui propose une vue de toutes les fonctions $Y_{l}^{m}$ jusqu'à l'ordre 4, comparable à la figure ci-dessous (qui s’arrête à l’ordre 3).

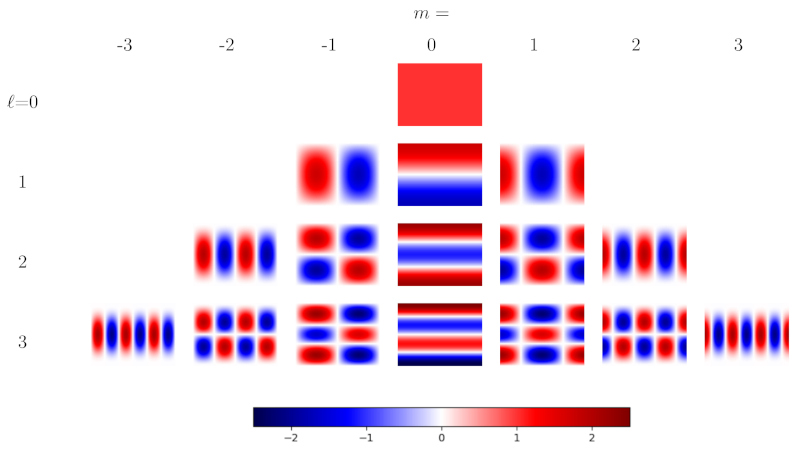
Figure 9. Présentation des harmoniques sphériques $Y_{l}^{m}$ de tout degré $m$ jusqu'à l'ordre $l = 3$

Les harmoniques sont représentées en plan, avec le méridien de longitude nulle à gauche.

Un autre mode de représentation, sur sphère, est aussi proposé.

Figure 10. L'harmonique sphérique $Y_{3}^{2}$ en représentation sur “globe”

Cette harmonique s'annule sur 3 lignes de nœuds, 1 (3−2) parallèle et 2 cercles méridiens. Par rapport à une vue “à plat”, on ne voit que la moitié de la surface de la sphère.

Cette vue nous montre que la sphère est légèrement “penchée” vers nous puisqu'on en voit le “pôle”, croisement des 2 cercles méridiens “nuls” figurés par les traits blancs. Le parallèle qui s'annule (en blanc) est, ici, l'“équateur” de la sphère.

Les harmoniques sphériques individuelles de degré 0 à 5 et de tout ordre sont disponibles au téléchargement dans le fichier compressé harmoniques-spheriques-Ylms.zip (chaque harmonique $Y_{l}^{m}$ correspond au fichier SPl_m.png). Ces fichiers permettent de visualiser les harmoniques individuellement et, par exemple, de compléter jusqu'à l'ordre 5 une figure allant jusqu’à l’ordre 4, comparable à la figure ci-dessous qui s’arrête à l’ordre 3.

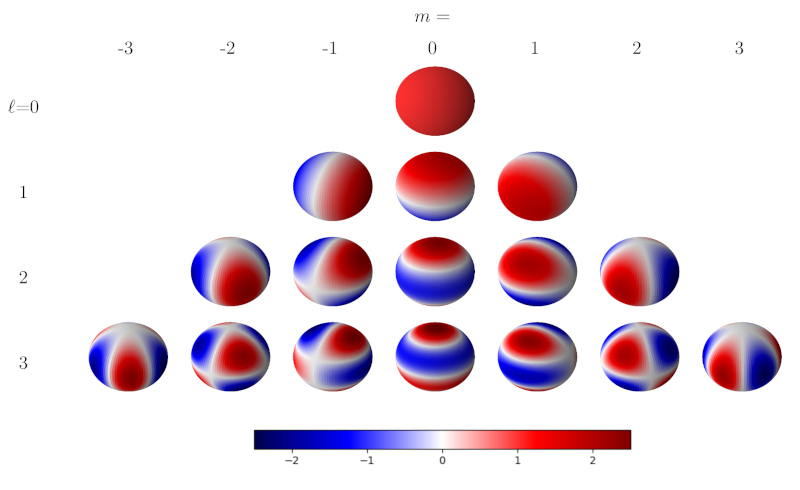
Figure 11. Présentation des harmoniques sphériques $Y_{l}^{m}$ de tout degré $m$ jusqu'à l'ordre $l = 3$

Les harmoniques sont représentées sur une sphère. Le méridien de longitude nulle est à 45° à l’Ouest du méridien orienté vers le lecteur, et est matérialisé, par exemple, sur la ligne $Y_{1}^{−1} = 0$ .

Une version de meilleur résolution des figures 9 et 11 est proposée au téléchargement : harmoniques-spheriques.pdf.

Décomposition unique d'une fonction en harmoniques sphériques

La propriété la plus importante des harmoniques sphériques est que toute fonction définie sur la sphère peut se décomposer de façon unique sous la forme d’une somme d’harmoniques sphériques :

$\forall f (θ, Φ), ∃ ! f_{l}^{m} ∣ f (θ, Φ) = \sum_{l = 0}^{\infty} \sum_{m = - l}^{l} f_{l}^{m} . Y_{l}^{m} (θ, Φ)$ (éq. 1).

Les $Y_{l}^{m}$ forment ainsi une base des fonctions définies sur la sphère. Elles sont l’équivalent, sur la sphère, des séries de Fourier sur le cercle. Les $f_{l}^{m}$ sont les coefficients du développement et peuvent être écrits en fonction de $f$ :

$f_{l}^{m} = \frac{1}{4Π} \int_{0}^{2Π} \int_{0}^{Π} f (θ, Φ) . Y_{l}^{m} (θ, Φ) . \sin (θ) . dθ . dΦ$ (éq. 2).

Ceci permet de représenter une fonction, non par des valeurs en des points [les $f (θ, Φ)$ ], mais par une série de nombres représentant l’amplitude de chaque longueur d’onde [les $f_{l}^{m}$ ].

Topographie terrestre et harmoniques sphériques

La topographie terrestre est un exemple de fonction définie sur une sphére qui peut donc être décomposée en une somme d'harmoniques sphériques.

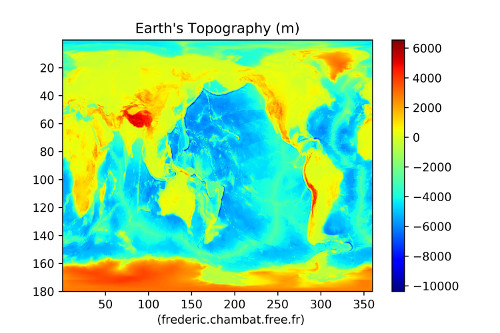
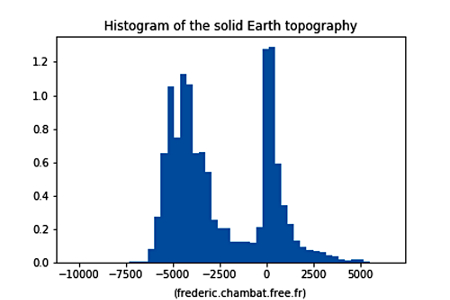
Figure 12. La topographie terrestre

Figure 13. Distribution des altitudes sur Terre

Les valeurs allant au-delà de 6000 m et en deçà de −6000 m sont peu fréquentes.

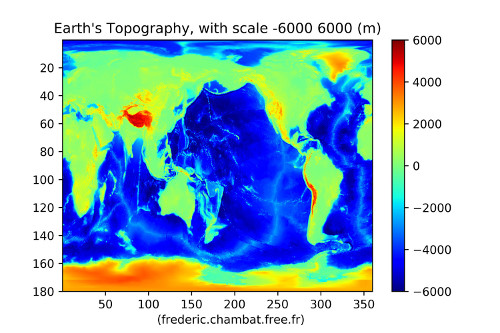
Figure 14. Topographie terrestre avec une échelle d'altitude de −6000 m à +6000 m

La topographie est ici représentée avec une échelle d'altitude limitée à ±6000 m pour faciliter la comparaison avec les cartes de reconstruction en harmoniques sphériques. L'échelle des altitudes utilisant toute la gamme des couleurs, l'altitude “0” passe du jaune-vert au bleu-vert (centre de l'échelle colorimétrique).

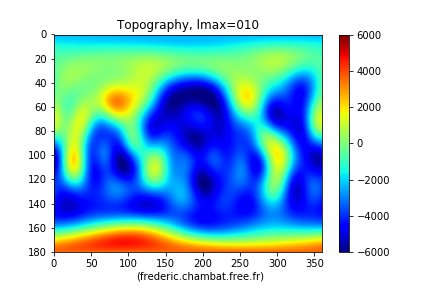
La série de figures suivante est une illustration de développement de la topographie en harmoniques sphériques : la topographie étant connue, on estime les coefficients grâce à la relation éq.2 puis on reconstruit la fonction par la relation éq.1 jusqu’à $l = l_{\max}$ fini. Ces figures montrent cette topographie reconstruite en fonction de $l_{\max}$ .

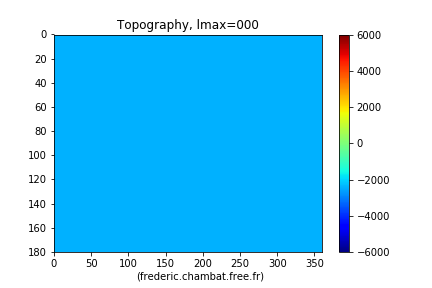
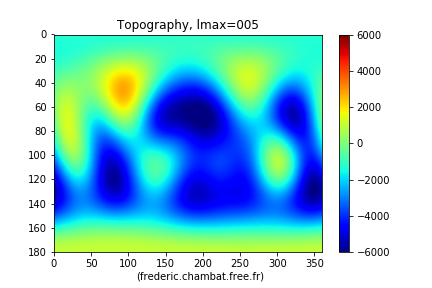
Source - © 2020 Frédéric Chambat Figure 15. Décomposition s'arrêtant au degré 0 Au degré 0, la Terre est à une profondeur moyenne de l'ordre de 2300 m.	Source - © 2020 Frédéric Chambat Figure 16. Décomposition s'arrêtant au degré 5 Au degré 5, on devine les continents.
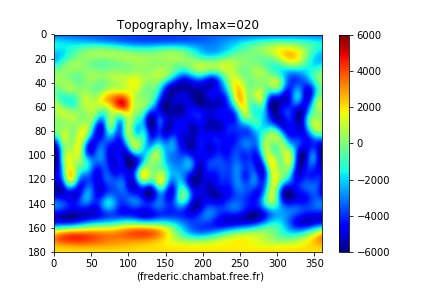
Source - © 2020 Frédéric Chambat Figure 17. Décomposition s'arrêtant au degré 10 Au degré 10, les contours des continents s'affinent.	Source - © 2020 Frédéric Chambat Figure 18. Décomposition s'arrêtant au degré 20 Au degré 20, certains domaines océaniques (fosses, dorsales et iles de taille moyenne) se dessinent.
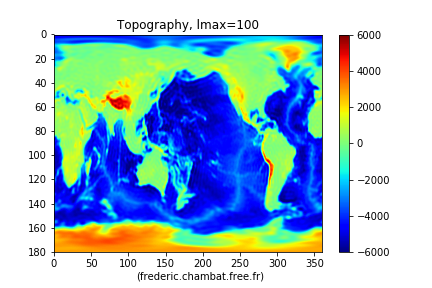
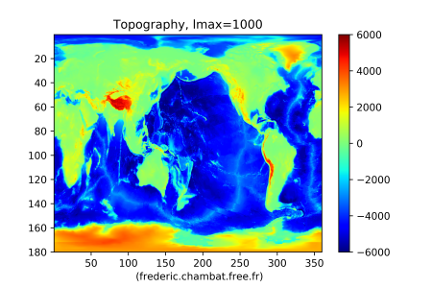
Source - © 2020 Frédéric Chambat Figure 19. Décomposition s'arrêtant au degré 100 Au degré 100, les montagnes se précisent, les dorsales, les iles et les fosses aussi.	Source - © 2020 Frédéric Chambat Figure 20. Décomposition s'arrêtant au degré 1000 Au degré 1000, on retrouve la carte topographique de départ “limitée” à ±6000 m, c'est-à-dire sans les valeurs extrêmes inférieures à −6000 m ou supérieures à +6000 m.

Figure 21. Reconstruction de la topographie terrestre par addition successive d'harmoniques sphériques

Téléchargez le film en webm ou mp4.

Téléchargez le fichier zip des 94 images de l'animation, comprenant la topographie terrestre + les 93 étapes proposées : tous les $l_{\max}$ de 0 à 30, puis 1 sur 5 de 35 à 100, puis 1 sur 10 de 110 à 300, et 1 sur 25 de 325 à 1000 (le numéro final de chaque image correspond au $l_{\max}$ de la somme des harmoniques).

Les harmoniques sphériques sont aussi utilisées pour décrire la forme théorique de la Terre en rotation sur elle-même, voir, par exemple, La Terre aplatie : le théorème de Clairaut.

Outils personnels

Navigation