Article | 21/02/2003
Lavabos, Coriolis et rotation de la Terre
21/02/2003
Résumé
Expériences abordant le sens de rotation de l'eau dans un lavabo dû à l'effet Coriolis.
Objectifs
Est-ce la Terre qui tourne sur elle-même ou le ciel qui tourne autour de la Terre ? Du point de vue mathématique, les deux hypothèses sont strictement équivalentes puisque ce n'est qu'un problème de repère. Et pourtant, les livres nous affirment que le premier énoncé est le bon alors que le second est faux. Mais qu'en sait-on ? Peut-on imaginer une expérience simple qui en donnerait une preuve ?
On cite souvent le pendule de Foucault. C'est réalisable, très démonstratif, mais difficile à expliquer. En effet le plan des oscillations d'un pendule n'est fixe par rapport aux étoiles qu'aux pôles et le problème est complexe à nos latitudes. À Dijon par exemple, ce plan effectue une rotation en plus de 32 heures par rapport au sol, et non en 24 heures.
La déviation de la chute des corps vers l'Est est une autre expérience qui a été réalisée en 1804 dans un puits de mine. On a mesuré une déviation de 11 mm pour une hauteur de chute de 85 m. Pas très facile à mettre en œuvre.
Autre idée souvent avancée : le sens de rotation de l'eau dans un lavabo ou une baignoire qui se vide. Ce serait le sens des aiguilles d'une montre dans l'hémisphère Sud et le sens inverse dans l'hémisphère Nord. C'est ce problème qui m'intéresse ici.
Approche simple de la force de Coriolis
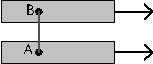
Explications simplifiées sur des tapis roulants
| |
| |
|
Explications simplifiées sur Terre
Dans l'hémisphère Nord. |
|
En conclusion, si vous lancez une balle en suivant le méridien dans l'hémisphère Nord, elle sera déviée vers la droite.
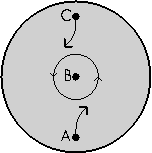
Dans un lavabo |
|
Dans l'hémisphère Sud. |
|
On obtient donc la situation inverse de l'hémisphère Nord : les lavabos de l'hémisphère Sud doivent se vider dans le sens des aiguilles d'une montre.
Un peu de calculs (pour l'hémisphère Nord)
(Dans la suite du texte, les terme en gras dans les formules sont des vecteurs)
Considérons un mobile A se déplaçant sur la Terre avec une vitesse v (dans un repère lié à la surface terrestre). Ce mobile sera soumis à une accélération appelée accélération de Coriolis due au fait que le repère terrestre est en rotation par rapport aux étoiles.
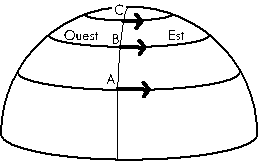
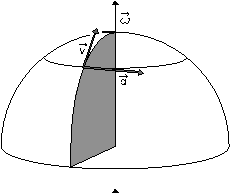
Les formules de changement de repère donnent a = -2ω∧v où v est le vecteur caractérisant la rotation de la Terre (de même direction que l'axe de la Terre, vers le Nord et dont la norme est sa vitesse angulaire). On peut vérifier ce que donne cette formule dans différents cas. Pour plus de clarté, le plan du méridien est représenté en grisé.
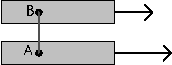
1er cas : lancer vers le Nord. On retrouve la déviation vers l'Est comme dans le lancer de A vers B. | 2ème cas : lancer vers le Sud. On obtient cette fois une déviation vers l'Ouest comme dans le lancer de C vers B. |
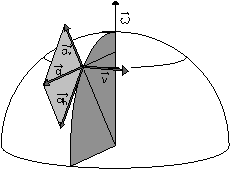
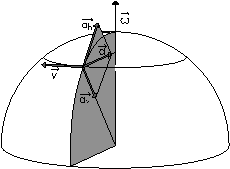
3ème cas : lancer vers l'Est. L'accélération a se décompose en une accélération horizontale ah vers le Sud (c'est toujours une déviation vers la droite) et une accélération verticale av vers le haut. | 4ème cas : lancer vers l'Ouest. L'accélération a se décompose là aussi en une accélération horizontale ah vers le Nord (c'est toujours une déviation vers la droite) et une accélération verticale av vers le bas. |
On obtient donc dans tous les cas une déviation vers la droite... Notre lavabo de l'hémisphère Nord doit donc théoriquement se vider dans le sens inverse des aiguilles d'une montre.
Est-ce que ça marche pour le lavabo en théorie ?
Prenons un grand lavabo circulaire de 45 cm de diamètre à une latitude de 45° Nord et cherchons les différences de vitesse. Le parallèle passant par le centre du lavabo mesure 2πr (r étant le rayon de ce parallèle), soit environ 28.300 km ce qui donne une vitesse linéaire due à la rotation de 1180 km/h.
On peut calculer que celui passant par le bord Sud mesure seulement 1 mètre de plus. La différence de vitesse linéaire entre le bord Sud et le centre du lavabo n'est que de 4 cm/h, ce n'est vraiment pas beaucoup. Il ne semble pas évident que le lavabo puisse s'en apercevoir.
En terme d'accélération, si on considère un courant d'eau se dirigeant du Sud vers le centre à la vitesse d'un piéton pressé (2 m/s ou 7,2 km/h), on obtient une accélération de Coriolis dirigée vers l'Est de 0,0001 m/s², à comparer aux 9,81 m/s² qui attirent l'eau vers le bas. Est-ce que vraiment l'eau de notre lavabo sera affectée par cette légère déviation ? La meilleure solution pour le savoir est de faire l'expérience.
Dispositif
Si vous videz votre lavabo sans précautions particulières, il risque de se vider dans n'importe quel sens, parfois dans le sens direct, parfois dans le sens des aiguilles d'une montre. L'eau n'est jamais au repos et le léger mouvement initial induira le sens de rotation.
Pour essayer de faire l'expérience plus sérieusement, il faudra donc laisser reposer l'eau suffisamment longtemps pour qu'elle soit quasiment immobile. Il faut compter au moins 1 heure. Pour bien voir l'écoulement de l'eau, je conseille de saupoudrer au départ un peu de poivre moulu à sa surface. Malheureusement, pour que l'eau s'écoule, il faut ouvrir la bonde et on amène ainsi un mouvement non contrôlé. De plus, il faut aussi tenir compte de la forme même du lavabo. Les conditions d'expérimentation me paraissent alors mauvaises. En réalité dans mes essais, l'écoulement m'a toujours paru radial, sans rotation, quand je laisse reposer suffisamment longtemps. L'expérience est peut être plus concluante avec une baignoire qui permet des vitesses plus importantes.
Pour éviter le problème de la bonde, j'ai réalisé le montage suivant. Prenez un saladier en plastique, le plus grand possible. Percer le bien au centre en prévoyant le trou de la taille d'un bouchon de stylo feutre. Polissez ensuite pour enlever les aspérités. Obturez le trou avec le bouchon. Installez votre bassine sur deux tasseaux en bois au-dessus du lavabo par exemple, Remplissez d'eau, saupoudrez d'un peu de poivre et laissez reposer. Après une heure ou plus, enlevez délicatement par en dessous le bouchon et notez le sens de rotation de l'eau.
Résultats
Mon 1er essai, avec une bassine de 21 cm de diamètre
Figure 1. Avec un premier saladier de 21 cm de diamètre
Ici, l'eau n'était pas totalement immobile au départ !
L'eau s'écoule ici en tourbillonnant dans le sens des aiguilles du montre, contrairement à ce que nous enseigne Coriolis pour l'hémisphère Nord. Tout cela parce qu'elle n'était pas totalement immobile au départ et possédait déjà un léger mouvement de rotation dans le sens indirect, qui s'est amplifié quand la bassine s'est vidée.
Figure 2. Si l'eau a suffisamment reposé...
Si l'eau a suffisamment reposé, l'écoulement (visualisé ici par une goutte d'encre) est presque totalement radial comme on le voit sur cette photo. Ce n'est que peu avant la fin, qu'un léger mouvement de rotation dans le sens direct s'observe à la surface. Quelques particules de poivre flottant sur l'eau permettent de s'en apercevoir. J'ai obtenu, sur 10 essais, 9 sens inverses des aiguilles d'une montre (sens direct) et un écoulement radial, sans rotation visible.
Mon 2ème essai, avec une bassine plus grande, de 34 cm de diamètre, et un plus grand trou
Avec une bassine plus grande, de 34 cm de diamètre et un plus grand trou pour que la vitesse de l'eau soit plus importante, je pensais que l'expérience serait au moins aussi concluante. Or, j'ai trouvé dans tous les cas un écoulement parfaitement radial.
Mon 3ème essai, avec une bassine un peu plus petite, de 28 cm de diamètre, et un trou de 8 mm
Les résultats semblent plus concluants : encore 9 sens de rotation directe sur 10 et un sans rotation visible. L'écoulement semble pourtant radial au début. Une goutte d'encre lâchée délicatement dans l'eau montre bien ces mouvements. Et ce n'est qu'un peu avant la fin que l'on voit les particules de poivre à la surface démarrer une rotation indirecte. Elle est parfois nette, parfois juste amorcée.
Il faut d'ailleurs éviter de mettre trop de poivre sinon les particules s'agglomèrent et la rotation est moins visible. Il serait intéressant de passer ensuite à la dimension supérieure. Une bassine parfaitement polie d'un ou deux mètres de diamètre pourrait être intéressante. Si l'un d'entre vous a envie d'essayer.
Conclusion
Avec des conditions d'expérimentation précises, on peut penser qu'il est possible de trouver ainsi une preuve physique de la rotation de la Terre sur elle-même. Pour pouvoir conclure avec plus d'assurance, il faudrait recommencer l'expérience avec d'autres saladiers, mais les miens sont maintenant tous percés... Et c'est peut-être un léger défaut de mes récipients qui crée le sens de rotation. La meilleure démonstration serait de partir dans l'hémisphère Sud avec ce même saladier pour vérifier que l'eau s'écoule dans l'autre sens. Il n'y aurait alors plus de doutes.
Avis à nos amis de La Réunion.
D'après un article paru dans les Cahiers Clairaut N° 88 de décembre 1999, bulletin du Comité de Liaison Enseignants Astronomes.