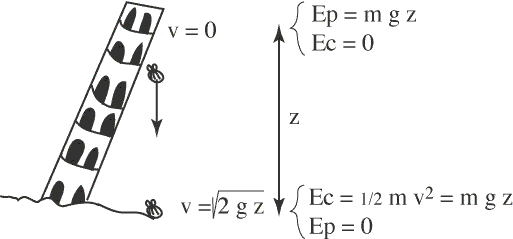Article | 12/03/2001
Mesurer le géoïde en milieu continental
12/03/2001
Résumé
Définition du géoïde, mesure en milieu continental.
Table des matières
(Voir également Comment déterminer le géoide au-dessus des continents ? )
La gravité terrestre
Lorsqu'on lâche un objet de la fenêtre du deuxième étage d'un immeuble, celui-ci tombe vers le sol sous l'effet de la gravité. La gravité terrestre est une force d'attraction, créée par la masse même de la Terre et qui agit à distance, comme l'attraction d'un aimant. Pour obtenir la valeur de la force de gravité, on peut mesurer la vitesse de chute d'objets de différentes masses, comme le fit Galilée depuis la tour de Pise. On obtient alors que les objets ne tombent pas à une vitesse constante mais accélèrent de façon constante. On note g la valeur de cette accélération, dite accélération de la pesanteur. Sur la Terre, la valeur moyenne de g est de 9,81 m/s2.
En physique, il y a une correspondance entre force et accélération. Les pilotes de chasse par exemple sont écrasés sur leur siège au décollage, car l'avion accélère, ce qui crée une force, alors qu'ils ne sont plus écrasés lorsque leur vitesse de vol est atteinte, aussi grande soit elle. L'équivalence entre force et accélération a été formalisée par Newton dans sa seconde loi, qui énonce que la somme des forces f auxquelles est soumis un corps est égale au produit de sa masse m par son accélération a : f = m a. Dans le cas d'un corps qui tombe (en négligeant le frottement de l'air) on obtient f = m g : le corps est soumis à une force égale au produit de sa masse par l'accélération de la gravité ; cette force est la force de pesanteur terrestre.
Sur la Terre, on mesure la force de gravité en utilisant un gravimètre. Cet appareil de mesure est formé d'une masse attachée à un ressort. L'allongement du ressort est proportionnel à la force de gravité exercée sur la masse. En divisant la force mesurée par la masse, on obtient l'accélération de la pesanteur. Sur Terre cette valeur n'est pas constante, mais varie en fonction de l'endroit où l'on fait la mesure. Ce sont ces variations que l'on utilise pour définir la forme de la Terre.
Qu'est-ce que le géoïde ?
Pour définir la forme de la Terre il nous faut en premier lieu définir la notion de potentiel gravitaire. Pour cela, reprenons l'expérience du corps lâché depuis la tour de Pise.
Si on lâche le même objet depuis un étage différent, on obtient que la vitesse de l'objet, mesurée lorsqu'il touche le sol, ne dépend que de g et de la hauteur z de l'étage :
v = √(2gz)
En effet, lorsqu'on lâche l'objet, celui-ci a une vitesse et donc une énergie cinétique nulle. Pendant sa chute, il gagne de l'énergie cinétique. On peut calculer l'énergie cinétique EC du corps à cette vitesse, en utilisant la formule bien connue EC = 1/2.m.v2.
Cependant, comme rien ne se perd, rien ne se crée, mais tout se transforme, l'énergie cinétique EC n'a donc pas été créée, mais a été transformée depuis une autre forme d'énergie. Cette forme d'énergie est l'énergie potentielle de gravité EP, qui, pour un corps a une altitude z, vaut donc m.g.z.
En écrivant la conservation de l'énergie, on obtient EC = EP = m.g.z d'où v = √(2gz).
Toutefois, il faut souligner que la surface de la mer varie en permanence sous les effets conjugués des marées, des vents et de la pression atmosphérique. Aussi, est-il toujours nécessaire de préciser l'intervalle de temps sur lequel on considère la moyenne.
m.g.z est donc la quantité d'énergie transformée sous forme cinétique lorsque l'objet atteint le sol. Dans un barrage, c'est la libération de l'énergie potentielle de gravité de l'eau stockée qui est transformée en énergie électrique par les turbines.
Nous avons donc vu que la force de gravité qui agit sur un corps à une altitude z est f = m.g, et qu'elle correspond à une énergie potentielle EP = m.g.z. La force f est associée à une accélération g, obtenue en divisant f par la masse du corps. De même, on associe l'énergie potentielle à une grandeur U, appelée potentiel de gravité, obtenu en divisant l'énergie de gravité par la masse de l'objet : U = g.z.
L'intérêt de ce potentiel est qu'il ne dépend pas de la masse considérée, mais définit un « champ » en tout point de l'espace, qu'un objet soit présent ou pas. L'énergie potentielle apparaît alors comme la manifestation du potentiel de gravité lorsqu'une masse est placée dans le champ.
On peut comprendre cette notion à partir de l'exemple du champ magnétique créé par un aimant. Ce dernier est toujours présent, mais on ne voit ses effets que lorsque l'on place un bout de métal dans le champ créé par l'aimant.
Il existe une relation particulière entre le potentiel de gravité g.z et l'accélération de la gravité g : la gravité est en effet la dérivée du potentiel (on vérifie facilement dU/dz = d(gz)/dz = g). Autrement dit, si le potentiel de gravité était une droite, l'accélération de la gravité en serait la pente.
Dans le cas de la Terre, le potentiel de gravité U a une valeur constante sur des surfaces, à peu près ellipsoïdales, dites équipotentielles, qui sont perpendiculaires à la direction de l'accélération de la pesanteur (c'est une relation générale entre une fonction dans l'espace et sa dérivée). Comme la gravité marque la verticale (la direction du fil à plomb), les surfaces équipotentielles marquent donc l'horizontal.
En géophysique, on choisit une équipotentielle de référence pour caractériser la forme de la Terre, le GÉOÏDE. On a dit que les équipotentielles marquaient l'horizontal, et on utilise cette propriété pour choisir le géoïde. En effet, on peut montrer en physique que l'interface entre deux fluides, par exemple de l'eau et de l'air, est une équipotentielle. Un niveau à bulle indique l'horizontal selon ce principe. On dispose sur Terre d'un excellent niveau à bulle : la surface des océans.
On définit donc le géoïde comme la surface moyenne des océans, mesurée par les satellites qui survolent le globe et mesurent leur distance à la surface des océans par ondes RADAR. Cette mesure donne donc la forme du géoïde marin, mais il faut ensuite prolonger ce géoïde en dessus des continents pour obtenir la forme complète de la Terre.
Comment obtenir le géoïde en milieu continental ?
Nous allons tenter de comprendre pratiquement comment nous pouvons évaluer la position du géoïde en milieu continental. Le problème n'est pas simple car le géoïde dépend de la répartition des masses dans la Terre, laquelle n'est pas homogène ; il y a des zones froides très denses et des zones chaudes moins denses dans le manteau en convection qui influencent le géoïde.
Pour déterminer le géoïde continental, il faut connaître l'altitude et la localisation du point de mesure ainsi que la valeur et la direction locales de la gravité. Une fois que l'on connaît la gravité et l'altitude, on peut revenir au potentiel de gravité par une transformation mathématique.
Cela revient plus ou moins à reconstruire une droite dont on connaît la pente (g) en chaque point. Ici le problème est plus complexe car le géoïde est une surface, mais on peut illustrer le calcul mathématique simplement pour un monde à deux dimensions au lieu de trois. Dans ce monde à deux dimensions, les planètes sont des disques...
Considérons le cas d'un monde dont la surface est entièrement recouverte d'eau : le géoïde est un cercle. Si une île apparaît à la suite d'une éruption, il se pose le problème de retrouver le géoïde en dessus de l'île.
On connaît le géoïde au bord de l'île, et l'on peut mesurer la gravité et l'altitude de l'île. L'île forme un triangle qui dévie le fil à plomb. Au bord de l'île, le fil à plomb n'est pas dévié, et plus on se rapproche du sommet du volcan, plus le fil à plomb est dévié vers la montagne. On définit un système d'axes (x,z) en utilisant le géoïde marin. Loin du volcan, le vecteur pesanteur g a une composante uniquement selon z; A proximité du volcan, g a une composante selon x qui marque la déviation
À partir des composantes en x et en z du vecteur gravité, on peut revenir aux variations du potentiel de gravité. En effet, mathématiquement, la composante en z de la gravité (gz) donne la variation du potentiel selon z et la composante en x de la gravité (gx) donne la variation du potentiel selon x (gz = dU/dz et gx = dU/dx).
On se place maintenant sur le géoïde au bord de l'île, aux coordonnées x0=0 et z0=0. En un point de mesure sur l'île, situé à une distance x1 du rivage, le potentiel se trouve à une altitude z1 que l'on ne connaît pas. On sait par contre que ce point est sur une équipotentielle qui vaut U0. On connaît la distance x1-x0 et l'on obtient alors la variation de hauteur du géoïde, z1 = z0 - gx/gz (x1-x0). On obtient donc que là où le pendule n'est pas dévié (gx = 0), le géoïde est à la même altitude qu'en dessus des océans. Par contre, dès que le pendule est dévié, le géoïde s'élève proportionnellement.
On remarque que l'on obtient bien que le géoïde est perpendiculaire au vecteur gravité. Pour la Terre, c'est ce même type de calcul qui est utilisé pour prolonger le géoïde marin sous les continents.