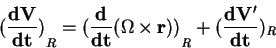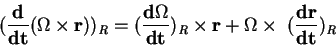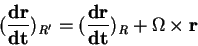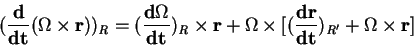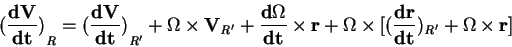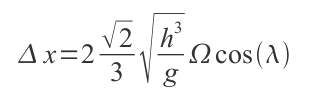Article | 06/02/2002
La mystérieuse "force de Coriolis"
06/06/2002
Résumé
Définition et expression de l'effet Coriolis. Manifestations, mouvement des masses d'air, mythes et mise en évidence.
Table des matières
- Introduction
- Premier contact avec la force de Coriolis
- Expression mathématique de la force de Coriolis
- Quelques manifestations de la Force de Coriolis sur Terre
- Mouvements des masses d'air
- Quelques petits détails en plus
- Expérience permettant de mettre en évidence la force de Coriolis
- Conclusion
- Bibliographie
C'est à cause de la force de Coriolis que les lavabos se vident dans le sens des aiguilles d'une montre dans l'hémisphère Sud, dans le sens trigonométrique dans l'hémisphère Nord, et, comme chacun peut le constater, ne se vident pas à l'équateur.
Cet article a été réalisé dans le cadre d'un projet bibliographique encadré par Gérard Vidal.
Introduction
Pourquoi les nuages s'enroulent-ils toujours dans le même sens autour des cyclones ? Les lavabos se vident-ils dans des sens opposés dans l'hémisphère Nord et dans l'hémisphère Sud ? Et à l'équateur ? Le nom de « force de Coriolis » est généralement associé à ces problèmes, mais les mécanismes détaillés de ces phénomènes restent la plupart du temps méconnus. Le but de cet article est de permettre de compléter les connaissances de chacun sur cette curiosité de la mécanique. Nous avons essayé d'introduire les concepts de façon suffisamment progressive pour que la force de Coriolis soit compréhensible avec un minimum de connaissances préalables.
Premier contact avec la force de Coriolis
Dans cette partie destinée à ceux pour qui la mécanique n'est qu'un lointain souvenir, nous présentons une approche intuitive des forces d'inertie et de la force de Coriolis. Après quelques rappels de mécanique, nous montrons par une expérience simple l'existence de ces forces.
Avant de nous lancer dans le calcul et les applications de la force de Coriolis, nous allons tenter de faire comprendre intuitivement ce qu'elle représente. Il est en effet important en physique de sentir le plus simplement possible la nature profonde du phénomène étudié. Pour cela, quelques rappels de mécanique s'imposent.
Le référentiel
Lorsqu'on étudie un mouvement, il faut définir des positions et des vitesses. Pour cela, il faut savoir par rapport à quoi on définit ces grandeurs. Par exemple, une personne qui se promène dans le sens de la marche dans un train lancé à 150 km/h a une vitesse de 5 km/h par rapport au train, mais de 155 km/h par rapport au sol. Compte-tenu du mouvement de la Terre autour du Soleil, sa vitesse sera aussi 30 km/s par rapport au Soleil, etc. Toute étude de mouvement commence donc par le choix du référentiel. Un référentiel est un solide muni d'un repère, c'est-à-dire un point origine et 3 axes permettant de repérer tout point. Pour le problème du train, un référentiel possible est le train, avec comme repère : {le wagon-bar, l'axe du train, un axe horizontal perpendiculaire au train, et la verticale}. Il faut bien insister sur le fait que le choix du référentiel ne changera pas les conclusions physiques (par exemple, si un calcul dans un premier référentiel conduit à prédire une collision entre deux corps demain matin, on obtiendra la même prévision dans tout autre référentiel).
Changer de référentiel ne change pas la nature du problème, mais sert simplement à simplifier celui-ci d'un point de vue mathématique.
Référentiels galiléens et non-galiléens
Considérons un objet ne subissant aucune force physique (c'est-à-dire liée à une interaction physique : électrique, magnétique, frottements...), par exemple un palet sur une patinoire, pour lequel les frottements sont assez faibles pour être négligés. Le bon sens nous dit que l'objet garde une vitesse et une direction constante : il a un mouvement rectiligne uniforme. Ceci constitue le principe d'inertie : si aucune force ne s'applique sur un mobile, il garde un mouvement rectiligne uniforme (ou reste immobile : mais c'est un cas particulier de mouvement rectiligne uniforme). Ceci n'a cependant rien d'évident, et n'est vrai que dans certains référentiels appelés référentiels galiléens : de nombreux référentiels ne sont pas galiléens, comme on va le voir plus loin. Cependant on admet qu'il existe des référentiels galiléens, dans lesquels un point qui n'est soumis à aucune force garde un mouvement rectiligne uniforme. Dans un tel référentiel, la loi de Newton, qui relie force et accélération, s'applique : F = m.a. Si un point de masse m subit de la part de son entourage des forces de somme F, son accélération sera donnée par F divisé par m. Dans le cas F = 0, on retrouve bien a = 0 soit un mouvement rectiligne uniforme.
Une propriété fondamentale des référentiels galiléens est la suivante ; si un référentiel R1 est en mouvement rectiligne uniforme par rapport à un référentiel R2 galiléen, alors il est lui-même galiléen. Comme exemple de référentiel galiléen, on peut citer par exemple le référentiel héliocentrique (le Soleil au centre, et trois axes pointant vers trois étoiles fixes). En effet, une sonde lancée de la Terre vers l'extérieur du système solaire n'est pratiquement soumise à aucune force, et elle continue sa course en ligne droite à vitesse constante.
Mais l'expérience quotidienne nous apprend que de nombreux référentiels ne sont pas galiléens. Lorsqu'une voiture freine brutalement, il est bien connu que ses passagers sont poussés vers l'avant. Dans le référentiel de la voiture, aucune force « physique » ne s'applique à eux, et pourtant, il subissent une accélération vers l'avant. Le référentiel de la voiture qui freine n'est donc pas galiléen. On ne peut plus y appliquer simplement F = m.a. Faut-il pour autant abandonner cette loi ? Non, et c'est là que réside le secret de la force de Coriolis : pour conserver une loi ressemblant à la loi de Newton, les physiciens utilisent une manipulation astucieuse qui consiste à garder la loi de Newton F = m.a à condition d'ajouter aux forces physiques des « pseudo-forces » ou « forces d'inertie » qui se calculent en connaissant les caractéristiques du référentiel. On aura alors m.a = Fphy + Finertie. Dans le cas de la voiture qui freine, on montre que Finertie est proportionnelle à la masse du passager et à l'accélération, mais en sens contraire. Donc, si la voiture freine (accélération vers l'arrière), le passager subit bien une force (d'inertie) vers l'avant (il est projeté sur le pare-brise).
Cas du référentiel tournant
Dans le cas qui nous intéressera plus loin, les référentiels dont nous nous servons sont les référentiels terrestres, définis par un point de la surface de la Terre, et trois directions fixes pour un observateur placé en ce point, par exemple la verticale, l'Est et le Nord. Un tel référentiel est en rotation par rapport au centre de la Terre. Il va donc nous falloir étudier les référentiels en rotation, cas particuliers de référentiels non-galiléens.
Comme tout le monde l'a déjà expérimenté dans une voiture prenant un virage par exemple, on subit dans un référentiel tournant une force qui pousse vers l'extérieur, communément appelée « force centrifuge » : c'est une force d'inertie, due à aucune interaction physique. Elle est l'analogue pour le référentiel tournant de la force d'inertie vue précédemment). Elle explique par exemple pourquoi les planètes tournent autour du Soleil sans « tomber » dessus : pour les planètes (de même pour les satellites naturels ou artificiels qui tournent autour de la Terre), la force centrifuge compense exactement le force de gravitation.
La force de Coriolis
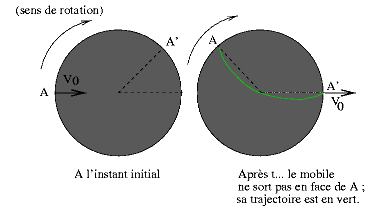
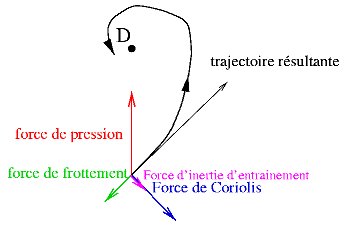
Considérons maintenant un disque horizontal tournant à la vitesse angulaire constante Ω, et un objet (par exemple un glaçon) glissant sans frottement, lancé, à l'instant t=0, du bord du disque vers son centre à une vitesse V0 dans le référentiel du laboratoire (figure 1). Nous allons étudier le mouvement dans le référentiel fixe du laboratoire (galiléen), puis dans le référentiel du disque (non galiléen). Dans le référentiel galiléen, comme il n'y a pas de frottement, le glaçon n'est soumis à aucune force, et donc sa vitesse est uniforme et le glaçon décrit une ligne droite,comme prévu par le principe d'inertie. Mais si notre mobile a laissé une trace d'eau sur le disque, celle-ci n'est clairement pas rectiligne : le point de sortie A' du glaçon n'est pas diamétralement opposé à A .
Figure 1. Mouvement et choix du référentiel
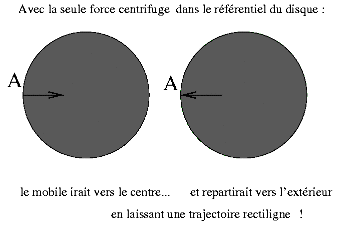
En effet, pendant le temps t que l'objet a mis pour traverser le disque, celui-ci a tourné d'un angle Ω.t. Dans le référentiel du disque, la trajectoire est donc courbe. La force centrifuge ne suffit pas à elle seule à expliquer le phénomène ; s'il avait été soumis à la force centrifuge uniquement,le glaçon aurait été éjecté du disque selon la figure ci-dessous, ce qui n'est manifestement pas la cas vu la forme de la trajectoire.
Il existe donc une autre force d'inertie : c'est la force de Coriolis, du nom d'un ingénieur français du siècle dernier. Quelles en sont les caractéristiques ?
Insistons encore sur le fait que cette force, dite de Coriolis n'est pas une vraie force physique, elle est juste un moyen d'exprimer que les lois de la mécanique changent lorsqu'on change de point de vue. Nous voyons d'abord qu'elle dévie le mouvement vers la gauche dans notre cas (voir figure 1). De plus, il est clair que la force augmente avec Ω (si le disque ne tourne pas, son référentiel se confond avec le référentiel fixe et la trajectoire est une ligne droite). Ensuite, elle dépend de la vitesse du mobile puisque s'il est lancé très vite, la trajectoire est quasiment une ligne droite. Dans la partie suivante nous verrons la forme mathématique de cette force. Mais nous avons ici vu l'essentiel de la physique du problème : la force de Coriolis dévie les objets qui sont en mouvement dans le référentiel terrestre ; c'est une force assez discrète sur Terre car celle-ci a une vitesse de rotation faible devant celle de notre disque !
Ainsi, la force de Coriolis n'est pas une force liée à une interaction physique mais juste une « astuce de calcul » liée au changement de point de vue d'observateur qui exprime, en quelque sorte, que la Terre « bouge sous un projectile » pendant son mouvement. Elle n'est certes pas une « vraie » force, mais il faut néanmoins en tenir compte dès que l'on étudie un mouvement dans un référentiel tournant ! Dans les parties qui vont suivre, nous allons établir sa forme mathématique puis en déduire les effets sur les mouvements de corps sur la Terre.
Expression mathématique de la force de Coriolis
Après la loi de composition des vitesses, nous dérivons de cette relation l'expression de la force de Coriolis.
Rappel de la loi de composition des vitesses
En mécanique, la loi de composition des vitesses qu'on utilise est assez intuitive. Imaginons, comme dans la première partie, le passager d'un train marchant à 5 km/h dans un train roulant à 150 km/h. Une vache regarde passer le train : elle dira que le passager avance à 155 km/h. Exprimons ceci mathématiquement. Considérons deux référentiels R et R', R' se déplaçant à la vitesse U par rapport à R, supposé fixe. Imaginons une particule P se déplaçant à la vitesse V' par rapport à R'. Alors la loi de composition des vitesses donne V la vitesse de P par rapport à R :
V = U + V'
Dans le cas où R' est en rotation par rapport à R autour d'un axe z, à la vitesse angulaire : Ω = Ω.ez
U = Ω x r
V = Ω x r + V'
Expression de la force de Coriolis
On obtient :
Or la dérivation d'un produit vectoriel s'écrit :
et :
D'où on tire :
La formule donnant la composition des accélérations par changement de référentiel est donc finalement :
Il nous reste à présent à interpréter les différents termes de cette formule un peu barbare, afin de voir ce qu'elle signifie physiquement.
Interprétation
Quand on écrit la loi de Newton m.aR' = F + Fe + Fc, on voit apparaître 2 termes en plus de l'accélération de P dans le référentiel R'. On définit la force d'inertie d'entraînement Fie et la force d'inertie de Coriolis Fic.
Fe = -mΩ x (Ω x r)
Fc = 2mVR' x Ω
Dans le cas d'un mouvement circulaire uniforme, la force d'inertie d'entraînement s'écrit Fe = -mΩ2 x ur : on retrouve la force d'inertie vue dans référentiels galiléen et non-galiléen. La force de Coriolis est une force perpendiculaire à la vitesse V. Il ne sera pas possible d'accélérer une particule avec elle, mais juste de dévier sa trajectoire.
Rappel sur le vecteur rotation
Comment caractériser une rotation ? On doit d'abord indiquer l'axe de rotation, ensuite le sens, et enfin la valeur de la vitesse angulaire, par exemple « 500 tours par minute ». Tout ceci peut se résumer en un vecteur, le vecteur rotation . Il s'agit d'un vecteur qui contient toute l'information nécessaire pour caractériser la rotation d'un solide. Sa direction indique l'axe de rotation, son sens est tel que la rotation se fait dans le sens contraire des aiguilles d'une montre quand il pointe vers l'observateur. Sa norme, enfin, est proportionnelle à la vitesse angulaire, mesurée en une unité « naturelle » pour le physicien, le rad/s (6,28 rad/s=un tour/s). Par exemple, la rotation d'une roue de voiture tournant à 10 tours par seconde sera décrite par un vecteur rotation de norme 62,8, horizontal et dirigé vers la gauche de la marche de la voiture.
Rappel sur le produit vectoriel
Étant donné deux vecteurs A et B, on peut construire un troisième vecteur, appelé « produit vectoriel de A et de B ». On l'obtient de la façon suivante. Si dans une base donnée, le vecteur A a pour composantes : (a1,a2,a3), et le vecteur B (b1,b2,b3) , alors le produit vectoriel de A et B s'écrit :
A x B = (a2b3 -a3b2 , a3b1 - a1b3 , a1b2 - a2b1)
D'un point de vue pratique, est un vecteur perpendiculaire à la fois à A et à B. On peut prévoir sa direction par la « règle de la main droite » : si A est représenté par le pouce, B par l'index, alors A x B est donné par la direction du majeur. Ce « truc » sera utile dans la suite pour comprendre dans quelle direction s'exerce la force de Coriolis. Attention à bien prendre la main droite !
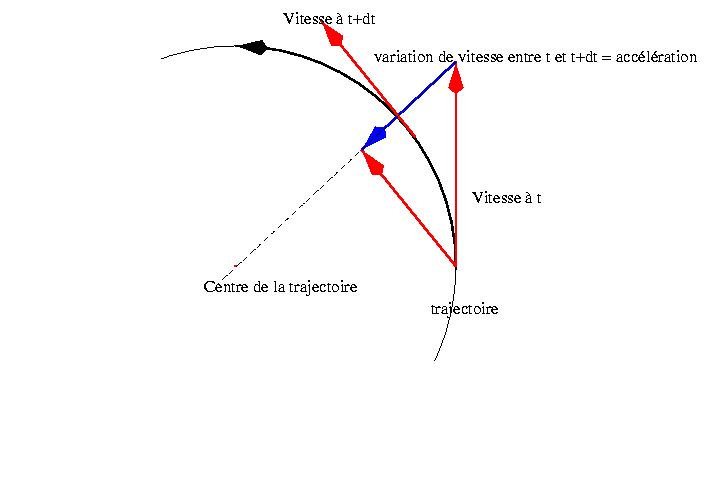
Rappel sur l'accélération
L'accélération est une quantité qui indique les variations de vitesse. Elle s'écrit donc sous la forme : a = dV / dt. C'est une grandeur vectorielle, qui indique comment « bouge » le vecteur vitesse. Mais il ne faut pas croire que parce que la valeur numérique de la vitesse est constante, il n'y a pas d'accélération. Pour bien voir cela, considérons un mouvement circulaire uniforme. Le mot « uniforme » indique que la valeur de la vitesse reste constante. Mais il est clair que sa direction bouge (sinon le mobile irait tout droit). Il y a donc une variation du vecteur vitesse, et donc, une accélération. On peut d'ailleurs trouver la forme de cette accélération, comme le montre le dessin ci-dessous. On voit donc que lors d'un mouvement circulaire uniforme, le mobile est accéléré, et que cette accélération est dirigée vers le centre de la trajectoire.
Quelques manifestations de la Force de Coriolis sur Terre
Maintenant que nous avons établi la forme mathématique de la" force de Coriolis", nous allons voir ses plus célèbres manifestations sur Terre. Dans toute la suite, Ω sera le vecteur rotation de la Terre autour de son axe, orienté du pôle Sud vers le pôle Nord, valant 2π/(24x3600) rad/s (1 tour -2π rad- par jour -24h de 3600s).
Déviation vers l'Est
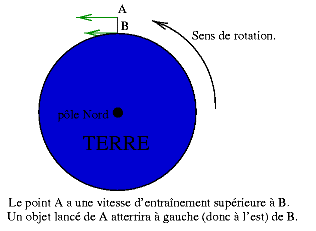
L'expérience de « déviation vers l'Est » concerne la déviation latérale d'un corps en chute libre. On lâche un objet (une bille, par exemple) d'une hauteur h (A) et on observe que l'objet n'atterrit pas exactement à la verticale de là où il a été lâché (B). Le décalage atteint quelques centimètres pour un lâcher du haut de la Tour Eiffel, par exemple.
Figure 4. Chute et déviation
Comment expliquer ceci ? La vitesse de la bille est pratiquement verticale, la force de Coriolis Fc = 2mVR' x Ω est donc dirigée vers l'Est (faire le produit vectoriel par la méthode de la main droite : la vitesse de la bille est selon le pouce, l'axe Nord-Sud de la Terre selon l'index, la "force de Coriolis", selon le majeur, est bien vers l'Est). C'est cette force qui dévie légèrement V vers l'Est. Pour un calcul plus quantitatif, on est confronté à une difficulté mathématique : pour calculer V, on a besoin de connaître l'accélération, donc les forces, mais celle de Coriolis dépend de V... Pour s'en sortir, on procède par une méthode appelée « méthode des perturbations » : on dit que, en première approximation, l'effet de Coriolis est très petit devant la gravitation (environ 100.000 fois plus petit !) et le mouvement est purement vertical : V=gt. Puis de là, on calcule la force de Coriolis résultante et une nouvelle expression de la vitesse corrigée. Et ainsi de suite : nouvelle vitesse, nouvelle force... En pratique, il suffit de calculer la première correction. Cela donne : Fc = 2mVR' x Ω d'où une première expression de la force de Coriolis Fc = 2gt x Ω, puis en intégrant, un vitesse vers l'est qui vaut Vest = gt2 x Ω ; en intégrant de nouveau, on trouve la déviation ∆x = (1/3)t3g x Ω où t est le temps de chute t = √(2h / g). Soit au final, la déviation en fonction de la hauteur :
où λ est la latitude du lieu, 48 degrés pour Paris par exemple. Ceci donne 8 cm pour la Tour Eiffel. Newton avait déjà eu l'intuition qu'un tel phénomène devrait être observé en faisant le raisonnement suivant (voir figure ci-dessus); le point A où la bille est lâchée est plus loin de l'axe de rotation de la Terre et a donc une vitesse plus grande que le point B situé à l'aplomb de A. Il est donc compréhensible que la bille, ayant une vitesse d'entraînement vers l'Est supérieure à celle du point B, atterrisse plus à l'Est que A.
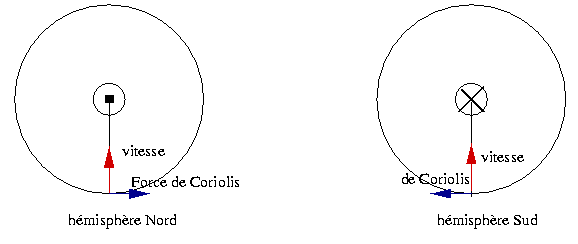
Déviation vers la droite (hémisphère Nord)
Le phénomène de déviation vers la droite (vers la gauche dans l'hémisphère Sud, mais on se placera au Nord dans toute la suite) est sans doute la cause des effets les plus connus dus à la force de Coriolis. Il est notamment à l'origine du sens d'enroulement des nuages autour des anticyclones et dépressions, comme on va le voir plus loin. L'idée de base est simple : pour un objet lancé horizontalement à vitesse constante V, par exemple un obus, la force de Coriolis est perpendiculaire à V et orientée vers la droite vue du l'obus (il suffit de construire le produit vectoriel par la règle de la main droite pour s'en convaincre).
Cet effet est loin d'être négligeable dans certains cas. Car l'accélération résultant de la force de Coriolis vaut Fc = 2mVR' x Ω, soit, en intégrant deux fois, une correction au mouvement rectiligne de l'ordre de VΩt, où t est le temps de vol. Si d est la longueur de la trajectoire, t = d/V et on obtient une déviation vers la droite de l'ordre Ωl2/V. Pour des valeurs de balistique classiques (V=1000 km/h, l=10 km), on trouve quelques dizaines de mètres. Ainsi, pendant la bataille des îles Falkland (hémisphère Sud) durant la Seconde Guerre Mondiale, les canons anglais, réglés pour corriger la force de Coriolis à l'Hémisphère Nord, ont tiré des obus une centaine de mètres à gauche de leur cible ! Sans rentrer dans les détails, le phénomène de déviation vers la droite est aussi à l'origine du fonctionnement du pendule de Foucault (V), de l'usure plus marquée des rails droits sur les lignes droites de chemin de fer, et prend part à la formation des méandres des fleuves. C'est encore lui qui est responsable du sens d'enroulement des nuages autour des dépressions (voir ci-après), et lui toujours qui a créé le mythe tenace du tourbillon dans le lavabo (voir plus loin).
Mouvements des masses d'air
Forces en présence
Avant de commencer l'étude du mouvement des masses d'air, il faut faire le bilan des forces en présence dans le référentiel terrestre pour une quantité d'air de masse m et de volume dV : ces forces sont, en première approximation, au nombre de deux. Ce sont la force de Coriolis et la force de pression.
La force de Coriolis, nous l'avons vu, vaut Fc = 2mVR' x Ω elle courbe la trajectoire vers la droite à l'Hémisphère Nord. Quelle est la forme mathématique des forces de pression ? Même sans savoir exactement ce qu'est la pression, tout le monde a l'intuition qu'une haute pression « pousse » tandis qu'un basse pression « aspire ». Les forces de pression sont donc dirigées des hautes vers les basses pressions. Pour bien comprendre ceci, on peut faire l'analogie suivante : la pression en un point peut être comparée à l'altitude d'un point, et la force de pression serait alors l'analogue de la pesanteur. De même qu'une bille sur un plan incliné subit une force qui la fait descendre selon la ligne de plus grande pente vers les basses altitudes, une masse d'air, de volume dV, descend vers les faibles pressions selon la ligne de plus grande « baisse de pression ». Ceci s'écrit mathématiquement sous la forme F= -dV.grad p, où grad p représente la direction où varie la pression (en quelque sorte une « ligne de pente de pression »).
Anticyclones et dépressions
Comment sont réparties les valeurs de la pression à la surface de la Terre ? La pression de l'air dépend, entre autres, de sa température (l'air froid a une pression plus élevée). Il existe des points (souvent chauds) où la pression est minimale, c'est-à-dire que, tout autour de ce point, la pression est supérieure (un peu comme un trou dans notre analogie avec l'altitude). Un tel point sont appelés dépression. Au contraire, un point où la pression est maximale (une « colline » de pression) est appelé anticyclone.
Mouvement de l'air
De l'anticyclone vers la dépression
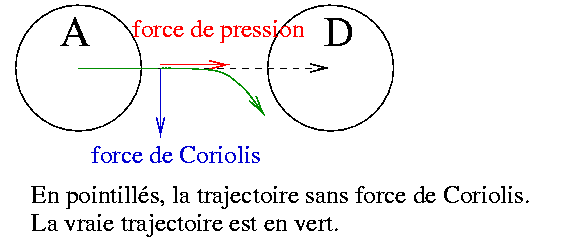
D'après notre analogie pour comprendre la force de pression, l'air, s'il était soumis à cette seule force, « descendrait » en ligne droite de l'anticyclone vers la dépression. Mais dès que l'air est mis en mouvement, il s'y applique une force de Coriolis dirigée vers la droite, ce qui dévie la trajectoire des masses d'air qui ont tendance à contourner la dépression dans le sens contraire des aiguilles d'une montre au lieu de s'y engouffrer directement.
Figure 5. D'un anticyclone vers une dépression
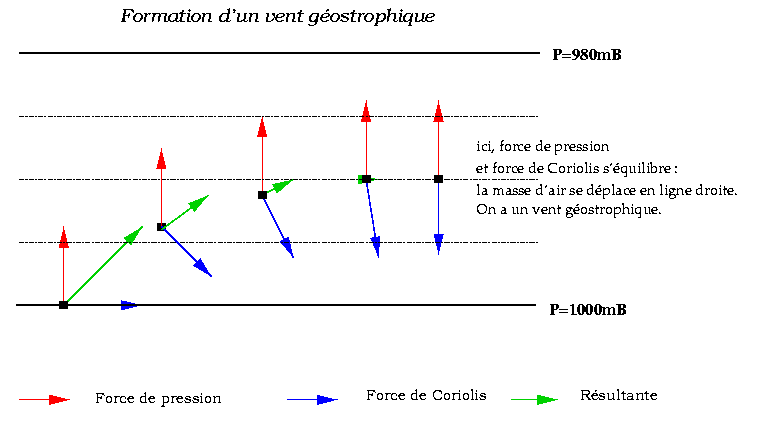
Vent géostrophique
Lorsque la force de Coriolis équilibre la force de pression, le vent n'est soumis à aucune force (au total) et a un mouvement rectiligne uniforme. Un tel vent est dit géostrophique ; on montre alors qu'il suit les lignes de pression constante, appelées isobares.
Figure 6. Vent géostrophique
Mais en réalité, les isobares sont rarement rectilignes, mais plutôt des courbes fermées autour de la dépression. Si de l'air suit une isobare, il s'ajoute alors une force centrifuge (ou « force d'inertie d'entraînement ») due à la rotation de l'air autour du centre. Le bilan des forces montre alors que les masses d'air prennent une trajectoire circulaire dans le sens contraire des aiguilles d'une montre (dans l'hémisphère Nord) autour du centre dépressionnaire.
L'animation ci-dessous montre une dépression dans l'hémisphère Nord. Nous voyons que les trajectoires ont bien le sens prédit (inverse des aiguilles d'une montre), mais ne sont pas circulaires : elles ont une forme de spirale convergeant vers le centre. C'est donc que notre modèle précédent est insuffisant.
Rôle des forces de frictions
Pour obtenir les trajectoires circulaires le long des isobares, nous avons supposé que les masses d'air sont soumises uniquement à la force de Coriolis, à la force centrifuge et aux forces de pression. Mais il existe une quatrième force que nous devons prendre en compte pour une description plus complète : il s'agit des forces de frottement ou de friction. En effet l'air est un fluide légèrement visqueux, ce qui se traduit par une force s'opposant au mouvement au voisinage de la zone de friction avec la terre, donc à basse altitude. Ainsi, à une hauteur inférieure à 1 ou 2 kilomètres, les vents sont ralentis par le contact avec le sol. Cette force est d'autant plus grande que le sol est irrégulier : elle est petite au-dessus des océans mais importante au-dessus des forêts, par exemple.
Figure 7. Enroulement de nuages
Sans les forces de friction, le vent aurait tendance à tourner en cercle autour du centre de dépression, comme on l'a vu plus haut. Mais, en prenant en compte les frottements à la surface de la Terre, les vents de surface sont ralentis et la force de Coriolis, proportionnelle à la vitesse, diminue. La force de pression devient dominante, et ainsi l'air a un mouvement en spirale vers le centre de la dépression.
Figure 8. Impact des forces de friction
De même, les vents s'éloignent du centre pour un anticyclone. Les frottements entraînent donc une convergence des vents vers le centre pour une dépression (respectivement une divergence du centre pour un anticyclone) pour les vents de surface. Comme les masses d'air ne peuvent pas être aspirées par le centre (il faut bien qu'on retrouve cette masse quelque part), elles s'échappent en montant, provoquant des mouvements d'air à l'origine des vents et pluies que l'on retrouve dans la dépression. Pour plus de renseignements sur les cyclones, nous vous proposons d'aller voir la page du Geophysical Fluid Dynamics Laboratory , qui présente de nombreuses images et simulations d'évolutions de cyclones.
Quelques petits détails en plus
Le mythe du lavabo
Nous avons tous entendu un jour cette histoire fabuleuse concernant les lavabos qui se vident. D'après cette histoire, le tourbillon qui se forme au-dessus du siphon tournerait dans le sens des aiguilles d'une montre dans l'hémisphère Sud, dans le sens contraire dans l'hémisphère Nord. Certains chanceux qui ont pu changer d'hémisphère prétendent même avoir pu observer cet effet... L'explication viendrait de la force de Coriolis !
Figure 9. Base physique du mythe du lavabo
En fait on retrouverait le même mécanisme que pour les cyclones. Mais il y a une différence majeure entre les deux phénomènes : leur échelle !
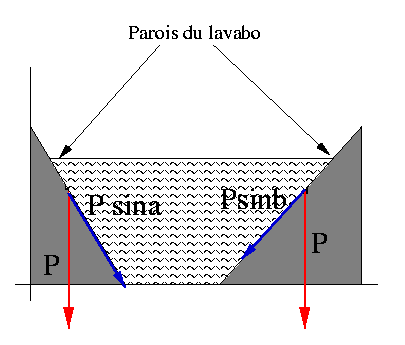
Pour comprendre ce qui se passe dans un lavabo, nous allons essayer de calculer un ordre de grandeur de la force de Coriolis, et la comparer aux autres forces en présences. L'écoulement dans un lavabo a une vitesse faible, de l'ordre de 0,1 m/s. La force de Coriolis par unité de masse a alors, sous nos latitudes, une intensité de l'ordre de Fc = 10-5N.kg-1. Nous allons à présent comparer cette force à celle introduite par une différence de pente entre deux parois du lavabo, comme sur la figure ci-dessous.
Figure 10. Force liée à la forme du lavabo
On considère deux particules de même masse de part et d'autre du siphon. La force qui pousse la particule vers le fond (l'équivalent de la force de pression pour le cyclone) est la projection de son poids sur la paroi. On obtient :
P1 = P x sinα
P2 = P x sinβ
Pour avoir P2-P1 de l'orde de la force de Coriolis, il suffit d'avoir P1-P2= 10-5, soit α - β = 10-6 rad, ce qui correspond pour une baignoire d'un mètre à un écart de µm !!! Autant dire que la moindre irrégularité de surface entraîne une force supérieure à la force de Coriolis, autorisant ainsi le tourbillon à tourner dans le sens qu'il veut (ce sens dépendant essentiellement de ce que l'eau n'est jamais totalement au repos, mais a un sens de rotation privilégié qui sera amplifié par le tourbillon).
Par contre, si on considère un très grand récipient, avec de l'eau initialement bien au repos, alors on peut mettre en évidence l'existence d'un sens de rotation privilégié suivant l'hémisphère. Des physiciens ont réalisés des expériences le démontrant. On pourra par exemple consulter :
- Arsher Shapiro, Bath tub vortex, Nature, 196, 1080-1081, 1962, doi:10.1038/1961080b0, pour l'hémisphère Nord.
- Lloyd Trefeten et al., The bath tube vortex in the southern hemisphere, Nature, 207, 1084-1085, 1965, (doi:10.1038/2071084a0) pour l'hémisphère Sud.
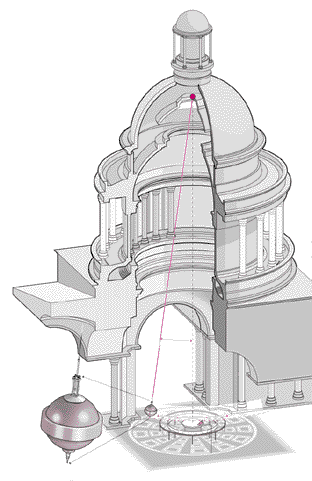
Le pendule de Foucault
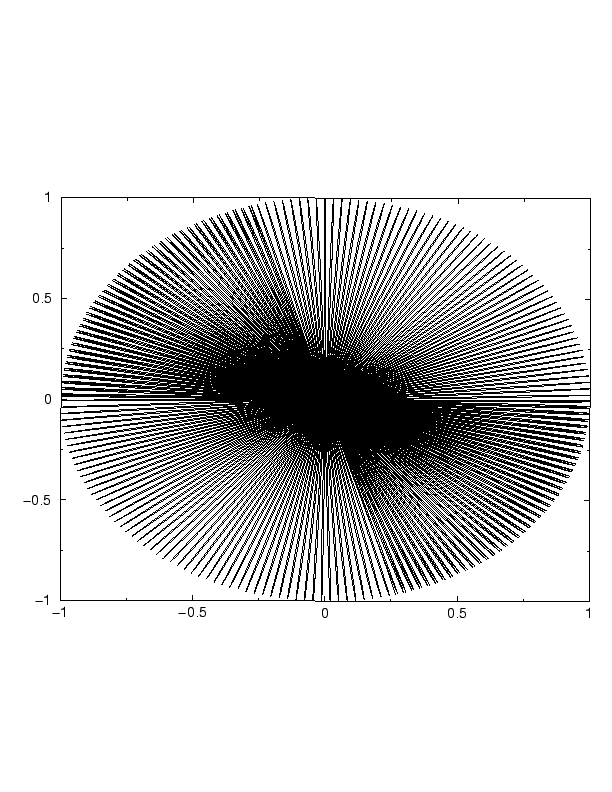
Le pendule de Foucault est l'expérience la plus célèbre sur la force de Coriolis. Elle a été réalisée pour la première fois en janvier 1851 à Paris par Léon Foucault. Il s'agit d'une expérience assez particulière car elle ne démontrait rien de neuf : tous les scientifiques savaient bien que la Terre tournait avant cette date ! Mais jusque-là, les preuves de la rotation de la Terre étaient indirectes, alors que là, il s'agit d'une mise en évidence directe, et qui plus est très visuelle, de cette rotation. C'est la raison pour laquelle cette expérience fut un grand succès populaire : elle fut montée dès le mois de mars 1851 sous la coupole du Panthéon à Paris. La manifestation a été annoncée à la une des journaux. Pour plus de détails sur l'histoire du pendule de Foucault, on pourra consulter le site du Conservatoire National des Arts et Métiers. Le principe de l'expérience est assez simple. On construit un pendule à l'aide d'une grande corde, à laquelle on accroche une masse. Cette masse est munie d'une pointe qui permet de visualiser sa trajectoire dans du sable. Si le référentiel était galiléen, le pendule dessinerait un segment de droite sur le sable. En faisant l'expérience pendant un long moment, Foucault n'as pas obtenu ce résultat, mais une forme plus compliquée, comme celle ci-dessous.
Tout se passe comme si le pendule était, pendant chacune de ses oscillations, dévié vers la droite. Ceci est bien la manifestation qu'une force de Coriolis agit, montrant que le référentiel terrestre n'est pas galiléen. On inclut donc, dans le bilan des forces, la force de Coriolis. Moyennant quelques approximations et quelques calculs, on peut trouver l'équation du mouvement, et la période de rotation de l'axe d'oscillation du pendule de Foucault T = (1/sinλ).TTerre, où λ est la latitude du lieu où est fixé le pendule. L'axe d'oscillation du pendule de Foucault a donc une période de rotation de 24h aux pôles (λ=90°) et une période de rotation "infinie" à l'équateur ((λ=0°).
Lien entre moment cinétique et force de Coriolis
En physique, il est courant d'étudier les objets en rotation depuis un référentiel fixe. Par exemple, si on étudie le mouvement d'une patineuse qui tourne sur elle-même depuis un gradin des tribunes, il est plus logique de se placer dans un référentiel terrestre supposé galiléen. Pour ce genre d'étude, on introduit une quantité vectorielle, le moment cinétique, qui est une sorte de « quantité de rotation » (il est proportionnel au vecteur rotation). Si on munit le référentiel d'un repère dont l'origine est le point O et qu'on considère un point M de l'espace ayant une masse m et une vitesse V, alors on définit le moment cinétique en M par rapport à O par σ = OM x mV. Une propriété importante du moment cinétique est qu'il se conserve en l'absence de force extérieure au système. Il existe aussi une loi donnant l'évolution du moment cinétique si le système est soumis à des forces extérieures (c'est l'analogue de la loi de Newton déjà vue en I). Cet outil est bien adapté pour décrire d'un point de vue extérieur le solide en rotation. Il est intéressant de voir qu'on retrouve les mêmes résultats par le théorème du moment cinétique dans un référentiel galiléen, et par la force de Coriolis dans le référentiel tournant associé.
Nous allons par exemple essayer de recalculer la déviation vers l'Est (bille en chute libre) vue plus haut utilisant le moment cinétique. Un objet de masse m est lâché depuis un point P de l'hémisphère Nord à la latitude λ : initialement, l'objet est au repos par rapport à la Terre en rotation. Sa vitesse angulaire est donc ω.
En posant r + ∆r sa distance au centre de la Terre, on trouve que son moment cinétique vaut m(r +∆r)2.cos2λω. A l'instant t, l'objet est à la distance r du centre de la Terre et a pour vitesse angulaire ω' : son moment cinétique est mr2.cosλω'.
Par conservation du moment cinétique, on trouve m(r +∆r)2.cos2λω = mr2.cosλω' soit : ω' = (1 + ∆r/r)2ω > ω.
En supposant la vitesse de rotation inchangée, on trouve alors que l'objet se déplace vers l'Est à latitude constante avec une vitesse angulaire ω' - ω ≃ 2∆rω/r.
Si on note s la position du point le long du parallèle, on trouve : ds/dt = (ω' - ω)rcosλ = 2∆rωcosλ. Ici, ∆r = 1/2.gt2 est dû à la seule pesanteur. On trouve alors ds/dt = ωgcosλt2 et donc S=1/3ωgcosλt3, ce qui correspond au résultat vu plus haut.
On voit donc que les deux façons de traiter le problème donnent des résultats équivalents (heureusement !). Par contre, l'une des deux méthodes peut être beaucoup plus rapide que l'autre pour trouver le résultat. Un très bon exemple en est l'étude de l'accélération de la rotation d'une patineuse ramenant ses bras le long du corps : la méthode de la conservation du moment cinétique prend au plus cinq lignes, alors que l'étude dans le référentiel tournant est laborieuse. Moralité : le choix du référentiel est fondamental.
Expérience permettant de mettre en évidence la force de Coriolis
Idée de l'expérience
La force de Coriolis croît avec la vitesse de rotation : un moyen simple de rendre ces effets plus importants est donc de faire une expérience sur un plateau tournant assez vite. Il faut ensuite trouver un moyen de tracer la trajectoire du point dans ce référentiel.
Matériel
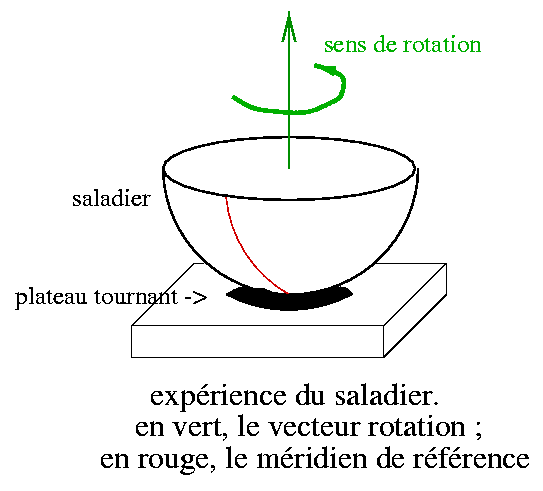
Le montage que nous vous proposons utilise un tour de potier pour enfant, sur lequel on fixe solidement un saladier à peu près sphérique. Le mobile sera un bille, enduite de miel, qui servira de traceur pour suivre la trajectoire dans le référentiel tournant du saladier. On matérialisera sur le saladier un méridien, qui servira de référence pour voir la déviation. Voici donc la liste du matériel:
- Un tour de potier
- Un saladier hémisphérique
- Un pot de miel
- Une bille
- Un feutre indélébile
La figure ci-dessous décrit le montage utilisé.
Figure 13. Montage pour visualiser la force de Coriolis
Interprétation sommaire
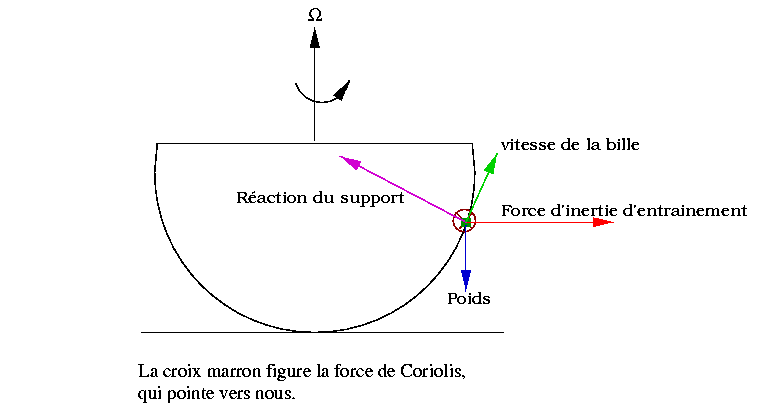
Dans le référentiel tournant, la bille est soumise à son poids, à la force d'inertie d'entraînement, à la force de Coriolis, et à la réaction du support. C'est la force d'inertie d'entraînement qui impose à la bille de monter le long des parois, et la force de Coriolis dévie la bille, donnant ainsi une trajectoire en forme de spirale.
Figure 14. Agrandir l'image
Résultat en vidéo
Après avoir arrêté le tour, on voit une trace de miel qui dévie du méridien de référence, dans le sens prévu par la force de Coriolis.
Source - © 2000 Planet-Terre - ENS de Lyon
Modélisation de l'effet Coriolis
Durée ~ 5min20s.
Retrouvez l'explication du montage dans Expérience sur les forces d'inertie et dans Modélisation de l'effet Coriolis.
Conclusion
Nous avons à présent terminé notre tour d'horizon des différents aspects de la force de Coriolis, qui a ainsi perdu une bonne partie de ses mystères, du moins nous l'espérons.
Il faut toutefois remarquer que la plupart du temps, le référentiel terrestre peut être pris avec une bonne approximation comme galiléen : c'est le cas par exemple dans les expériences dont la durée est très petite devant la période de révolution de la Terre. Dans ce cas, la force de Coriolis n'intervient pas dans les lois de la mécanique. Nous avons vu qu'il faut utiliser par exemple des pendules dont la période est spécialement grande pour pouvoir voir les effets de la force de Coriolis (pendule de Foucault). Mais il est parfois indispensable de la prendre en compte pour pouvoir expliquer certains phénomènes naturels de grande échelle, comme les mouvements atmosphériques.
Si la vitesse de rotation de la Terre était plus grande, alors cette approximation ne serait pas valable et il faudrait tenir compte de cette force dans notre vie quotidienne ! D'ailleurs, dans Le Petit Prince, Antoine de Saint-Exupéry imagine une planète habitée par un allumeur de réverbère : cette planète doit avoir 3 mètres de circonférence environ, et fait un tour sur elle-même en une minute. En supposant que la pesanteur sur cette planète imaginaire soit la même que sur Terre (ce qui est difficilement réalisable...), on trouve que la force de Coriolis y est environ 1500 fois plus intense que sur Terre ! Avec une telle rotation, la pauvre allumeur de réverbère doit sans cesse prendre tenir compte de la force de Coriolis pour prévoir ses mouvements...
Bibliographie
- J.N. Boyd, P.N. Raychowdhury, Coriolis acceleration without vectors, Am.J.Phys. 49(5), p498, 1981. doi:10.1119/1.12493.
- G.I. Opat, The precession of a Foucault pendulum viewed as a beat phenomenon of a conical pendulum subject to a Coriolis force,Am.J.Phys. 59(9), pp822-823, 1991. doi:10.1119/1.16729.
- P. Mohazzabi, Free fall and angular momentum, Am.J.Phys. 67(11), pp1017-1020, 1999. doi:10.1119/1.19163.
- P. Causeret, Lavabo, Coriolis et rotation de la Terre, CC 88 Hiver 1999-2000, pp 11-14
- M.S. Tiersten, H. Soodak,Dropped objects and other motions relative to the noninertial earth, Am.J.Phys. 68(2), pp129-142
- A.G. Schmidt, Coriolis acceleration and conservation on angular momentum, Am.J.Phys. 54(8), pp 755-757
- J. Walker, « Le carnaval de la physique », édition Dunod, 1997. ISBN-13: 978-2100034796.
- I. Berkes, « La physique de tous les jours », édition Vuibert, (6ème édition) 2006. ISBN-13: 978-2711771677.