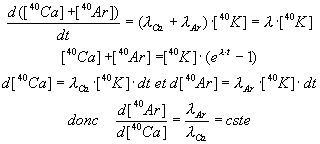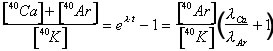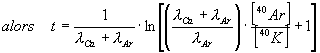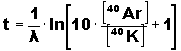Article | 06/10/2003
La méthode de datation potassium-argon
06/10/2003
Résumé
Principe de la méthode de datation K/Ar, équations de la désintégration du 40K.
Table des matières
Principe
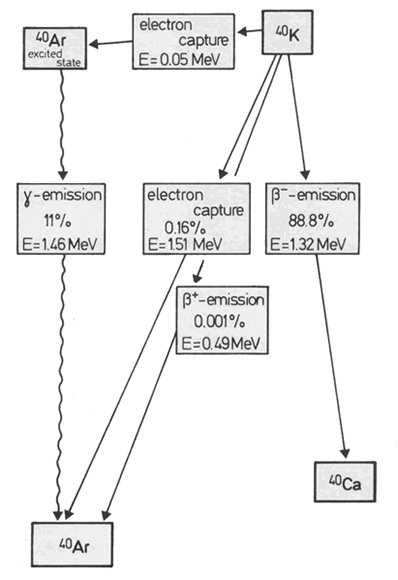
La désintégration du 40K n'est pas simple mais suit plusieurs voies qui sont schématisées dans la figure ci-dessous :
Figure 1. Les voies de désintégration du 40K
- Une voie mène au 40Ca par désintégration β- (et représente plus de 88 % de la désintégration du 40K.
- Une autre voie, elle-même complexe mène au 40Ar, essentiellement par capture électronique (EC).
Il faut tenir compte dans les formules de calcul du temps de ces deux voies de désintégration, en utilisant une constante de désintégration totale, égale à 5,543.10-10 an-1.
Les scientifiques qui travaillent sur la méthode K/Ar utilisent les valeurs recommandées par une commission de spécialistes réunis en 1976 (Subcommission for Geochronology of the IUGS). Ces valeurs ont été publiées par R.H. Steiger et E. Jäger en 1977 (Subcommission on geochronology : Convention on the use of decay constants in geo- and cosmochronology. Earth and Planetary Science Letters, 36, 3, 359-362).
Figure 2. Les constantes de désintégration
Seuls sont considérés comme valides et comparables les âges calculés avec ces constantes et ces abondances isotopiques.
Les désintégrations du potassium 40
Le potassium 40K se décompose en 40Ar et en 40Ca, selon deux réactions qui ont lieu en parallèle, avec deux constantes radioactives et deux périodes différentes.
Transformation 1 :
40K → 40Ca + e-, avec une constante de désintégration de λCa = 4.96 10-10 an-1 (période TCa d'environ 109 ans) ; c'est la radioactivité β classique dont parlent les programmes de physique. Mais une partie des électrons ainsi produits peuvent réagir avec le 40K, pour aboutir à une seconde transformation :
Transformation 2 :
40K + e- → 40Ar, avec une constante de désintégration de λAr = 0,58.10-10 an-1 = 5,8.10-11 an-1 (période TAr d'environ 1010 ans).
Environ 88 % des atomes de potassium 40 suivent la transformation 1, et donc seulement 12 % la transformation 2. Si on s'intéresse à la période de désintégration du 40 K, il faut évidement donner la période la plus courte : la moitié du 40K disparaît en 109 ans (transformation 1 avec la constante en 10-10), pas en 1010 ans (transformation 2 avec la constante de 10-11). Mais dans les équations, il faut écrire que seul 10 % des atomes se transforment en argon....
On peut aussi prendre la seule période (ou constante de désintégration) qui donne l'argon, mais ce n'est pas très logique de dire que la période du 40K est de 1010 ans alors qu'en réalité, la moitié du potassium K se désintègre et disparaît en 109 ans.
Certains livres donnent la période en 109 ans, sans préciser qu'il faut ne prendre en compte que 10 % des désintégrations du potassium, d'où les problèmes que l'on rencontre au moment des calculs... Les équations qu'il faut comprendre et appliquer sont présentées dans la partie suivante.
Les équations à utiliser pour dater par la méthode Potassium Argon
40K → 40Ar par désintégration β+ et 40K → 40Ca par désintégration β-.
Les deux réactions ont lieu en parallèle mais avec des constantes bien différentes : λAr = 0,58.10-10 an-1 = 5,8.10-11 an-1 et λCa = 4,96.10-10 an-1, soit presque dix fois plus.
[40Ca] + [40Ar] = [40K]0 - [40K] (1)
Or [40Ar]0=0 (l'argon étant un gaz, il s'échappe facilement du réseau cristallin lors de la cristallisation à température élevée).
Posons λ = λCa + λAr.
On obtient ainsi :
d'où [40Ar] / [40Ca] = λAr / λCa(2).
Expressions du temps :
soit, en simplifiant :
( λCa + λAr ) / λAr = λ / λAr = 5,54.10-10 / 0,58.10-10 ≈ 10 d'où :
Si l'on suit la définition stricte de la période radioactive, temps au bout duquel la moitié de l'élément père 40K, a disparu, cette période vaut bien, d'après (1) :
On constate donc que la constante λ est la somme de ces deux constantes λCa et λAr, et l'équation à utiliser pour le calcul est un peu moins simple que pour le couple Rb-Sr.