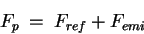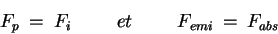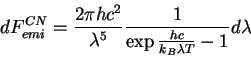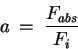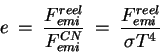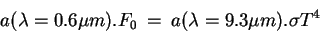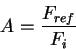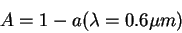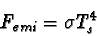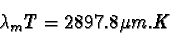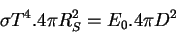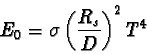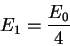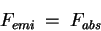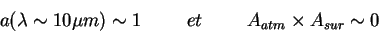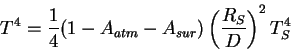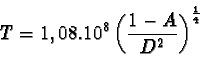Article | 21/10/2003
Le rayonnement thermique et la loi du Corps Noir
21/10/2003
Résumé
Première partie du cours sur le rayonnement thermique, l'effet de serre et le bilan radiatif de la Terre.
Table des matières
- Les différents processus de transfert de la chaleur
- Caractéristiques du rayonnement thermique
- Émission, absorption, réflexion-diffusion, transparence et opacité
- Relations entre les flux lumineux, notion de rayonnement d'équilibre
- Définition du « corps noir », lois de Planck, de Wien et de Stephan
- Rayonnements à partir de surfaces réelles
- Application à une surface réelle éclairée par le Soleil, notion d'albédo
- Applications
Les différents processus de transfert de la chaleur
La conduction
Il s'agit du transfert de la chaleur d'un endroit à l'autre d'un milieu, sous l'influence d'un gradient de température, sans mouvements macroscopiques. La conduction est d'autant plus facilement observable que les mouvements macroscopiques sont inhibés. On l'observe donc principalement dans les solides.
Prenons l'exemple d'une barre métallique que l'on chauffe à l'une de ses extrémités : l'agitation thermique des atomes situés à l'extrémité chauffée de la barre augmente et se transmet de proche en proche dans la direction inverse du gradient thermique.
Dans les métaux, la conduction fait intervenir les électrons libres qui les rendent bons conducteurs de la chaleur. En revanche dans les isolants, la conduction se fait mal. En résumé, il y a une forte correspondance entre les propriétés thermiques et électriques des solides.
La conduction s'observe aussi dans des fluides au repos mais elle est beaucoup plus faible que dans un métal. De plus, elle est souvent dominée par la convection.
La convection
La convection implique le transport de la chaleur par une partie d'un fluide qui se mélange avec une autre partie. La convection concerne exclusivement les fluides (gaz ou liquides) puisqu'elle prend sa source dans un transport macroscopique de matière.
La convection a lieu par exemple lorsque l'on chauffe une casserole d'eau. Le gradient thermique vertical est dirigé vers le bas. La masse volumique du fluide inférieur s'abaisse (car celui ci est plus chaud) et le fluide s'élève pour être remplacé par du fluide plus lourd situé plus haut. La convection tente de s'opposer au gradient thermique par un mouvement de fluide.
Ce processus est s'associe à l'action de la gravité. On note que si l'on chauffe la casserole par le haut, le fluide chaud se situe au dessus du fluide froid et la convection est annihilée. Les Shadoks seraient bien surpris de voir qu'il faudrait un jour pour faire bouillir une casserole d'eau en la chauffant par le haut (seule la conduction intervient).
En gardant cette image dans la tête, on s'aperçoit immédiatement que la convection est importante dans l'atmosphère (les phénomènes de brises thermiques par exemple) puisque l'atmosphère est principalement chauffé par la Terre (nous verrons qu'il absorbe très peu le rayonnement solaire).
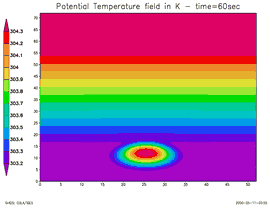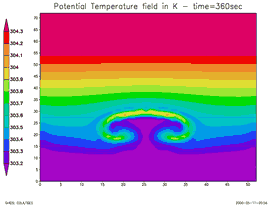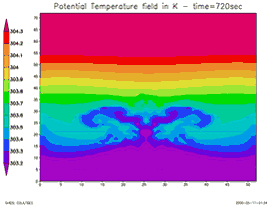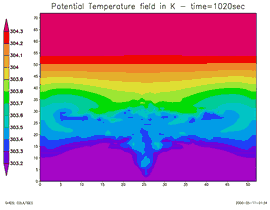
Cette animation présente une coupe verticale de l'atmosphère :
- Axe des abscisses : la surface terrestre
- Axe des ordonnées : la verticale
Les couleurs représentent le champ de température « potentielle » en Kelvin (T(°C) = T (K) - 273). À l'instant initial, on introduit une bulle chaude (couleur rouge) dans une atmosphère stratifiée (le « chaud » est en haut : situation stable) En revanche, les océans chauffés par le haut présentent peu de phénomènes de convection.
Le rayonnement thermique
Un corps chauffé émet de l'énergie sous forme de rayonnement électromagnétique. Une des particularités de ce rayonnement dit "thermique" est qu'il peut se propager dans le vide.
Au niveau microscopique, ce phénomène ne peut s'expliquer en physique classique. Cependant, on retiendra comme image que plus la température du corps est élevée, plus l'agitation thermique responsable de l'émission est élevée.
Comme tout rayonnement électromagnétique, le rayonnement dit thermique est caractérisé par une densité d'énergie et un spectre (répartition de l'énergie suivant la longueur d'onde).Le rayonnement thermique se déplace vers les courtes longueurs d'ondes quand la température du corps augmente.
Ainsi le filament de tungstène utilisé dans les lampes à incandescence a une couleur caractéristique de sa température. A faible température, il est rouge-orangé, puis jaune puis blanc. Le pic du spectre d'émission se déplace de la limite entre l'infra-rouge et le visible (rouge) vers le milieu du visible (blanc).
Il faut finalement distinguer la nature des récepteurs de ce rayonnement thermique : certains le réfléchissent d'autres l'absorbent et la transforment en énergie interne pour rayonner à leur tour.
Conclusion
La Terre étant soumise au rayonnement thermique issu du soleil (seul transfert capable de transporter la chaleur à travers le vide), c'est ce dernier auquel nous allons nous intéresser plus particulièrement dans la seconde section.
Caractéristiques du rayonnement thermique
Cette section se focalise sur le rayonnement thermique. On présente tout d'abord le comportement des surfaces par rapport au rayonnement. On définit ensuite le rayonnement d'équilibre, puis on énonce la loi du corps noir. Enfin on s'intéresse au comportement des surfaces réelles.
Émission, absorption, réflexion-diffusion, transparence et opacité
Nous allons étudier les différents comportements de la matière vis à vis du rayonnement thermique. Nous rappelons que le rayonnement thermique est un rayonnement électromagnétique; on retrouve donc le vocabulaire des ondes.
Émission
Un corps porté à une certaine température convertit son énergie interne (énergie microscopique) en rayonnement thermique. Une unité de surface d'un corps émet durant une unité de temps une quantité d'énergie appelée flux d'émission. On le note Femi.
Absorption
Il s'agit de l'opération inverse. Quand une surface reçoit un flux d'énergie, la fraction transformée en énergie interne est appelée flux absorbé (noté Fabs)
Réflexion et diffusion
Au lieu d'être absorbé, le rayonnement incident sur une paroi peut être directement renvoyé par la paroi. Dans ces conditions on distingue 2 cas.
- Le renvoi obéit aux lois de l'optique géométrique (un angle d'incidence, un angle de réflexion). Il s'agit alors de réflexion.
- Le renvoi se fait dans toutes les directions (même si l'on a une seule direction incidente). On parle alors de diffusion.
On note que l'onde diffusée ou émise a la même fréquence que l'onde incidente. La somme de ces deux flux est notée Fref.
Transparence et opacité
Un milieu peut transmettre intégralement l'onde incidente, il est alors appelé milieu transparent. Le vide est un exemple de milieu transparent. En première approximation, le verre est aussi un milieu transparent pour des longueurs d'ondes dans le domaine du visible. Inversement, un corps ne transmettant aucune partie du rayonnement incident est dit corps opaque.
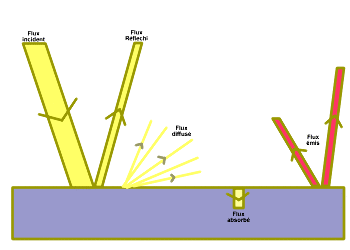
Figure 1. Les différents flux au niveau de la surface d'un corps opaque
On remarque que le flux émis n'est pas forcément à la même longueur d'onde que le flux incident. Rappel des notations du cours pour les flux
Fréf = Fluxréfléchi + Fluxdiffusé ; Fabs = Fluxabsorbé ; Fémi = Fluxémis ; Fi = Fluxréfléchi + Fluxabsorbé ; Fp = Fluxréfléchi + Fluxémis
Relations entre les flux lumineux, notion de rayonnement d'équilibre
Flux incident
Le flux incident Fi est défini comme la puissance surfacique du rayonnement incident en un point considéré de la surface du corps étudié (cf. figure précédente). Le flux incident est soit réfléchi-diffusé, soit absorbé. On a donc la relation suivante :
Flux partant
Le flux surfacique partant du corps est la somme du flux émis et du flux réfléchi. On a donc la relation suivante :
Équilibre radiatif
On dit qu'un corps opaque est en équilibre radiatif avec le rayonnement qui l'entoure, s'il n'emmagasine pas d'énergie ou n'en perd pas. Dans ces conditions, le flux incident doit être égal au flux partant. On a donc :
Définition du « corps noir », lois de Planck, de Wien et de Stephan
Le corps noir
Le corps noir est par définition un corps absorbant intégralement les radiations qu'il reçoit. Dans ces conditions, le flux réfléchi est nul et le flux partant est seulement constitué du flux émis. On a donc :
Loi de Planck
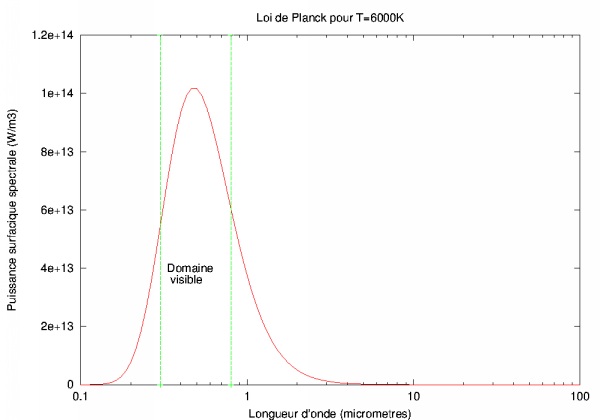
La loi de Planck donne la répartition suivant la longueur d'onde du flux émis Femi d'un corps noir à la température T. Notre but n'est pas de démontrer la loi de Planck, mais elle s'obtient en établissant une relation entre la densité volumique d'énergie électromagnétique du champ rayonné et le flux partant ou incident. Dans un petit intervalle de longueur d'onde, le flux émis Femi a l'expression suivante :
h = 6,63 x 10-34 J.s : constante de Planck ; kB = 1,38 x 10-23 J/s constante de Boltzmann ; c = 3,00 x 108 m/s vitesse de la lumière ; λ : longueur d'onde ; T : Température du corps opaque.
 , on notera la différence d'amplitude des flux malgré l'échelle logarithmique en ordonnée pour
ces courbes de Planck pour le Soleil (T=6000K) et la Terre (T=300K).
, on notera la différence d'amplitude des flux malgré l'échelle logarithmique en ordonnée pour
ces courbes de Planck pour le Soleil (T=6000K) et la Terre (T=300K).Loi de Wien
Cette loi dite du « déplacement de Wien » découle directement de la formule de Planck. Pour une température donnée, elle donne la valeur de la longueur d'onde λm où le flux est maximal :
À l'aide de la figure précédente montrant les courbes de Planck pour les 2 températures, on peut trouver graphiquement que :
- Pour T = 6 000 K, λm = O,6 micromètre (μm), soit le milieu du spectre visible.
- Pour T = 300 K, λm = 10 μm, situé dans infra-Rouge.
On vérifiera ces valeurs en faisant une simple division !!!!
Loi de Stefan
La loi de Stefan est la simple intégration de la loi de Planck sur l'ensemble des longueurs d'onde. Ce peut être un petit exercice de mathématiques qui donne :
avec σ = 5,67 x 10-8 W.m-2.K-4
Vite, des valeurs numériques :
- Pour T = 6 000 K, on a Fp = Fi = 73 000 000 W/m2
- Pour T = 300 K, on a Fp = Fi = 459 W/m2
La formule de Stefan est d'une importance capitale et rappelle que les flux incidents et partants ne sont fonction que de la température. On note la forte dépendance en T puisqu'il s'agit d'une puissance quatrième. Alors que la Température du Soleil n'est que 20 fois plus élevée que celle de la Terre, son flux partant est 160.000 fois plus élevé.
Rayonnements à partir de surfaces réelles
Une surface réelle diffère du Corps Noir pour :
l'absorption. Une surface réelle est caractérisée par son pouvoir absorbant. On note a le coefficient d'absorption. Il s'agit du rapport entre le flux absorbé et le flux incident.
Ce rapport dépend de la longueur d'onde du rayonnement incident. Pour le Corps Noir, il est égal à 1.
l'émission. Une surface réelle est caractérisée par son pouvoir d'émission. On note e le coefficient d'émission. Il s'agit du rapport entre le flux émis réel et le flux émis du corps noir de même température.
Ce rapport dépend de la longueur d'onde du rayonnement émis. Pour le Corps Noir, il est égal à 1.
Pour une même longueur d'onde, le coefficient d'absorption et le coefficient d'émission sont égaux. Cependant, rayonnement incident et rayonnement émis étant souvent dans des domaines de longueur d'ondes très différents, il faudra prendre 2 valeurs différentes.
Tableau 1. Des exemples de coefficients d'absorption en fonction de la longueur d'onde.
Surface | 0,6 μm - solaire | 1,8 μm - 1 650K | 3,6 μm - 800K | 5,4 μm - 430K | 9,3 μm - 310K |
Fer galvanisé | 0,89 | 0.90 | 0,28 | ||
Marbres blancs | 0,47 | 0,97 | |||
Verre | 0,1 | 0,90 | |||
Papier blanc | 0,28 | 0,25 | 0,82 | 0,95 | |
Océan | 0,9 | ||||
Sol enneigé | 0,3 | ||||
Végétation | 0,8 | 0,85 |
Application à une surface réelle éclairée par le Soleil, notion d'albédo
On considère une surface terrestre boisée éclairée par un flux solaire F0. Cette surface est à une température T proche de 300K. Son spectre d'émission se situe donc dans l'infrarouge. Écrivons l'égalité des flux absorbés et émis pour cette surface.
On peut trouver T en connaissant les valeurs numériques de F0 et de a aux 2 longueurs d'ondes. Enfin, on appelle albédo (A) le rapport entre le flux réfléchi et le flux solaire incident.
On note que :
Applications
Cette section présente différentes applications des lois de Planck, Stefan, Wien et de la loi du corps noir.
Calcul de différents paramètres du rayonnement solaire
On assimile le Soleil à un corps noir à la température T = 6 000 K (on note que l'on peut trouver dans certains ouvrages TS = 5 500K).
Calcul de la puissance émise par un mètre carré de la surface du soleil.
Le Soleil est un corps noir, donc son flux d'émission (Fémi) obéit à la loi de Stefan. On en déduit que :
Calcul de la puissance émise par la surface du soleil
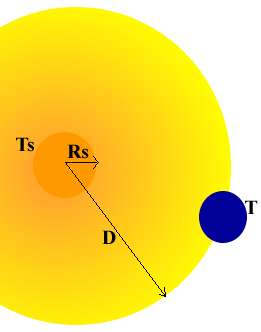
Connaissant le rayon du Soleil (RS=0,7 x 106 km), on en déduit facilement sa surface. On conclut par :
Calcul de la longueur d'onde où le flux solaire est maximal.
Application de la loi de Wien :
On vérifie que pour le soleil (T = 5.770K), le maximum de l'émission se situe dans le visible alors que pour la Terre il se situe dans l'infrarouge.
Calcul de la constante solaire.
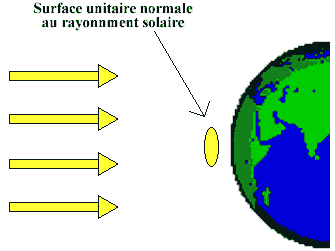
La constante solaire, souvent notée E0, est par définition la puissance reçue du soleil par unité de surface normale aux rayons solaires sur la surface terrestre sans atmosphère (ou au sommet de l'atmosphère). Le soleil émet un rayonnement sphérique. Donc toute la puissance issue initialement de la surface du soleil traverse ultérieurement une sphère de rayon R (à l'instant t = (R - RS) / c). Écrivons donc cette égalité entre les 2 puissance pour la sphère de rayon D (D=distance Terre-Soleil) :
La constante solaire vaut donc :
On note que la puissance solaire moyenne reçue par unité de surface terrestre E1 est 4 fois moins élevée. On écrit que la puissance reçue par le disque terrestre est répartie sur la sphère terrestre :
Calcul de la température des planètes avec atmosphère non absorbante
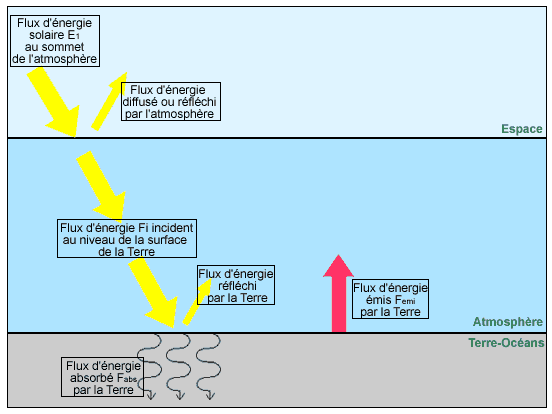
On considère une planète du système solaire située à une distance D du soleil. L'albédo de cette planète est du à son atmosphère (Aatm) et à sa surface (Asur). On postule que l'atmosphère n'absorbe pas le rayonnement solaire (elle n'émet donc pas de rayonnement à sa température).
- Flux d'énergie solaire E1 au sommet d*e l'atmosphère. On sait d'après l'exercice précédent, qu'en moyenne, une surface unité située au sommet de l'atmosphère reçoit un flux d'énergie E1 égal à : E1 = (1/4).σ.(RS/D)2.T4S
- Flux d'énergie diffusé ou réfléchi par l'atmosphère. Fratm = Aatm.E1
- Flux d'énergie Fi incident au niveau de la surface de la Terre : Le flux incident au niveau de la surface de la planète est la différence entre le flux incident au sommet de l'atmosphère (E1) et le flux diffusé réfléchi (Aatm.E1) : Fi = (1 - Aatm).E1
- Flux réfléchi par la Terre. FrTerre = Asur.E1.(1 - Aatm)
- Flux d'énergie Fémi par la Terre. Le flux émis par la Terre est donnée par la loi d'émission des corps réels : Femi = a.λ.(∼10 μm)σT4
- Flux d'énergie absorbé Fabs par la Terre. Fabs = (1 - Aatm)(1 - Asur).E1
La température d'équilibre radiatif de la planète s'obtient en écrivant l'égalité entre les flux absorbés et émis : | |
On fait les approximations suivantes et on additionne l'albédo de l'atmosphère et de la surface dans une variable A : | |
On obtient alors l'égalité suivante : |
On obtient alors 2 expressions équivalentes donnant la température de surface de la planète en fonction de l'albédo total A et de la distance planète-Soleil en mètres
La température calculée pour la Terre est inférieure de 33 K à la température observée (TOBS = 287 K). L'absorption des radiations infrarouges émises par la Terre par les molécules atmosphériques est responsable de cette différence.
Sachant que la Terre est une ellipse dont le rayon varie entre 147 (au périhélion) et 152 (à l'aphélion) millions de km, calculez la variation relative de la température de la surface terrestre entre ces 2 points de l'orbite terrestre.
Mise en évidence de l'albédo de la surface terrestre
On rappelle que l'albédo est la fraction du rayonnement solaire directement renvoyé vers l'espace (réflexion ou diffusion) par la surface terrestre ou par l'atmosphère. Si l'on place sur un satellite en orbite autour de la Terre un capteur lumineux sensible seulement aux longueurs d'ondes visibles, il ne verra que le rayonnement solaire réfléchi ou diffusé par la Terre.
En première approximation, on peut dire que la radiance d'un pixel d'une image satellite « canal visible » varie de la même manière que l'albédo de la surface représentée (plus le pixel est clair plus l'albédo de la surface est élevé).
On ne veut s'intéresser qu'à l'albédo de la surface terrestre. Pour cela, on cherche une région où l'atmosphère est assez sèche pour que la vapeur d'eau n'ait pas d'influence sur les radiations réfléchies par la surface terrestre. La région du Sahel est particulièrement sèche durant l'hiver dans l'hémisphère Nord.
- Remarques générales sur la totalité de l'image : l'image « canal visible » est prise le 1er Janvier 1999 à 12h00 GMT par le satellite géostationnaire Météosat 7. Autour de ces longitudes, il s'agit d'une période diurne puisque l'image est n'est pas noire. On note la différence d'albédo entre l'Océan Atlantique (pixels foncés) et le continent africain (pixels clairs). Ceci est le reflet des différences de coefficient d'absorption entre l'océan (coefficient d'absorption de 0,9, soit un albédo de 0,1) et le sol qui a un albédo plus élevé. Cette différence est d'autant plus notoire à la latitude de la Mauritanie où le sol est sablonneux et présente un fort albédo. On note enfin que plus on se rapproche de l'équateur, plus les pixels deviennent foncés. La forêt équatoriale présente un albédo faible.
- Remarques sur la zone située au voisinage de Dakar (extrême Ouest). Avec une meilleure résolution, on observe mieux le net contraste entre océan et continent. On distingue nettement au centre de l'image la vallée du fleuve Sénégal où la végétation diminue l'albedo.
- Remarques sur la zone centrée sur le fleuve Niger. Comme précédemment, la vallée est marquée en noir sur l'image.
- Remarques sur la zone centré sur le lac Tchad. Il est aussi bien visible et montre le faible albedo d'une surface aquatique.
- Remarques sur la zone centrée sur le Nil. Le parcours du fleuve est encore très net, et on remarque le faible albedo de la Mer Rouge.
Vers la suite du cours : Interactions du rayonnement solaire avec l'atmosphère.
Vers la fin du cours : Bilan radiatif de la Terre