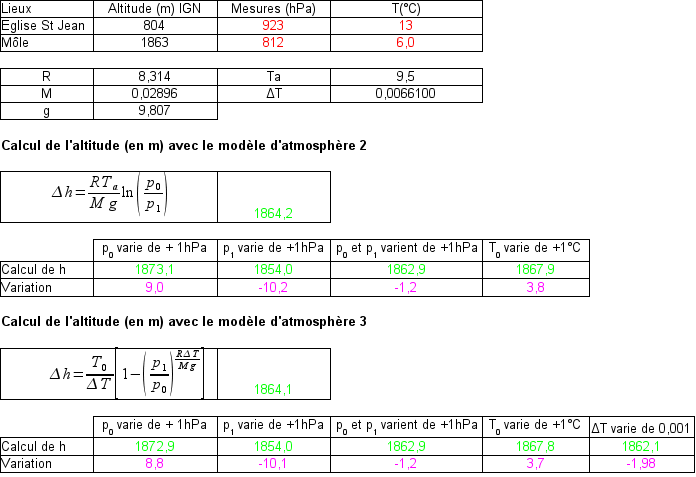Outils personnels
Navigation

Aller au contenu. | Aller à la navigation

Vous êtes ici : Accueil → Ressources → Détermination de l'altitude des montagnes par la méthode barométrique

Article | 25/11/2011

Détermination de l'altitude des montagnes par la méthode barométrique

25/11/2011

Vincent Deparis

Lycée Jean Monnet - Annemasse
 

Olivier Dequincey

ENS de Lyon / DGESCO

Résumé

Dans cet article, nous présentons la détermination de l'altitude d'une montagne par la méthode barométrique, mise en œuvre par quatre élèves de première scientifique (Arthur, Dimitri, François-Xavier et Lucas) dans le cadre d'un atelier scientifique. La méthode n'est plus utilisée aujourd'hui du fait de son manque de précision. Elle n'en reste pas moins intéressante d'un point de vue pédagogique car elle est très formatrice pour la démarche scientifique : établissement de la formule du nivellement barométrique, élaboration d'un protocole des mesures, obligation de la simultanéité des mesures, attention à la précision des instruments et à la qualité des mesures, nécessité de prendre en compte des corrections multiples (influence de la température de l'air).

Table des matières

Introduction

L'air atmosphérique, comme tous les corps, est attiré par la Terre et son poids est à l'origine de la pression atmosphérique. En gagnant de l'altitude, la pression atmosphérique diminue puisque l'épaisseur de la colonne d'air s'amincit. L'idée, émise pour la première fois par Blaise Pascal en 1647, est de se servir de cette diminution de la pression atmosphérique pour déterminer une différence d'altitude entre le sommet d'une montagne et un point de référence, d'altitude connue. Cette méthode de nivellement barométrique nécessite donc l'ascension de la montagne puisqu'elle impose deux mesures de pression simultanées, au sommet et à la base de la montagne. Elle nécessite également une relation, appelée formule de nivellement barométrique, qui permette de convertir la différence observée de pression en une différence d'altitude.

Cette méthode a été mise en oeuvre par 4 élèves du lycée Jean Monnet d'Annemasse, pour déterminer l'altitude du Môle (Haute Savoie), sommet proche, situé à environ 15 km au Sud-Est d'Annemasse.

Les formules barométriques

L'établissement des formules du nivellement barométrique est classique. Nous redonnons les étapes essentielles pour faire ressortir les points clés.

"Périer mesurant la hauteur du tube de Toricelli sur le haut du Puy de Dôme"

Source - © 1867 Louis Figuier

Figure 1. "Périer mesurant la hauteur du tube de Toricelli sur le haut du Puy de Dôme"

Cette gravure illustre l'expérience menée par Périer en septembre 1648, sur demande de Pascal. Le but était la détermination de la variation de pression en fonction de la variation d'altitude (base et sommet du Puy de Dôme). Répétée en d'autres lieux, cette mesure permit à Pascal de proposer une première relation linéaire simple entre altitude et pression (variation de hauteur de mercure dans un tube de Toricelli).

Source : Les merveilles de la science, Louis Figuier, 1867, fig.18 p.33


Les relations de départ et les paramètres pris en compte

Variation de pression due à une variation élémentaire dh de hauteur


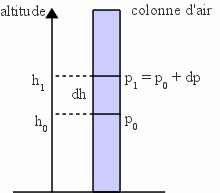
Si l'on considère une colonne d'air de surface S, la pression atmosphérique p en un point de la colonne est égale au poids de la colonne d'air supérieure divisé par cette surface S. L'axe vertical étant orienté vers le haut, la variation de pression entre les altitudes h0 et h1 provient de la contribution du volume élémentaire d'air dV compris entre les deux altitudes, soit :

  • dp = p1-p0 = - ρ.dV.g/S = -ρ.g.dh,

dp est négatif, la pression baisse lorsque l'altitude augmente.

Pour une variation de hauteur donnée, la variation de pression ne sera pas la même au niveau du Mont-Blanc et au niveau de la mer, pour deux raisons.

  1. D'abord parce que la pesanteur g dépend de l'altitude (g = G.MT/(RT+h)2) mais cette variation est faible et nous la négligerons par la suite.
  2. Ensuite, parce que la densité de l'air est fortement variable avec l'altitude. C'est de ce paramètre que proviennent toutes les difficultés futures.

La densité de l'air

L'atmosphère est une enveloppe composée d'un mélange de gaz. La proportion des gaz est constante car l'atmosphère est brassée par les vents. Elle est donnée pour l'air sec dans le tableau ci-dessous.

Tableau 1. Composition de l'air

Gaz

Proportion en volume

diazote

78,084

dioxygène

20,946

argon

0,934

dioxyde de carbone

0,035

autres : néon, hélium, krypton, dihydrogène, etc

0,001


En supposant que l'air réagit comme un gaz parfait, on peut écrire pour un volume élémentaire dV : p.dV = n.R.T. Comme n=m/M=(ρ.dV)/M, il vient alors

  • ρ = (p.M)/(R.T) ;

avec la constante des gaz parfaits R=8,314 J.K-1.mol-1, T la température en Kelvin, n le nombre de moles de gaz contenu dans le volume dV, M la masse molaire moyenne dea gaz de l'atmosphère, M=0,02896 kg.mol-1 [M=0,78084.M(N2) + 0,20946.M(O2) + 0,00934.M(Ar) +0,00035.M(CO2)].

La densité de l'air dépend essentiellement de deux paramètres.

  1. La pression. L'air est compressible et est d'autant plus dense que la pression qui le comprime est forte. Les couches inférieures de l'atmosphère, comprimées par les couches supérieures, sont donc plus denses que celles-ci.
  2. La température. L'air, comme tous les corps, se dilate ou se contracte en fonction de la température. Plus la température baisse (plus l'altitude augmente), plus l'air se contracte et plus sa densité augmente. Les deux paramètres (pression et température) jouent donc en sens inverse l'un de l'autre.

Variation de la température dans l'atmosphère

L'atmosphère est découpée en plusieurs couches, caractérisées par la variation de la température. Seule la première couche, appelé troposphère, nous intéresse. Son épaisseur varie de 7 km dans les régions polaires à 18 km à l'équateur. C'est la couche concernée par les phénomènes météorologiques. Dans la troposphère, on observe que la température décroît linéairement avec l'altitude. Son gradient thermique vertical (défini pour l'air ambiant stable, sans mouvements verticaux ou horizontaux) est variable en fonction des masses d'air : dans des masses d'air chaud, il est de 0,3 à 0,5°C pour 100 m de montée ; pour les masses d'air froid, il prend des valeurs de 0,6 à 0,8°C pour 100 m. En moyenne, il vaut 0,65°C pour 100 m.

Si T0 est la température à une station inférieure, ΔT le gradient thermique et Δh la différence d'altitude entre la station inférieure et une station supérieure, la température T à la station supérieure est donnée par : T = T0 - ΔT x Δh.

Différents modèles d'atmosphère

Trois modèles d'atmosphère différents sont classiquement envisagés.

  • Modèle 1. La densité de l'air est constante quelque soit l'altitude. C'est l'hypothèse la plus simple.
  • Modèle 2. La densité de l'air ne dépend que de la pression (la température de l'atmosphère est constante : Ta = 15°C = 288 K).
  • Modèle 3. La densité de l'air dépend de la pression et de la température. On suppose que la température varie linéairement, suivant une loi du type : T(h) = T0 - ΔT x (h-h0), où ΔT est le gradient thermique entre les deux altitudes et T0 la température à la station inférieure. Dans ces modèles, l'humidité de l'air n'est pas prise en compte.

Intégration des relations précédentes

Pour établir les lois de la variation de la pression avec l'altitude, il faut intégrer l'expression dp =-ρ.g.dh, en tenant compte des différents modèles pour la variation de la densité avec l'altitude. Nous appelons p1, p2, p3 les pressions à l'altitude h obtenues à partir, respectivement, des modèles d'atmosphère 1, 2 et 3 décrit ci-dessus.

La densité de l'atmosphère est uniforme (modèle 1)

L'intégration donne : p0∫p1 dp = h0∫h - ρ.g.dh = - ρ.g. h0∫h dh, soit p1 = p0 - ρ.g.Δh, soit, encore, une différence d'altitude Δh = (p0 - p1)/(ρ.g).

La température de l'atmosphère est constante (modèle 2)

La relation dp = -ρ.g.dh devient, en remplaçant ρ, dp = -(p.M)/(R.Ta).g.dh, soit encore dp/p = -(M.g)/(R.Ta).dh.

L'intégration donne alors : p0∫p2 dp/p = h0∫h - (M.g)/(R.Ta).dh = - (M.g)/(R.Ta).h0∫h dh, puisque (M.g)/(R.Ta) est constant.

On obtient : ln(p2/p0) = - (M.g)/(R.Ta).(h-h0) = - (M.g)/(R.Ta).Δh, soit, si l'on s'intéresse à la pression, p2 = p0.exp[- (M.g)/(R.Ta).Δh ].

De cette intégration, on obtient aussi la différence d'altitude qui s'exprime alors par Δh = (M.g)/(R.Ta).ln(p0/p2).

La température de l'atmosphère décroît linéairement (modèle 3)

La température suit dans ce cas une loi du type T(h) = T0 - ΔT x (h-h0), où ΔT est le gradient thermique entre les deux altitudes.

L'intégrale devient :

  • p0∫p3 dp/p = - (M.g)/R.h0∫h dh/T = - (M.g)/R.h0∫h dh/(T0 - ΔT x (h-h0).

Comme ∫dx/(b-ax) = 1/a.ln(b-ax), on obtient :

  • h0∫h dh/(T0 - ΔT x (h-h0) = 1/ΔT.[ ln(T0 - ΔT x (h-h0)) - ln(T0) ] = 1/ΔT.ln(1 - ΔT x Δh/T0)

Ce qui aboutit, pour l'intégrale de départ, à :

  • p3 = p0.(1 - ΔT x Δh/T0)(M.g)/(R.ΔT) ;
  • ou, si l'on extrait la différence d'altitude, Δh = T0/ΔT.[ 1 - (p3/p0)(R.ΔT)/(M.g)].

Courbes donnant les variations de pression en fonction de l'altitude

Nous considérons l'atmosphère standard, caractérisée par les données suivantes :

  • pression au niveau de la mer : p0 = 1013 hPa ;
  • température au niveau de la mer : T0 = Ta = 15°C = 288 K ;
  • gradient thermique vertical : ΔT = 0,006500 K/m ;
  • pesanteur : g = 9,807 m.s-2 ;
  • masse molaire moyenne de l'air : M = 0,02896 kg.mol-1.

Les expressions précédentes deviennent, lorsque les pressions sont exprimées en hPa :

  • Modèle 1 : p1 = 1013 - 1,1201.Δh ;
  • Modèle 2 : p2 = 1013.exp(- Δh/8431) ;
  • Modèle 3 : p3 = 1013.(1 - 0,0065.x Δh/288)5,255.
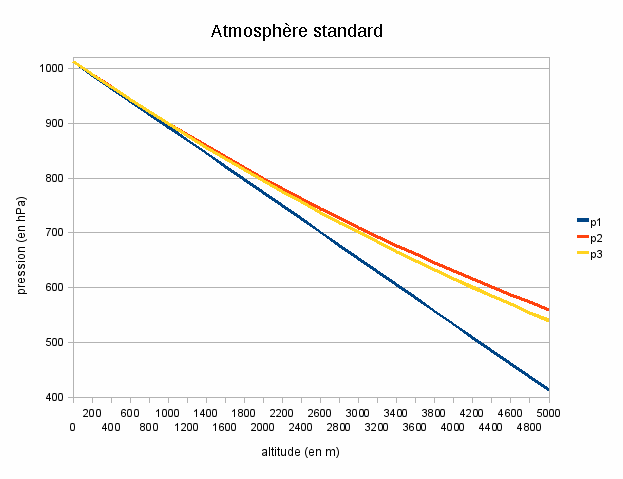
Variation de la pression avec l'altitude en fonction de différents modèles d'atmosphère

Figure 3. Variation de la pression avec l'altitude en fonction de différents modèles d'atmosphère

Courbes pour 3 modèles : p1 = densité constante, p2 = densité fonction de la pression, p3 = densité fonction de pression et température avec décroissance linéaire de la température.


Pour le modèle 1, la variation de pression est linéaire. En effet, la densité de l'atmosphère étant constante, toutes les couches, quelque soit leur altitude, ont la même contribution. Ce n'est plus vrai pour les modèles 2 et 3. Plus l'altitude est importante, moins la variation de pression pour une variation de hauteur donnée est grande. En effet, les couches supérieures, étant de moins en moins comprimées, sont de moins en moins denses et contribuent donc de moins en moins à la pression. Par exemple, les couches d'air au niveau du sommet du Mont Blanc ont une contribution presque deux fois plus faibles que les couches au niveau de la mer. Pour le modèle 3 (la température varie), les variations de pression pour un Δh donné sont légèrement plus fortes que pour le modèle 2 (la température est constante). En effet, plus on monte en altitude, plus les couches d'air sont froides et donc plus elles sont contractées et denses. L'effet de la température contrebalance un peu l'effet de la pression.


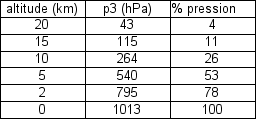
Dans le cadre du modèle 3, on remarque que les 5 premiers kilomètres d'altitude sont responsables de 47% de la pression qui règne au niveau de la mer. Les 5 suivants (de 5 à 10 km) de 27%, puis de 10 à 15 km de 15%, puis de 15 à 20 km de 7%. Ces chiffres illustrent encore une fois que les couches supérieures ont de moins en moins d'importance dans la pression ressentie au niveau de la mer.

Vérification expérimentale des formules barométriques

Le but est de relier les variations de pression à des variations d'altitude. Mais la pression atmosphérique varie aussi sans que l'on change d'altitude ! Ce sont les variations d'origine météorologique, qui, sur une journée, sont de l'ordre de quelques hectopascals, à moins d'un changement de temps très brutal. Ces variations proviennent d'une modification de la masse d'air ambiante : passage d'une dépression ou d'un anticyclone, arrivée d'air chaud ou froid, d'air sec ou humide, etc. Pour s'affranchir des phénomènes météorologiques, il est nécessaire de réaliser des mesures de pression simultanées en des points proches : les variations de pression proviennent ainsi uniquement de la hauteur de la couche d'air comprise entre les points de mesure. Cependant, les pressiomètres classiques ne sont pas compensés en température (la valeur indiquée de la pression dépend de la température du capteur) et ne permettent donc pas des mesures en extérieur. En revanche, les montres altimètres sont compensées en température et, à la condition d'en avoir plusieurs de même marque, elles permettent des mesures simultanées (nous en avions deux à disposition).

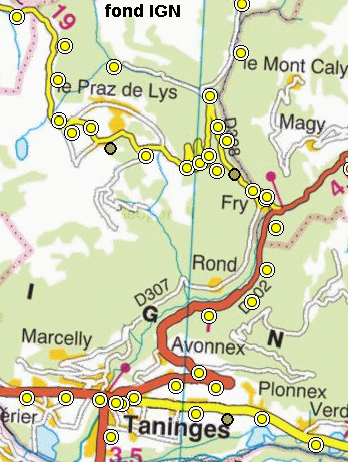
Nous avons donc effectué six mesures presque (!) simultanées de pression (30 minutes d'écart) en six points d'altitude différente le long de la route Taninges – Praz de Lys (Haute Savoie), à quelques kilomètres à l'Est du Môle. Cette route a été choisie parce qu'elle présente un dénivelé important, environ 1000 m, assez rapidement et parce qu'on y trouve de nombreux repères de nivellement de l'IGN, d'altitude parfaitement connue.



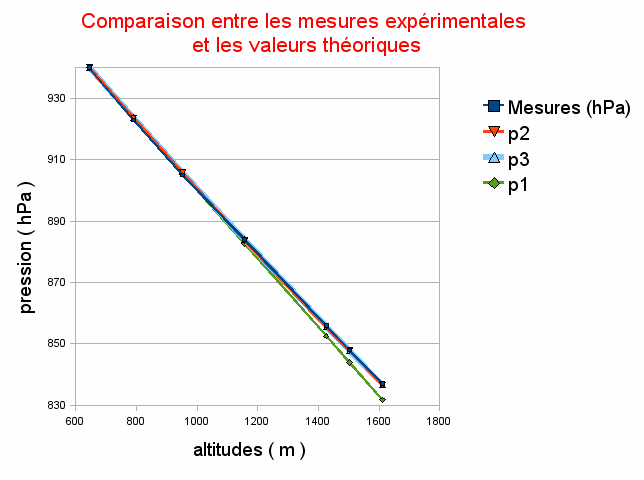
Le tableau ci-dessous donne les mesures réalisées et les valeurs théoriques calculées à partir des 3 modèles d'atmosphère décrits. La figure 5 montre que le modèle 1 (densité de l'air constante) s'écarte fortement des mesures mais que les modèles 2 (température constante) et 3 (décroissance linéaire de la température) sont tout aussi valables l'un que l'autre : le dénivelé de 1000 m entre le col et l'église de Taninges n'est pas suffisant pour les départager.


Mesure de la variation de la pression avec l'altitude et comparaison avec les valeurs théoriques

Figure 6.  Mesure de la variation de la pression avec l'altitude et comparaison avec les valeurs théoriques

Mesures (carrés bleus) comparées aux valeurs théoriques des 3 modèles envisagés : p1 = densité constante, p2 = densité fonction de la pression, p3 = densité fonction de pression et température avec décroissance linéaire de la température.


Application : détermination de l'altitude du Môle (Haute Savoie)

Repère de nivellement de l'église de Saint Jean de Tholome

Source - © 2011 Vincent Deparis

Figure 7. Repère de nivellement de l'église de Saint Jean de Tholome

Avec 804,001 m d'altitude, ce repère est le lieu de la mesure de référence.


Pour déterminer l'altitude du Môle avec des mesures barométriques, il faut réaliser des mesures simultanées de pression et de température de l'air, au sommet et à la base de la montagne, en un point d'altitude connue. Ce point bas a été pour nous l'église de Saint Jean de Tholome, où l'on trouve un repère de nivellement de l'IGN (804,0 m d'altitude). Les mesures et les calculs sont données dans le tableau ci-après.


Les résultats paraissent satisfaisants   l'altitude du Môle est retrouvée à un mètre près ! Mais il s'agit plus d'une coïncidence qu'autre chose, comme le montrent les calculs de sensibilité, qui indiquent que le résultat est au mieux à ± 10 m !

Expliquons qualitativement les résultats trouvés dans ces calculs de sensibilité.

  • Si p0 augmente de 1 hPa : la variation de pression Δp augmente donc Δh augmente (cela revient à descendre la station inférieure).
  • Si p1 augmente de 1 hPa : la variation de pression Δp diminue donc Δh diminue (cela revient à descendre la station supérieure).
  • Si p0 et p1 augmentent de 1 hPa : la variation de pression Δp ne varie pas mais Δh diminue quand même. En effet, l'augmentation des deux pressions revient à être plus près du niveau de la mer où les couches d'air, plus denses, contribuent davantage à la pression.
  • Si T0 augmente de 1°C : l'air est plus chaud, donc moins dense. Il faut une couche d'air plus épaisse pour expliquer le même Δp et donc Δh augmente.
  • ΔT augmente de 0,001 : le gradient est plus fort, la température diminue plus rapidement, l'air devient plus dense et donc Δh diminue.

Lorsqu'on utilise la méthode barométrique, les sources d'erreurs sont nombreuses. Elles peuvent provenir des mesures effectuées : précision de la montre altimètre, étalonnage de la montre altimètre, difficulté de la mesure de la température de l'air (pour se mettre à l'abri du vent et avoir une mesure fiable). Elles peuvent aussi provenir des lois mathématiques utilisées : celles-ci ne prennent pas en compte l'humidité de l'air et supposent, soit une température de l'atmosphère uniforme, soit une température décroissant linéairement avec l'altitude, ce qui n'est pas toujours le cas (phénomène d'inversion en hiver, temps instable, etc).

Quelques remarques sur les montres altimètres

Fonctionnement d'une montre altimètre

Les altimètres, bien connus des randonneurs, mesurent la pression atmosphérique p3 en un lieu donné, la comparent avec une pression de référence p0 (la pression au niveau de la mer) et convertissent la différence de pression en une différence d'altitude. Le modèle d'atmosphère utilisé est le modèle 3 dans les conditions standards (température au niveau de la mer, T0 = 15°C ; gradient thermique vertical, ΔT = 0,006500 K/m).

La formule employée est donc la suivante : Δh = T0/ΔT.[ 1 - (p3/p0)(R.ΔT)/(M.g)], soit, ici, Δh = 288/0,0065.[ 1 - (p3/p0)1/5,255].

Les montres altimètres sont compensées en température, c'est-à-dire que l'influence de la température de l'air sur le capteur est corrigée. Les altimètres nécessitent un calage puisqu'en un lieu donné, la pression atmosphérique change suivant les conditions météorologiques. Le calage consiste à faire coïncider l'altitude calculée par l'altimètre avec l'altitude connue d'un lieu. Cela revient à changer la valeur de p0 (pression au niveau de la mer) dans la formule utilisée par l'altimètre.

Pourquoi des recalages fréquents ?

Les randonneurs savent que certains jours, plus que d'autres, il faut sans cesse recaler l'altimètre en passant par des points d'altitude connue. Pour expliquer ces recalages systématiques, l'idée généralement admise est que la pression météorologique change et que cela perturbe les mesures. Ceci est vrai mais partiellement car c'est seulement l'une des raisons et non la seule. Cela est évident les jours où on effectue un seul calage, au début de la randonnée, au pied de la montagne. Arrivé au sommet, l'erreur de l'altimètre peut atteindre facilement une vingtaine de mètres, mais de retour au parking, l'altitude indiquée est à nouveau juste, montrant qu'il n'y a pas eu de variation de pression atmosphérique. L'erreur est à chercher ailleurs et provient essentiellement de l'influence de la température de l'air.

Influence de la variation de la pression météorologique

Sur l'ensemble d'une journée, il est rare que la pression météorologique change de plus de 2 ou 3 hPa. Cette variation cause des erreurs dans l'estimation de l'altitude d'une vingtaine de mètres environ, quelque soit le lieu où est effectuée la mesure.

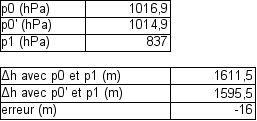
Par exemple, le calage de l'altimètre a été effectué le matin et, au moment où le randonneur veut connaître une altitude, la pression météorologique a augmenté de 2 hPa (sur toute la colonne d'air). L'altimètre calcule donc l'altitude du lieu avec une pression mesurée p1 , en utilisant une valeur de p0' trop basse de 2 hPa par rapport à la valeur réelle du moment. Pour le calcul, on utilise la pression mesurée le 14 novembre au col de Sommant (altitude 1611,5 m) p1 = 837 hPa alors que la pression au niveau de la mer valait p0 = 1016,9 hPa (valeur prise pour faire coïncider l'altitude). La pression p0' erronée est donc 1014,9 hPa.

L'erreur générée est de 16 m. En utilisant une autre pression p1, l'erreur serait quasiment identique.

Influence de la température réelle de l'air

Il ne s'agit pas ici de l'influence de la température de l'air sur le capteur (influence qui est corrigée puisque le capteur est compensé en température) mais de son influence sur la densité de l'air. La formule barométrique utilisée par l'altimètre suppose que la température au niveau de la mer est de 15°C et que le gradient ΔT est de 0,0065 K/m. Ceci n'est pratiquement jamais vrai et, par temps très chaud ou au contraire très froid, la formule introduit un biais systématique assez important.

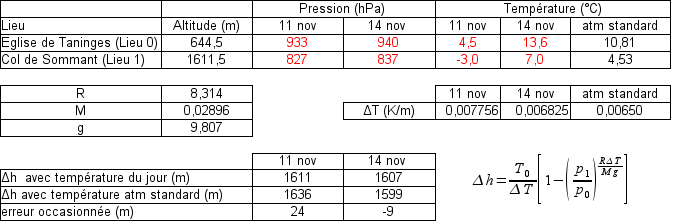
Par exemple, calculons la différence d'altitude entre le col de Sommant et l'église de Taninges avec les mesures de pression du 11 et du 14 novembre, soit en prenant les valeurs réelles de la température et du gradient, soit en prenant les valeurs de l'atmosphère standard. Nous considérons ces deux journées car, bien que très proches, les conditions météorologiques ont fortement varié (le 11 novembre est très froid alors que le 14 est très doux). Les températures à l'église de Taninges et au col de Sommant dans le cas de l'atmosphère standard sont calculées par : T(h) = T0 - ΔT x h = 15-0,0065 x h.

Le 11 novembre, la température réelle est plus froide que celle de l'atmosphère standard. L'air réel est donc plus dense que celui de l'atmosphère standard et la différence de pression correspond à une couche d'épaisseur plus faible que dans le cas de l'atmosphère standard : l'altimètre surestime largement l'altitude du col de Sommant. Le 14 novembre, la température réelle est plus chaude que celle de l'atmosphère standard. L'air réel est donc plus léger que celui de l'atmosphère standard et l'altimètre sous-estime l'altitude du col de Sommant. Les erreurs de l'altimètre dues à l'influence de la température de l'air sont d'autant plus grandes que les conditions s'éloignent des conditions standards et que la différence de pression observée est grande. En conclusion, l'influence de la température de l'air sur les erreurs d'un altimètre a donc autant d'importance, sinon plus, que les variations de la pression météorologique.

Influence du modèle d'atmosphère

Même si l'altimètre pouvait tenir compte de la température réelle de l'air, les calculs de l'altitude pourraient être faux dans certaines configurations météorologiques. Le modèle suppose une diminution linéaire de la température, ce qui n'est pas vrai par exemple par temps instable ou en hiver lors des inversions de température.

Conclusion

Même si la méthode barométrique, supplantée par les méthodes géodésiques et par les méthodes de positionnement par satellites, n'est plus utilisée aujourd'hui pour les nivellements de précision, elle reste néanmoins intéressante d'un point de vue pédagogique. Outre le fait qu'elle permet de réaliser très facilement des mesures en extérieur avec des élèves, elle est très formatrice pour la démarche scientifique : établissement des relations de départ et intégration de ces relations, élaboration d'un protocole de mesures (obligation de la simultanéité des mesures), attention à la précision des instruments et à la qualité des mesures (comment mesurer une température de l'air au sommet d'une montagne sujette aux bourrasques), et nécessité de prendre en compte des corrections multiples (influence de la température de l'air sur le capteur et sur la densité de l'air). En utilisant une simple montre altimètre, elle donne une différence d'altitude à une dizaine de mètres près.